Understanding Neural Coding on Latent Manifolds by Sharing Features and Dividing Ensembles

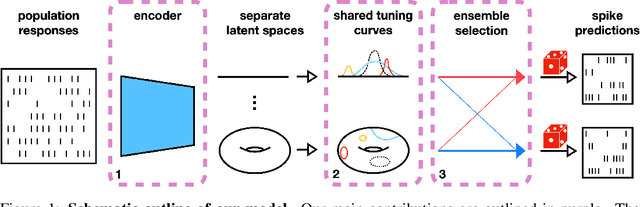
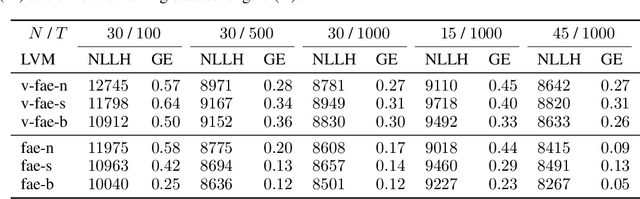
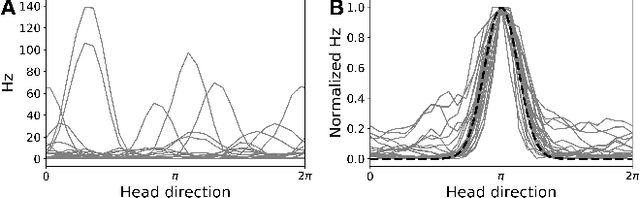
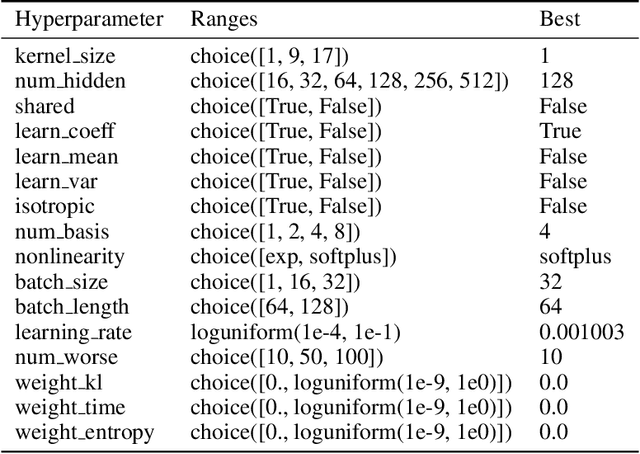
Systems neuroscience relies on two complementary views of neural data, characterized by single neuron tuning curves and analysis of population activity. These two perspectives combine elegantly in neural latent variable models that constrain the relationship between latent variables and neural activity, modeled by simple tuning curve functions. This has recently been demonstrated using Gaussian processes, with applications to realistic and topologically relevant latent manifolds. Those and previous models, however, missed crucial shared coding properties of neural populations. We propose feature sharing across neural tuning curves, which significantly improves performance and leads to better-behaved optimization. We also propose a solution to the problem of ensemble detection, whereby different groups of neurons, i.e., ensembles, can be modulated by different latent manifolds. This is achieved through a soft clustering of neurons during training, thus allowing for the separation of mixed neural populations in an unsupervised manner. These innovations lead to more interpretable models of neural population activity that train well and perform better even on mixtures of complex latent manifolds. Finally, we apply our method on a recently published grid cell dataset, recovering distinct ensembles, inferring toroidal latents and predicting neural tuning curves all in a single integrated modeling framework.

The Stochastic complexity of spin models: Are pairwise models really simple?

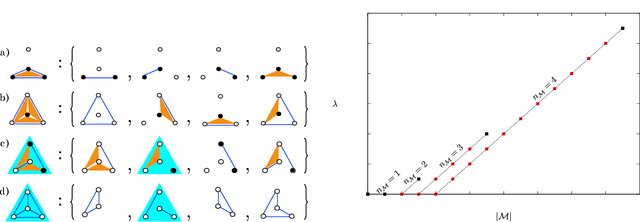
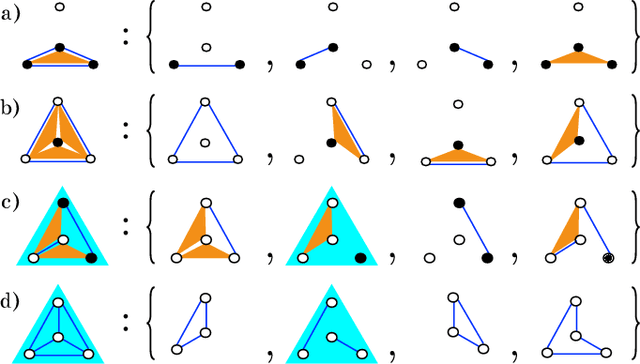
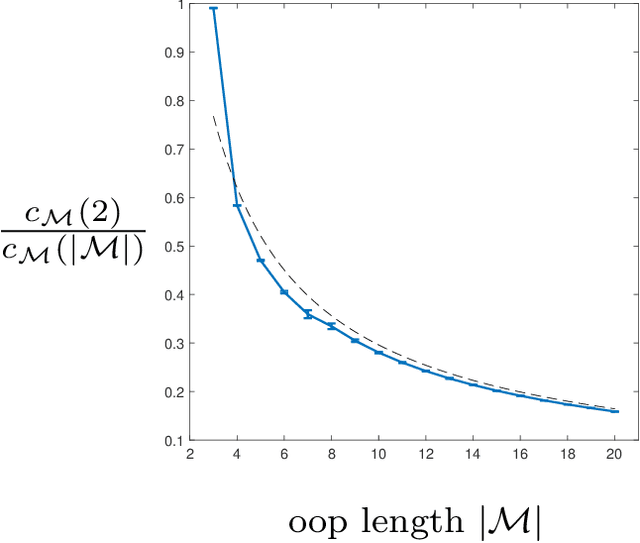
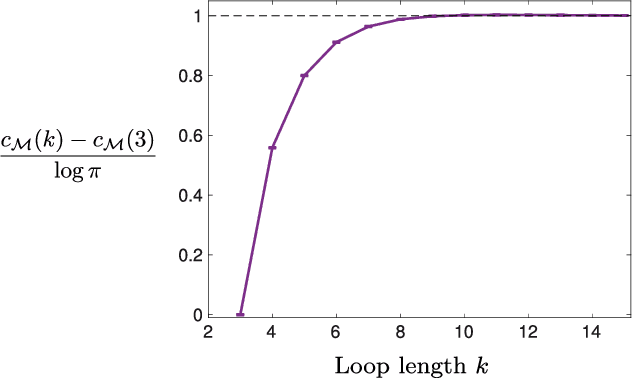
Models can be simple for different reasons: because they yield a simple and computationally efficient interpretation of a generic dataset (e.g. in terms of pairwise dependences) - as in statistical learning - or because they capture the essential ingredients of a specific phenomenon - as e.g. in physics - leading to non-trivial falsifiable predictions. In information theory and Bayesian inference, the simplicity of a model is precisely quantified in the stochastic complexity, which measures the number of bits needed to encode its parameters. In order to understand how simple models look like, we study the stochastic complexity of spin models with interactions of arbitrary order. We highlight the existence of invariances with respect to bijections within the space of operators, which allow us to partition the space of all models into equivalence classes, in which models share the same complexity. We thus found that the complexity (or simplicity) of a model is not determined by the order of the interactions, but rather by their mutual arrangements. Models where statistical dependencies are localized on non-overlapping groups of few variables (and that afford predictions on independencies that are easy to falsify) are simple. On the contrary, fully connected pairwise models, which are often used in statistical learning, appear to be highly complex, because of their extended set of interactions.

Variational perturbation and extended Plefka approaches to dynamics on random networks: the case of the kinetic Ising model

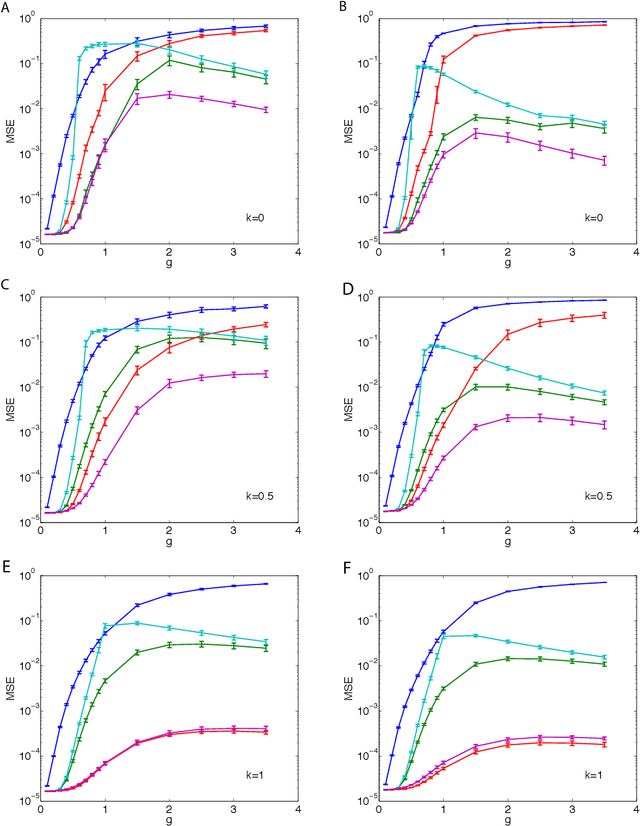
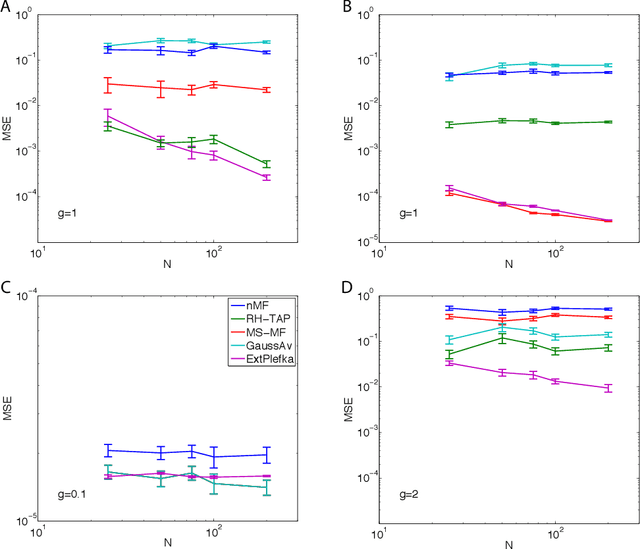
We describe and analyze some novel approaches for studying the dynamics of Ising spin glass models. We first briefly consider the variational approach based on minimizing the Kullback-Leibler divergence between independent trajectories and the real ones and note that this approach only coincides with the mean field equations from the saddle point approximation to the generating functional when the dynamics is defined through a logistic link function, which is the case for the kinetic Ising model with parallel update. We then spend the rest of the paper developing two ways of going beyond the saddle point approximation to the generating functional. In the first one, we develop a variational perturbative approximation to the generating functional by expanding the action around a quadratic function of the local fields and conjugate local fields whose parameters are optimized. We derive analytical expressions for the optimal parameters and show that when the optimization is suitably restricted, we recover the mean field equations that are exact for the fully asymmetric random couplings (M\'ezard and Sakellariou, 2011). However, without this restriction the results are different. We also describe an extended Plefka expansion in which in addition to the magnetization, we also fix the correlation and response functions. Finally, we numerically study the performance of these approximations for Sherrington-Kirkpatrick type couplings for various coupling strengths, degrees of coupling symmetry and external fields. We show that the dynamical equations derived from the extended Plefka expansion outperform the others in all regimes, although it is computationally more demanding. The unconstrained variational approach does not perform well in the small coupling regime, while it approaches dynamical TAP equations of (Roudi and Hertz, 2011) for strong couplings.