Understanding Neural Coding on Latent Manifolds by Sharing Features and Dividing Ensembles

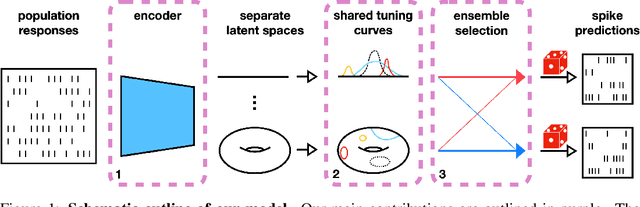
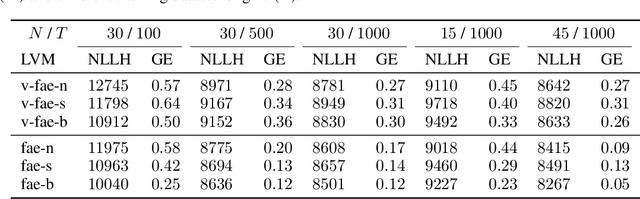
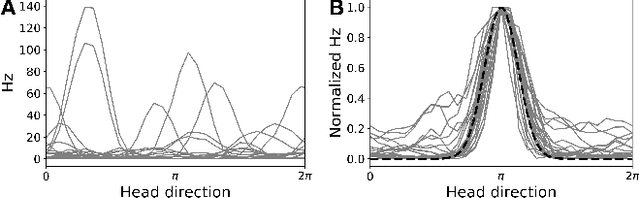
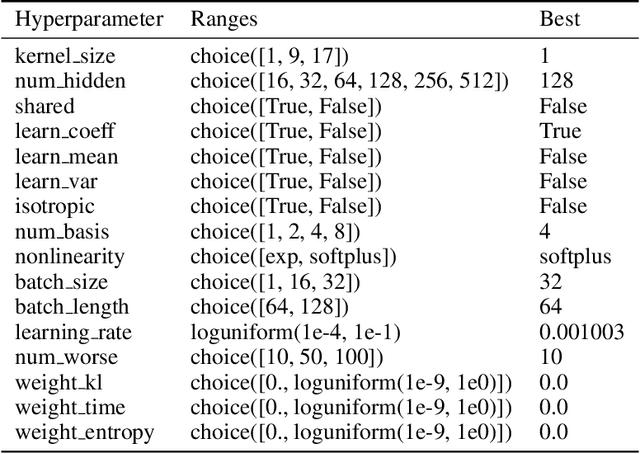
Systems neuroscience relies on two complementary views of neural data, characterized by single neuron tuning curves and analysis of population activity. These two perspectives combine elegantly in neural latent variable models that constrain the relationship between latent variables and neural activity, modeled by simple tuning curve functions. This has recently been demonstrated using Gaussian processes, with applications to realistic and topologically relevant latent manifolds. Those and previous models, however, missed crucial shared coding properties of neural populations. We propose feature sharing across neural tuning curves, which significantly improves performance and leads to better-behaved optimization. We also propose a solution to the problem of ensemble detection, whereby different groups of neurons, i.e., ensembles, can be modulated by different latent manifolds. This is achieved through a soft clustering of neurons during training, thus allowing for the separation of mixed neural populations in an unsupervised manner. These innovations lead to more interpretable models of neural population activity that train well and perform better even on mixtures of complex latent manifolds. Finally, we apply our method on a recently published grid cell dataset, recovering distinct ensembles, inferring toroidal latents and predicting neural tuning curves all in a single integrated modeling framework.