The Stochastic complexity of spin models: Are pairwise models really simple?

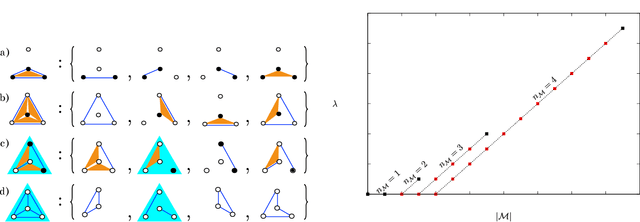
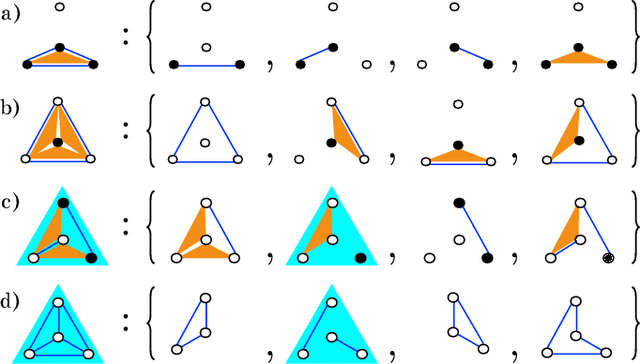
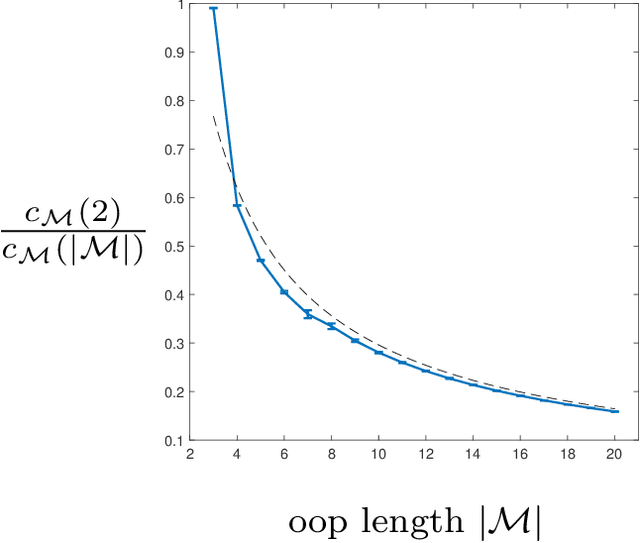
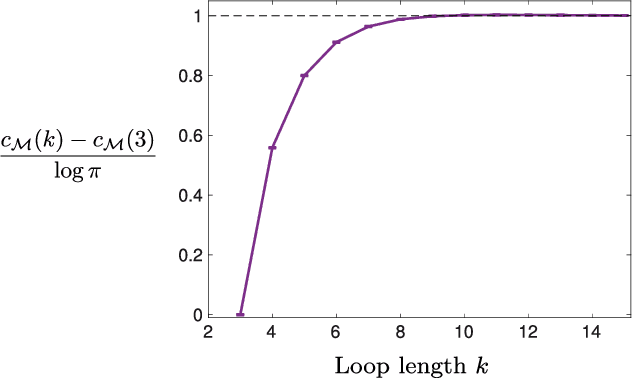
Models can be simple for different reasons: because they yield a simple and computationally efficient interpretation of a generic dataset (e.g. in terms of pairwise dependences) - as in statistical learning - or because they capture the essential ingredients of a specific phenomenon - as e.g. in physics - leading to non-trivial falsifiable predictions. In information theory and Bayesian inference, the simplicity of a model is precisely quantified in the stochastic complexity, which measures the number of bits needed to encode its parameters. In order to understand how simple models look like, we study the stochastic complexity of spin models with interactions of arbitrary order. We highlight the existence of invariances with respect to bijections within the space of operators, which allow us to partition the space of all models into equivalence classes, in which models share the same complexity. We thus found that the complexity (or simplicity) of a model is not determined by the order of the interactions, but rather by their mutual arrangements. Models where statistical dependencies are localized on non-overlapping groups of few variables (and that afford predictions on independencies that are easy to falsify) are simple. On the contrary, fully connected pairwise models, which are often used in statistical learning, appear to be highly complex, because of their extended set of interactions.