Multiscale Relevance of Natural Images

We use an agnostic information-theoretic approach to investigate the statistical properties of natural images. We introduce the Multiscale Relevance (MSR) measure to assess the robustness of images to compression at all scales. Starting in a controlled environment, we characterize the MSR of synthetic random textures as function of image roughness H and other relevant parameters. We then extend the analysis to natural images and find striking similarities with critical (H = 0) random textures. We show that the MSR is more robust and informative of image content than classical methods such as power spectrum analysis. Finally, we confront the MSR to classical measures for the calibration of common procedures such as color mapping and denoising. Overall, the MSR approach appears to be a good candidate for advanced image analysis and image processing, while providing a good level of physical interpretability.

The Stochastic complexity of spin models: Are pairwise models really simple?

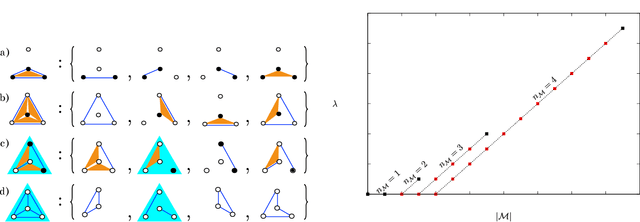
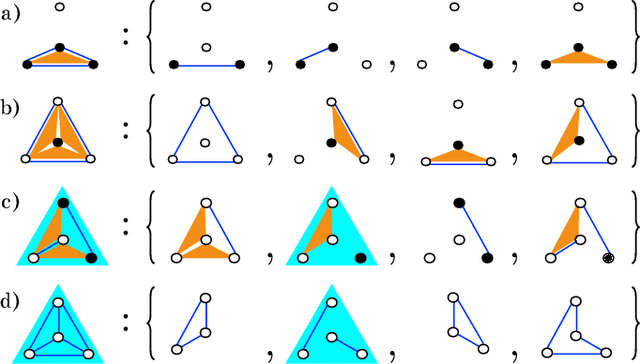
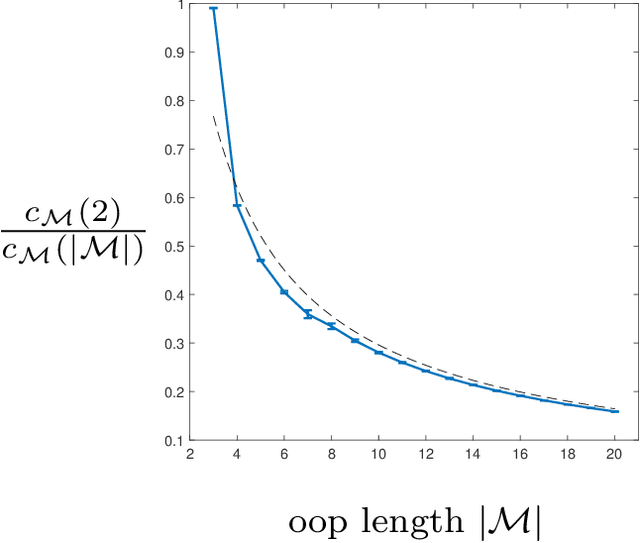
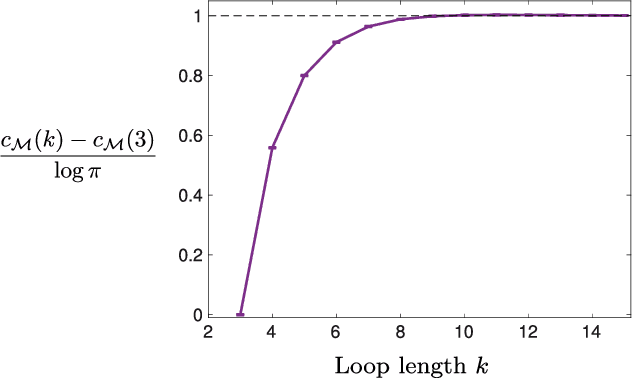
Models can be simple for different reasons: because they yield a simple and computationally efficient interpretation of a generic dataset (e.g. in terms of pairwise dependences) - as in statistical learning - or because they capture the essential ingredients of a specific phenomenon - as e.g. in physics - leading to non-trivial falsifiable predictions. In information theory and Bayesian inference, the simplicity of a model is precisely quantified in the stochastic complexity, which measures the number of bits needed to encode its parameters. In order to understand how simple models look like, we study the stochastic complexity of spin models with interactions of arbitrary order. We highlight the existence of invariances with respect to bijections within the space of operators, which allow us to partition the space of all models into equivalence classes, in which models share the same complexity. We thus found that the complexity (or simplicity) of a model is not determined by the order of the interactions, but rather by their mutual arrangements. Models where statistical dependencies are localized on non-overlapping groups of few variables (and that afford predictions on independencies that are easy to falsify) are simple. On the contrary, fully connected pairwise models, which are often used in statistical learning, appear to be highly complex, because of their extended set of interactions.

Uncovering Causality from Multivariate Hawkes Integrated Cumulants

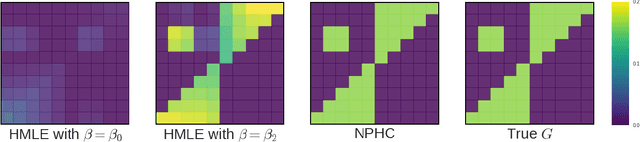
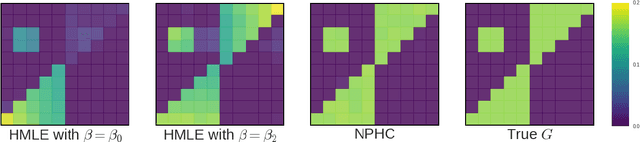
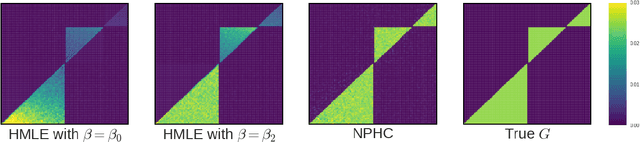
We design a new nonparametric method that allows one to estimate the matrix of integrated kernels of a multivariate Hawkes process. This matrix not only encodes the mutual influences of each nodes of the process, but also disentangles the causality relationships between them. Our approach is the first that leads to an estimation of this matrix without any parametric modeling and estimation of the kernels themselves. A consequence is that it can give an estimation of causality relationships between nodes (or users), based on their activity timestamps (on a social network for instance), without knowing or estimating the shape of the activities lifetime. For that purpose, we introduce a moment matching method that fits the third-order integrated cumulants of the process. We show on numerical experiments that our approach is indeed very robust to the shape of the kernels, and gives appealing results on the MemeTracker database.

Mean-field inference of Hawkes point processes

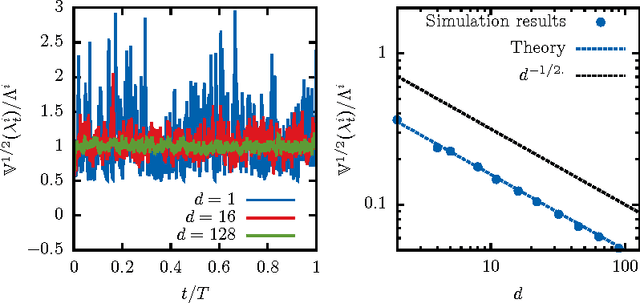
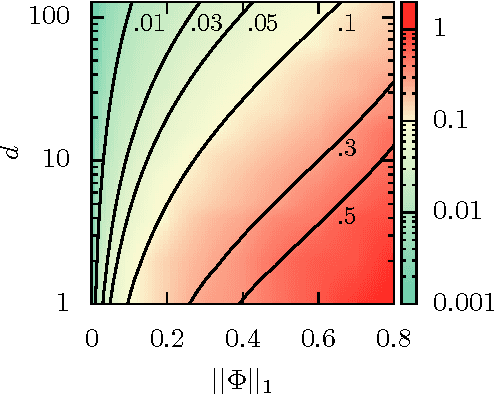
We propose a fast and efficient estimation method that is able to accurately recover the parameters of a d-dimensional Hawkes point-process from a set of observations. We exploit a mean-field approximation that is valid when the fluctuations of the stochastic intensity are small. We show that this is notably the case in situations when interactions are sufficiently weak, when the dimension of the system is high or when the fluctuations are self-averaging due to the large number of past events they involve. In such a regime the estimation of a Hawkes process can be mapped on a least-squares problem for which we provide an analytic solution. Though this estimator is biased, we show that its precision can be comparable to the one of the Maximum Likelihood Estimator while its computation speed is shown to be improved considerably. We give a theoretical control on the accuracy of our new approach and illustrate its efficiency using synthetic datasets, in order to assess the statistical estimation error of the parameters.