Forecasting threshold exceedance of atmospheric variables at a specific location

This study compares two methodological approaches for predicting, at a given site, threshold exceedances of atmospheric variables such as temperature and wind speed: (i) direct probabilistic methods, which treat exceedance as a binary classification problem, and (ii) full distribution probabilistic methods, which model the complete conditional probability law of the target variable. Using theoretical analysis and numerical simulations on a toy model, alongside real-world data from the MeteoNet dataset (2016--2018) for southeastern France, we demonstrate that the full distribution approach consistently outperforms the direct method for rare, extreme events. This advantage arises because the full distribution approach effectively learns the parameters of the conditional distribution from moderate and mild intensity events, thereby achieving better calibration and discrimination in the tails. We find that the specific parametric shape of the chosen distribution plays a secondary role compared to accurately capturing predictable shifts in its bulk properties (i.e., mean and variance). This empirical indistinguishability is also informative about the physical mechanics driving atmospheric extremes, suggesting that extreme exceedances are primarily driven by significant conditional displacements of the entire distribution rather than by unpredictable, fat-tailed anomalies within a static climatology. Our results are validated for both strong surface wind speeds and intense hourly rainfall, with performance evaluated using proper scoring rules (Brier score, logarithmic score) and deterministic skill scores (Peirce Skill Score, CSI, HSS). These findings highlight the critical importance of modeling the full probability distribution for rare-event forecasting and provide practical guidance for improving extreme weather prediction in operational meteorology.

Agent market orders representation through a contrastive learning approach

Due to the access to the labeled orders on the CAC40 data from Euronext, we are able to analyse agents' behaviours in the market based on their placed orders. In this study, we construct a self-supervised learning model using triplet loss to effectively learn the representation of agent market orders. By acquiring this learned representation, various downstream tasks become feasible. In this work, we utilise the K-means clustering algorithm on the learned representation vectors of agent orders to identify distinct behaviour types within each cluster.

Concentration for matrix martingales in continuous time and microscopic activity of social networks

This paper gives new concentration inequalities for the spectral norm of a wide class of matrix martingales in continuous time. These results extend previously established Freedman and Bernstein inequalities for series of random matrices to the class of continuous time processes. Our analysis relies on a new supermartingale property of the trace exponential proved within the framework of stochastic calculus. We provide also several examples that illustrate the fact that our results allow us to recover easily several formerly obtained sharp bounds for discrete time matrix martingales.

Mean-field inference of Hawkes point processes

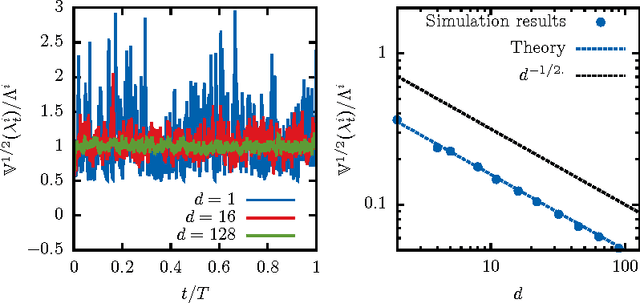
We propose a fast and efficient estimation method that is able to accurately recover the parameters of a d-dimensional Hawkes point-process from a set of observations. We exploit a mean-field approximation that is valid when the fluctuations of the stochastic intensity are small. We show that this is notably the case in situations when interactions are sufficiently weak, when the dimension of the system is high or when the fluctuations are self-averaging due to the large number of past events they involve. In such a regime the estimation of a Hawkes process can be mapped on a least-squares problem for which we provide an analytic solution. Though this estimator is biased, we show that its precision can be comparable to the one of the Maximum Likelihood Estimator while its computation speed is shown to be improved considerably. We give a theoretical control on the accuracy of our new approach and illustrate its efficiency using synthetic datasets, in order to assess the statistical estimation error of the parameters.

A generalization error bound for sparse and low-rank multivariate Hawkes processes

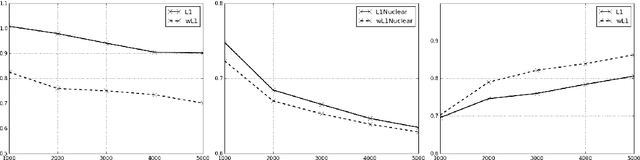
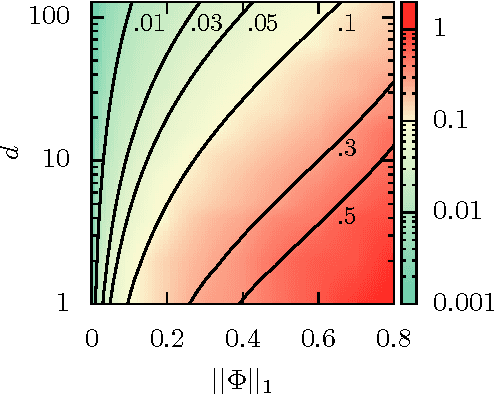
We consider the problem of unveiling the implicit network structure of user interactions in a social network, based only on high-frequency timestamps. Our inference is based on the minimization of the least-squares loss associated with a multivariate Hawkes model, penalized by $\ell_1$ and trace norms. We provide a first theoretical analysis of the generalization error for this problem, that includes sparsity and low-rank inducing priors. This result involves a new data-driven concentration inequality for matrix martingales in continuous time with observable variance, which is a result of independent interest. A consequence of our analysis is the construction of sharply tuned $\ell_1$ and trace-norm penalizations, that leads to a data-driven scaling of the variability of information available for each users. Numerical experiments illustrate the strong improvements achieved by the use of such data-driven penalizations.