Robust Stochastic Optimization via Gradient Quantile Clipping

We introduce a clipping strategy for Stochastic Gradient Descent (SGD) which uses quantiles of the gradient norm as clipping thresholds. We prove that this new strategy provides a robust and efficient optimization algorithm for smooth objectives (convex or non-convex), that tolerates heavy-tailed samples (including infinite variance) and a fraction of outliers in the data stream akin to Huber contamination. Our mathematical analysis leverages the connection between constant step size SGD and Markov chains and handles the bias introduced by clipping in an original way. For strongly convex objectives, we prove that the iteration converges to a concentrated distribution and derive high probability bounds on the final estimation error. In the non-convex case, we prove that the limit distribution is localized on a neighborhood with low gradient. We propose an implementation of this algorithm using rolling quantiles which leads to a highly efficient optimization procedure with strong robustness properties, as confirmed by our numerical experiments.

Online Inventory Problems: Beyond the i.i.d. Setting with Online Convex Optimization

We study multi-product inventory control problems where a manager makes sequential replenishment decisions based on partial historical information in order to minimize its cumulative losses. Our motivation is to consider general demands, losses and dynamics to go beyond standard models which usually rely on newsvendor-type losses, fixed dynamics, and unrealistic i.i.d. demand assumptions. We propose MaxCOSD, an online algorithm that has provable guarantees even for problems with non-i.i.d. demands and stateful dynamics, including for instance perishability. We consider what we call non-degeneracy assumptions on the demand process, and argue that they are necessary to allow learning.

Convergence and concentration properties of constant step-size SGD through Markov chains

We consider the optimization of a smooth and strongly convex objective using constant step-size stochastic gradient descent (SGD) and study its properties through the prism of Markov chains. We show that, for unbiased gradient estimates with mildly controlled variance, the iteration converges to an invariant distribution in total variation distance. We also establish this convergence in Wasserstein-2 distance in a more general setting compared to previous work. Thanks to the invariance property of the limit distribution, our analysis shows that the latter inherits sub-Gaussian or sub-exponential concentration properties when these hold true for the gradient. This allows the derivation of high-confidence bounds for the final estimate. Finally, under such conditions in the linear case, we obtain a dimension-free deviation bound for the Polyak-Ruppert average of a tail sequence. All our results are non-asymptotic and their consequences are discussed through a few applications.

Robust methods for high-dimensional linear learning

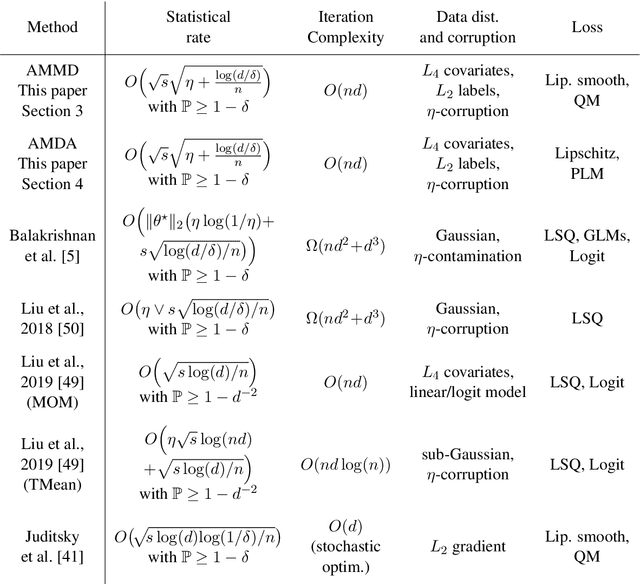
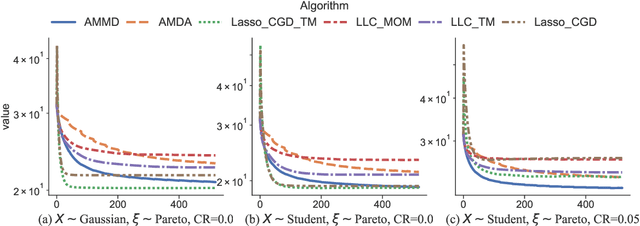
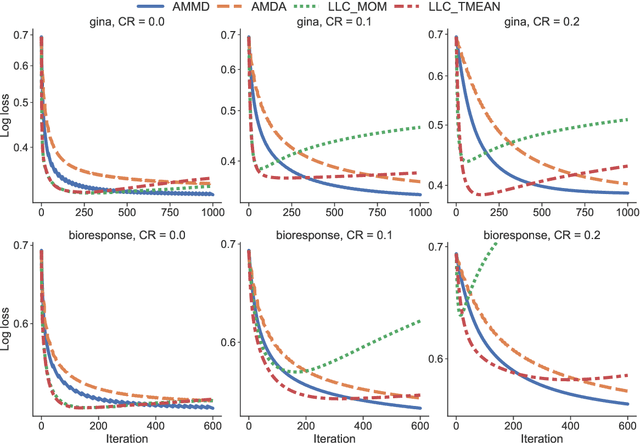
We propose statistically robust and computationally efficient linear learning methods in the high-dimensional batch setting, where the number of features $d$ may exceed the sample size $n$. We employ, in a generic learning setting, two algorithms depending on whether the considered loss function is gradient-Lipschitz or not. Then, we instantiate our framework on several applications including vanilla sparse, group-sparse and low-rank matrix recovery. This leads, for each application, to efficient and robust learning algorithms, that reach near-optimal estimation rates under heavy-tailed distributions and the presence of outliers. For vanilla $s$-sparsity, we are able to reach the $s\log (d)/n$ rate under heavy-tails and $\eta$-corruption, at a computational cost comparable to that of non-robust analogs. We provide an efficient implementation of our algorithms in an open-source $\mathtt{Python}$ library called $\mathtt{linlearn}$, by means of which we carry out numerical experiments which confirm our theoretical findings together with a comparison to other recent approaches proposed in the literature.

Robust supervised learning with coordinate gradient descent

This paper considers the problem of supervised learning with linear methods when both features and labels can be corrupted, either in the form of heavy tailed data and/or corrupted rows. We introduce a combination of coordinate gradient descent as a learning algorithm together with robust estimators of the partial derivatives. This leads to robust statistical learning methods that have a numerical complexity nearly identical to non-robust ones based on empirical risk minimization. The main idea is simple: while robust learning with gradient descent requires the computational cost of robustly estimating the whole gradient to update all parameters, a parameter can be updated immediately using a robust estimator of a single partial derivative in coordinate gradient descent. We prove upper bounds on the generalization error of the algorithms derived from this idea, that control both the optimization and statistical errors with and without a strong convexity assumption of the risk. Finally, we propose an efficient implementation of this approach in a new python library called linlearn, and demonstrate through extensive numerical experiments that our approach introduces a new interesting compromise between robustness, statistical performance and numerical efficiency for this problem.

WildWood: a new Random Forest algorithm

We introduce WildWood (WW), a new ensemble algorithm for supervised learning of Random Forest (RF) type. While standard RF algorithms use bootstrap out-of-bag samples to compute out-of-bag scores, WW uses these samples to produce improved predictions given by an aggregation of the predictions of all possible subtrees of each fully grown tree in the forest. This is achieved by aggregation with exponential weights computed over out-of-bag samples, that are computed exactly and very efficiently thanks to an algorithm called context tree weighting. This improvement, combined with a histogram strategy to accelerate split finding, makes WW fast and competitive compared with other well-established ensemble methods, such as standard RF and extreme gradient boosting algorithms.

About contrastive unsupervised representation learning for classification and its convergence

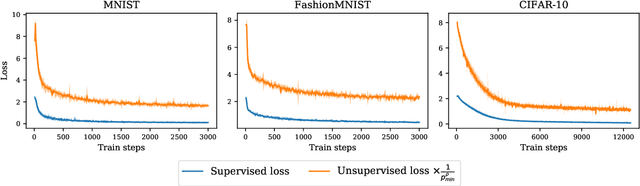
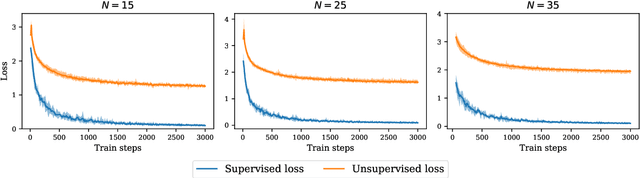
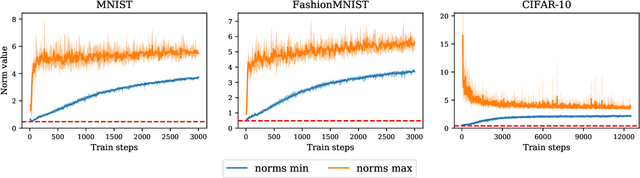
Contrastive representation learning has been recently proved to be very efficient for self-supervised training. These methods have been successfully used to train encoders which perform comparably to supervised training on downstream classification tasks. A few works have started to build a theoretical framework around contrastive learning in which guarantees for its performance can be proven. We provide extensions of these results to training with multiple negative samples and for multiway classification. Furthermore, we provide convergence guarantees for the minimization of the contrastive training error with gradient descent of an overparametrized deep neural encoder, and provide some numerical experiments that complement our theoretical findings

An improper estimator with optimal excess risk in misspecified density estimation and logistic regression

We introduce a procedure for predictive conditional density estimation under logarithmic loss, which we call SMP (Sample Minmax Predictor). This predictor minimizes a new general excess risk bound, which critically remains valid under model misspecification. On standard examples, this bound scales as $d/n$ where $d$ is the dimension of the model and $n$ the sample size, regardless of the true distribution. The SMP, which is an improper (out-of-model) procedure, improves over proper (within-model) estimators (such as the maximum likelihood estimator), whose excess risk can degrade arbitrarily in the misspecified case. For density estimation, our bounds improve over approaches based on online-to-batch conversion, by removing suboptimal $\log n$ factors, addressing an open problem from Gr{\"u}nwald and Kot{\l}owski (2011) for the considered models. For the Gaussian linear model, the SMP admits an explicit expression, and its expected excess risk in the general misspecified case is at most twice the minimax excess risk in the \emph{well-specified case}, but without any condition on the noise variance or approximation error of the linear model. For logistic regression, a penalized SMP can be computed efficiently by training two logistic regressions, and achieves a non-asymptotic excess risk of $O((d + B^2R^2)/n)$, where $R$ is a bound on the norm of the features and $B$ the norm of the comparison linear predictor. This improves the rates of proper (within-model) estimators, since such procedures can achieve no better rate than $\min(BR/\sqrt{n},de^{BR}/n)$ in general. This also provides a computationally more efficient alternative to approaches based on online-to-batch conversion of Bayesian mixture procedures, which require approximate posterior sampling, thereby partly answering a question by Foster et al. (2018).

ZiMM: a deep learning model for long term adverse events with non-clinical claims data

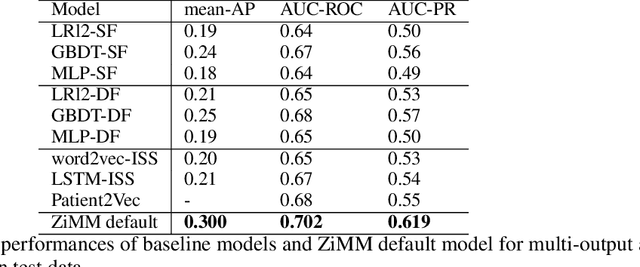
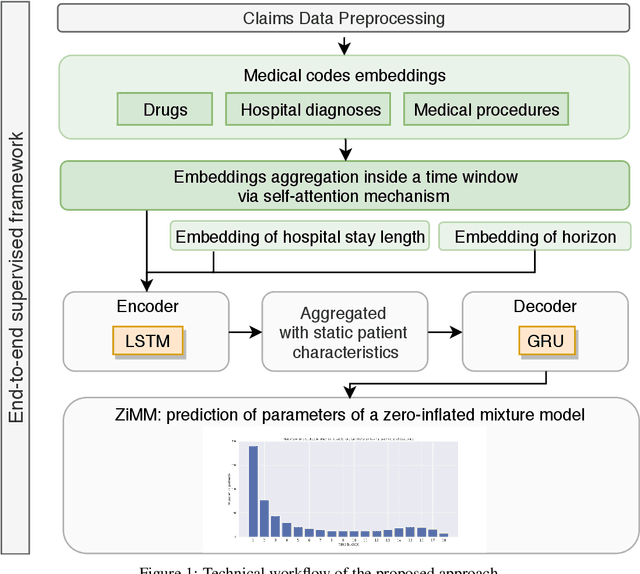
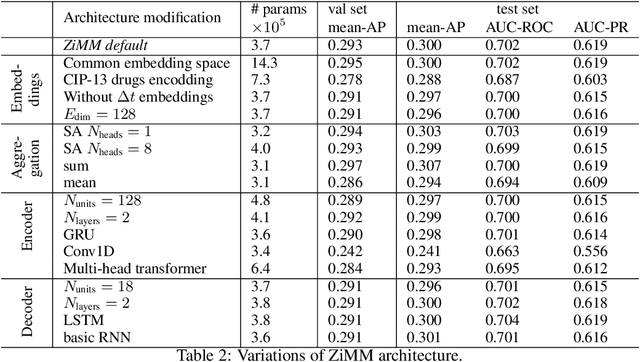
This paper considers the problem of modeling long-term adverse events following prostatic surgery performed on patients with urination problems, using the French national health insurance database (SNIIRAM), which is a non-clinical claims database built around healthcare reimbursements of more than 65 million people. This makes the problem particularly challenging compared to what could be done using clinical hospital data, albeit a much smaller sample, while we exploit here the claims of almost all French citizens diagnosed with prostatic problems (with between 1.5 and 5 years of history). We introduce a new model, called ZiMM (Zero-inflated Mixture of Multinomial distributions) to capture such long-term adverse events, and we build a deep-learning architecture on top of it to deal with the complex, highly heterogeneous and sparse patterns observable in such a large claims database. This architecture combines several ingredients: embedding layers for drugs, medical procedures, and diagnosis codes; embeddings aggregation through a self-attention mechanism; recurrent layers to encode the health pathways of patients before their surgery and a final decoder layer which outputs the ZiMM's parameters.

AMF: Aggregated Mondrian Forests for Online Learning

Random Forests (RF) is one of the algorithms of choice in many supervised learning applications, be it classification or regression. The appeal of such methods comes from a combination of several characteristics: a remarkable accuracy in a variety of tasks, a small number of parameters to tune, robustness with respect to features scaling, a reasonable computational cost for training and prediction, and their suitability in high-dimensional settings. The most commonly used RF variants however are "offline" algorithms, which require the availability of the whole dataset at once. In this paper, we introduce AMF, an online random forest algorithm based on Mondrian Forests. Using a variant of the Context Tree Weighting algorithm, we show that it is possible to efficiently perform an exact aggregation over all prunings of the trees; in particular, this enables to obtain a truly online parameter-free algorithm which is competitive with the optimal pruning of the Mondrian tree, and thus adaptive to the unknown regularity of the regression function. Numerical experiments show that AMF is competitive with respect to several strong baselines on a large number of datasets for multi-class classification.