Language verY Rare for All

In the quest to overcome language barriers, encoder-decoder models like NLLB have expanded machine translation to rare languages, with some models (e.g., NLLB 1.3B) even trainable on a single GPU. While general-purpose LLMs perform well in translation, open LLMs prove highly competitive when fine-tuned for specific tasks involving unknown corpora. We introduce LYRA (Language verY Rare for All), a novel approach that combines open LLM fine-tuning, retrieval-augmented generation (RAG), and transfer learning from related high-resource languages. This study is exclusively focused on single-GPU training to facilitate ease of adoption. Our study focuses on two-way translation between French and Mon\'egasque, a rare language unsupported by existing translation tools due to limited corpus availability. Our results demonstrate LYRA's effectiveness, frequently surpassing and consistently matching state-of-the-art encoder-decoder models in rare language translation.

Robust Stochastic Optimization via Gradient Quantile Clipping

We introduce a clipping strategy for Stochastic Gradient Descent (SGD) which uses quantiles of the gradient norm as clipping thresholds. We prove that this new strategy provides a robust and efficient optimization algorithm for smooth objectives (convex or non-convex), that tolerates heavy-tailed samples (including infinite variance) and a fraction of outliers in the data stream akin to Huber contamination. Our mathematical analysis leverages the connection between constant step size SGD and Markov chains and handles the bias introduced by clipping in an original way. For strongly convex objectives, we prove that the iteration converges to a concentrated distribution and derive high probability bounds on the final estimation error. In the non-convex case, we prove that the limit distribution is localized on a neighborhood with low gradient. We propose an implementation of this algorithm using rolling quantiles which leads to a highly efficient optimization procedure with strong robustness properties, as confirmed by our numerical experiments.

Convergence and concentration properties of constant step-size SGD through Markov chains

We consider the optimization of a smooth and strongly convex objective using constant step-size stochastic gradient descent (SGD) and study its properties through the prism of Markov chains. We show that, for unbiased gradient estimates with mildly controlled variance, the iteration converges to an invariant distribution in total variation distance. We also establish this convergence in Wasserstein-2 distance in a more general setting compared to previous work. Thanks to the invariance property of the limit distribution, our analysis shows that the latter inherits sub-Gaussian or sub-exponential concentration properties when these hold true for the gradient. This allows the derivation of high-confidence bounds for the final estimate. Finally, under such conditions in the linear case, we obtain a dimension-free deviation bound for the Polyak-Ruppert average of a tail sequence. All our results are non-asymptotic and their consequences are discussed through a few applications.

Robust methods for high-dimensional linear learning

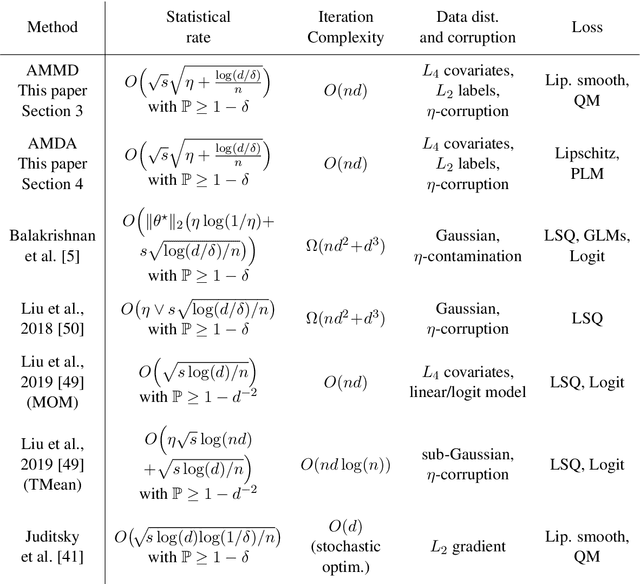
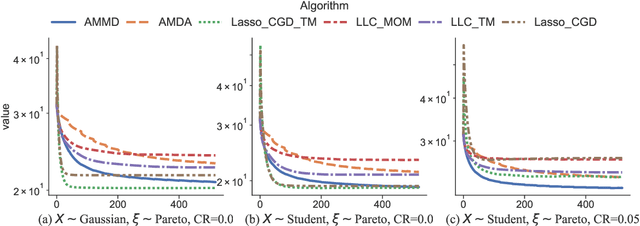
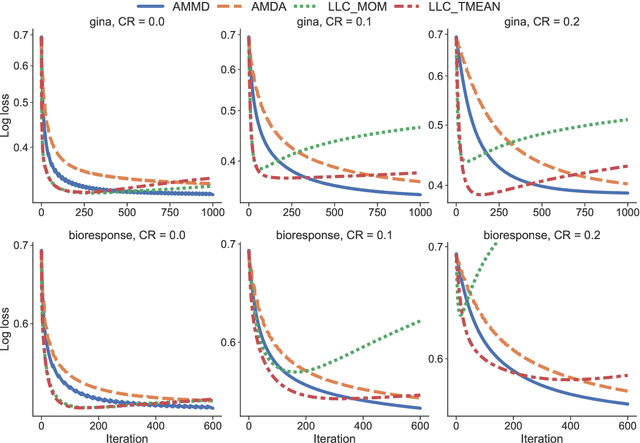
We propose statistically robust and computationally efficient linear learning methods in the high-dimensional batch setting, where the number of features $d$ may exceed the sample size $n$. We employ, in a generic learning setting, two algorithms depending on whether the considered loss function is gradient-Lipschitz or not. Then, we instantiate our framework on several applications including vanilla sparse, group-sparse and low-rank matrix recovery. This leads, for each application, to efficient and robust learning algorithms, that reach near-optimal estimation rates under heavy-tailed distributions and the presence of outliers. For vanilla $s$-sparsity, we are able to reach the $s\log (d)/n$ rate under heavy-tails and $\eta$-corruption, at a computational cost comparable to that of non-robust analogs. We provide an efficient implementation of our algorithms in an open-source $\mathtt{Python}$ library called $\mathtt{linlearn}$, by means of which we carry out numerical experiments which confirm our theoretical findings together with a comparison to other recent approaches proposed in the literature.

Robust supervised learning with coordinate gradient descent

This paper considers the problem of supervised learning with linear methods when both features and labels can be corrupted, either in the form of heavy tailed data and/or corrupted rows. We introduce a combination of coordinate gradient descent as a learning algorithm together with robust estimators of the partial derivatives. This leads to robust statistical learning methods that have a numerical complexity nearly identical to non-robust ones based on empirical risk minimization. The main idea is simple: while robust learning with gradient descent requires the computational cost of robustly estimating the whole gradient to update all parameters, a parameter can be updated immediately using a robust estimator of a single partial derivative in coordinate gradient descent. We prove upper bounds on the generalization error of the algorithms derived from this idea, that control both the optimization and statistical errors with and without a strong convexity assumption of the risk. Finally, we propose an efficient implementation of this approach in a new python library called linlearn, and demonstrate through extensive numerical experiments that our approach introduces a new interesting compromise between robustness, statistical performance and numerical efficiency for this problem.

WildWood: a new Random Forest algorithm

We introduce WildWood (WW), a new ensemble algorithm for supervised learning of Random Forest (RF) type. While standard RF algorithms use bootstrap out-of-bag samples to compute out-of-bag scores, WW uses these samples to produce improved predictions given by an aggregation of the predictions of all possible subtrees of each fully grown tree in the forest. This is achieved by aggregation with exponential weights computed over out-of-bag samples, that are computed exactly and very efficiently thanks to an algorithm called context tree weighting. This improvement, combined with a histogram strategy to accelerate split finding, makes WW fast and competitive compared with other well-established ensemble methods, such as standard RF and extreme gradient boosting algorithms.

About contrastive unsupervised representation learning for classification and its convergence

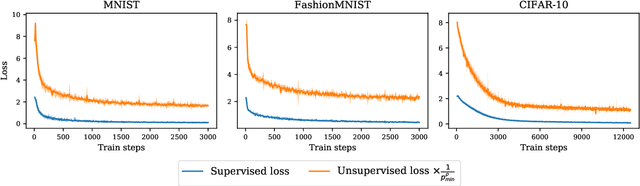
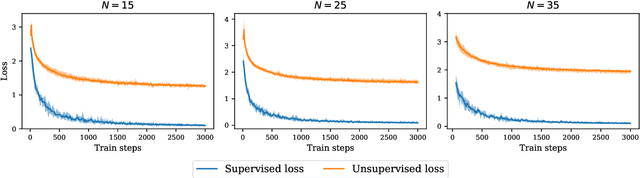
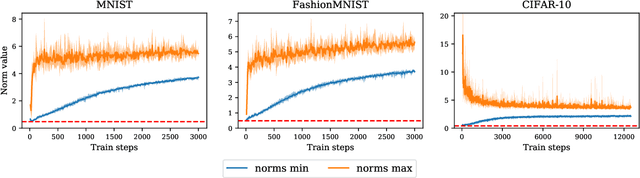
Contrastive representation learning has been recently proved to be very efficient for self-supervised training. These methods have been successfully used to train encoders which perform comparably to supervised training on downstream classification tasks. A few works have started to build a theoretical framework around contrastive learning in which guarantees for its performance can be proven. We provide extensions of these results to training with multiple negative samples and for multiway classification. Furthermore, we provide convergence guarantees for the minimization of the contrastive training error with gradient descent of an overparametrized deep neural encoder, and provide some numerical experiments that complement our theoretical findings