Erwan Scornet
LPSM
Principled Federated Random Forests for Heterogeneous Data
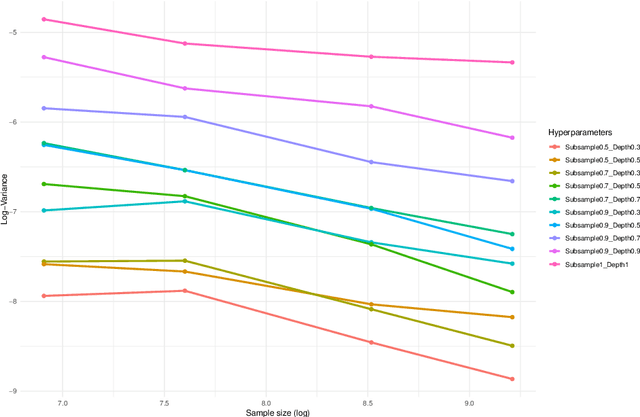
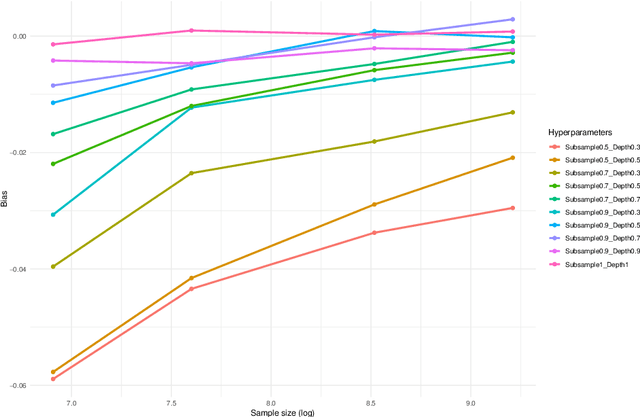
Feb 03, 2026Abstract:Random Forests (RF) are among the most powerful and widely used predictive models for centralized tabular data, yet few methods exist to adapt them to the federated learning setting. Unlike most federated learning approaches, the piecewise-constant nature of RF prevents exact gradient-based optimization. As a result, existing federated RF implementations rely on unprincipled heuristics: for instance, aggregating decision trees trained independently on clients fails to optimize the global impurity criterion, even under simple distribution shifts. We propose FedForest, a new federated RF algorithm for horizontally partitioned data that naturally accommodates diverse forms of client data heterogeneity, from covariate shift to more complex outcome shift mechanisms. We prove that our splitting procedure, based on aggregating carefully chosen client statistics, closely approximates the split selected by a centralized algorithm. Moreover, FedForest allows splits on client indicators, enabling a non-parametric form of personalization that is absent from prior federated random forest methods. Empirically, we demonstrate that the resulting federated forests closely match centralized performance across heterogeneous benchmarks while remaining communication-efficient.
Privacy Amplification by Missing Data
Feb 02, 2026Abstract:Privacy preservation is a fundamental requirement in many high-stakes domains such as medicine and finance, where sensitive personal data must be analyzed without compromising individual confidentiality. At the same time, these applications often involve datasets with missing values due to non-response, data corruption, or deliberate anonymization. Missing data is traditionally viewed as a limitation because it reduces the information available to analysts and can degrade model performance. In this work, we take an alternative perspective and study missing data from a privacy preservation standpoint. Intuitively, when features are missing, less information is revealed about individuals, suggesting that missingness could inherently enhance privacy. We formalize this intuition by analyzing missing data as a privacy amplification mechanism within the framework of differential privacy. We show, for the first time, that incomplete data can yield privacy amplification for differentially private algorithms.
When Pattern-by-Pattern Works: Theoretical and Empirical Insights for Logistic Models with Missing Values
Jul 17, 2025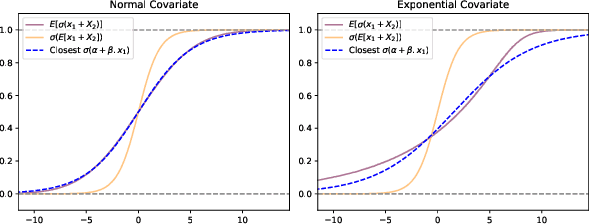
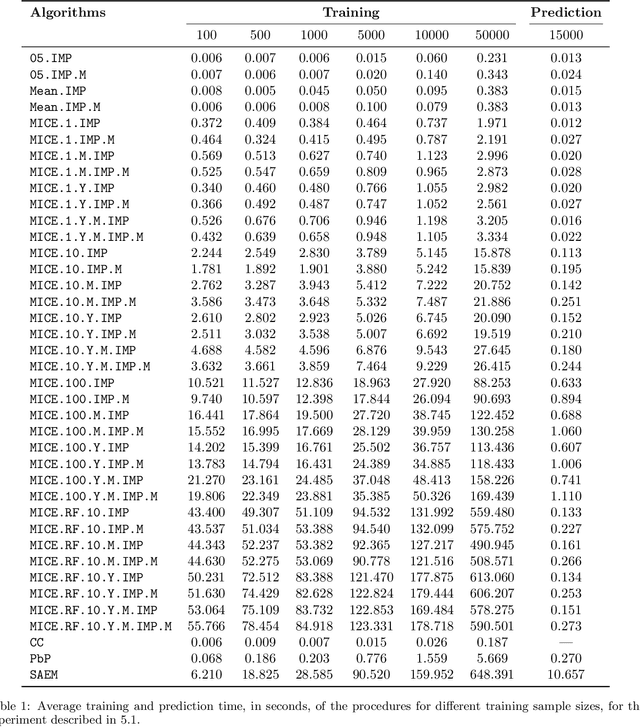
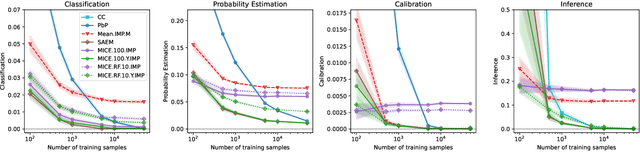
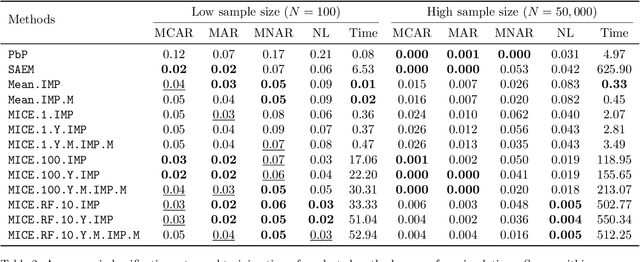
Abstract:Predicting a response with partially missing inputs remains a challenging task even in parametric models, since parameter estimation in itself is not sufficient to predict on partially observed inputs. Several works study prediction in linear models. In this paper, we focus on logistic models, which present their own difficulties. From a theoretical perspective, we prove that a Pattern-by-Pattern strategy (PbP), which learns one logistic model per missingness pattern, accurately approximates Bayes probabilities in various missing data scenarios (MCAR, MAR and MNAR). Empirically, we thoroughly compare various methods (constant and iterative imputations, complete case analysis, PbP, and an EM algorithm) across classification, probability estimation, calibration, and parameter inference. Our analysis provides a comprehensive view on the logistic regression with missing values. It reveals that mean imputation can be used as baseline for low sample sizes, and improved performance is obtained via nonlinear multiple iterative imputation techniques with the labels (MICE.RF.Y). For large sample sizes, PbP is the best method for Gaussian mixtures, and we recommend MICE.RF.Y in presence of nonlinear features.
Asymptotic Normality of Infinite Centered Random Forests -Application to Imbalanced Classification
Jun 10, 2025
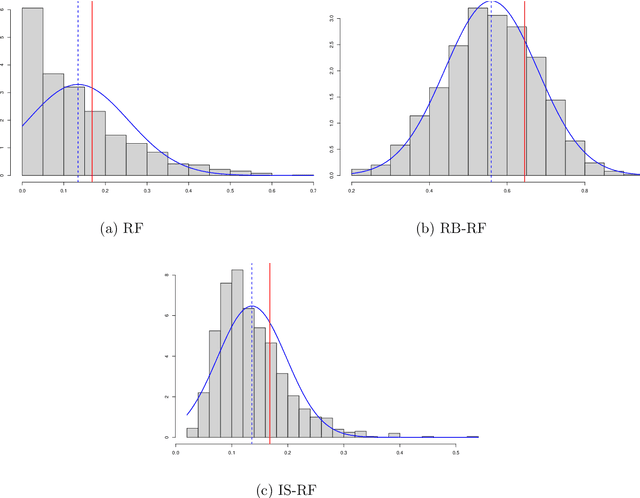
Abstract:Many classification tasks involve imbalanced data, in which a class is largely underrepresented. Several techniques consists in creating a rebalanced dataset on which a classifier is trained. In this paper, we study theoretically such a procedure, when the classifier is a Centered Random Forests (CRF). We establish a Central Limit Theorem (CLT) on the infinite CRF with explicit rates and exact constant. We then prove that the CRF trained on the rebalanced dataset exhibits a bias, which can be removed with appropriate techniques. Based on an importance sampling (IS) approach, the resulting debiased estimator, called IS-ICRF, satisfies a CLT centered at the prediction function value. For high imbalance settings, we prove that the IS-ICRF estimator enjoys a variance reduction compared to the ICRF trained on the original data. Therefore, our theoretical analysis highlights the benefits of training random forests on a rebalanced dataset (followed by a debiasing procedure) compared to using the original data. Our theoretical results, especially the variance rates and the variance reduction, appear to be valid for Breiman's random forests in our experiments.
Theoretical and experimental study of SMOTE: limitations and comparisons of rebalancing strategies
Feb 06, 2024Abstract:Synthetic Minority Oversampling Technique (SMOTE) is a common rebalancing strategy for handling imbalanced data sets. Asymptotically, we prove that SMOTE (with default parameter) regenerates the original distribution by simply copying the original minority samples. We also prove that SMOTE density vanishes near the boundary of the support of the minority distribution, therefore justifying the common BorderLine SMOTE strategy. Then we introduce two new SMOTE-related strategies, and compare them with state-of-the-art rebalancing procedures. We show that rebalancing strategies are only required when the data set is highly imbalanced. For such data sets, SMOTE, our proposals, or undersampling procedures are the best strategies.
Random features models: a way to study the success of naive imputation
Feb 06, 2024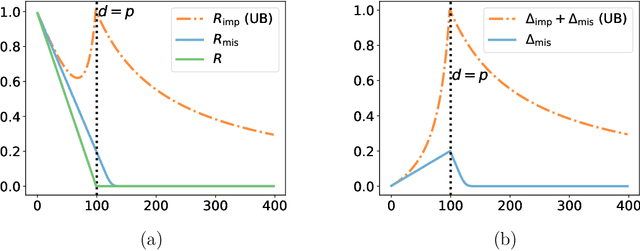

Abstract:Constant (naive) imputation is still widely used in practice as this is a first easy-to-use technique to deal with missing data. Yet, this simple method could be expected to induce a large bias for prediction purposes, as the imputed input may strongly differ from the true underlying data. However, recent works suggest that this bias is low in the context of high-dimensional linear predictors when data is supposed to be missing completely at random (MCAR). This paper completes the picture for linear predictors by confirming the intuition that the bias is negligible and that surprisingly naive imputation also remains relevant in very low dimension.To this aim, we consider a unique underlying random features model, which offers a rigorous framework for studying predictive performances, whilst the dimension of the observed features varies.Building on these theoretical results, we establish finite-sample bounds on stochastic gradient (SGD) predictors applied to zero-imputed data, a strategy particularly well suited for large-scale learning.If the MCAR assumption appears to be strong, we show that similar favorable behaviors occur for more complex missing data scenarios.
Sparse tree-based initialization for neural networks
Sep 30, 2022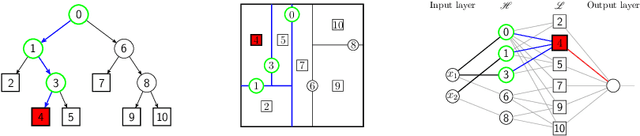
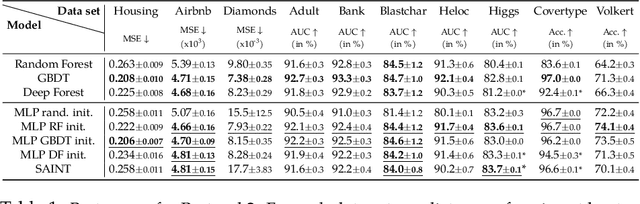
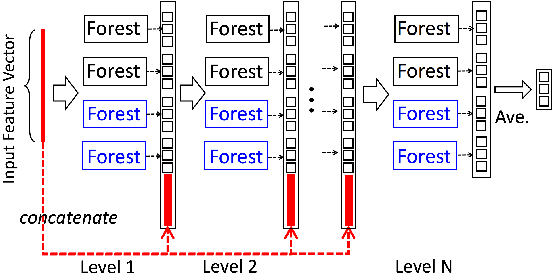
Abstract:Dedicated neural network (NN) architectures have been designed to handle specific data types (such as CNN for images or RNN for text), which ranks them among state-of-the-art methods for dealing with these data. Unfortunately, no architecture has been found for dealing with tabular data yet, for which tree ensemble methods (tree boosting, random forests) usually show the best predictive performances. In this work, we propose a new sparse initialization technique for (potentially deep) multilayer perceptrons (MLP): we first train a tree-based procedure to detect feature interactions and use the resulting information to initialize the network, which is subsequently trained via standard stochastic gradient strategies. Numerical experiments on several tabular data sets show that this new, simple and easy-to-use method is a solid concurrent, both in terms of generalization capacity and computation time, to default MLP initialization and even to existing complex deep learning solutions. In fact, this wise MLP initialization raises the resulting NN methods to the level of a valid competitor to gradient boosting when dealing with tabular data. Besides, such initializations are able to preserve the sparsity of weights introduced in the first layers of the network through training. This fact suggests that this new initializer operates an implicit regularization during the NN training, and emphasizes that the first layers act as a sparse feature extractor (as for convolutional layers in CNN).
Minimax rate of consistency for linear models with missing values
Feb 03, 2022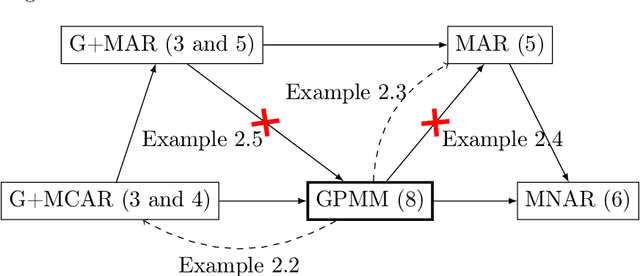

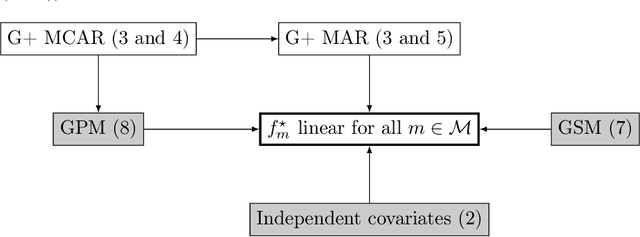
Abstract:Missing values arise in most real-world data sets due to the aggregation of multiple sources and intrinsically missing information (sensor failure, unanswered questions in surveys...). In fact, the very nature of missing values usually prevents us from running standard learning algorithms. In this paper, we focus on the extensively-studied linear models, but in presence of missing values, which turns out to be quite a challenging task. Indeed, the Bayes rule can be decomposed as a sum of predictors corresponding to each missing pattern. This eventually requires to solve a number of learning tasks, exponential in the number of input features, which makes predictions impossible for current real-world datasets. First, we propose a rigorous setting to analyze a least-square type estimator and establish a bound on the excess risk which increases exponentially in the dimension. Consequently, we leverage the missing data distribution to propose a new algorithm, andderive associated adaptive risk bounds that turn out to be minimax optimal. Numerical experiments highlight the benefits of our method compared to state-of-the-art algorithms used for predictions with missing values.
What's a good imputation to predict with missing values?
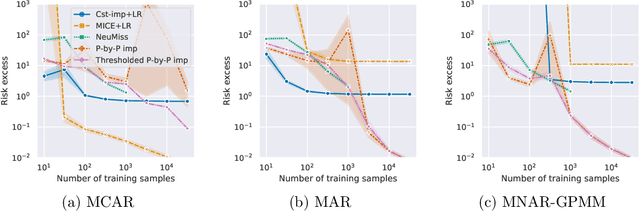
Jun 01, 2021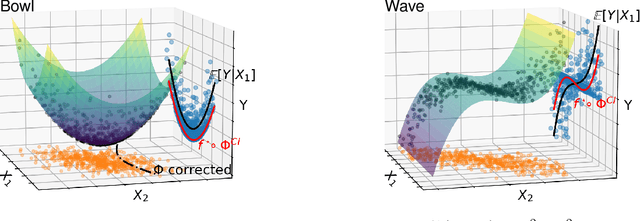
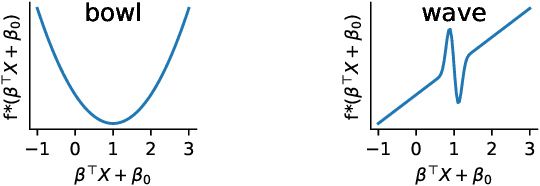
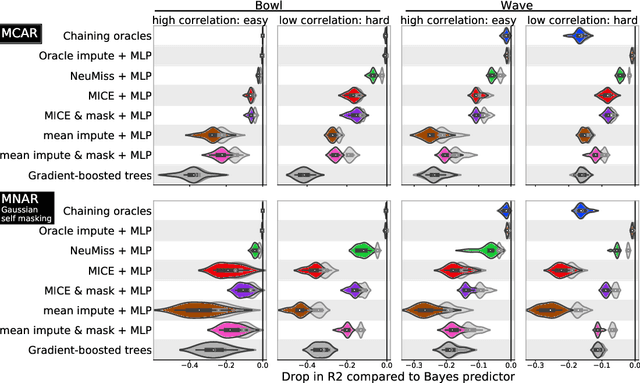
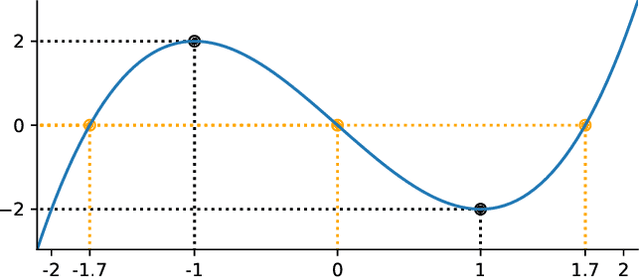
Abstract:How to learn a good predictor on data with missing values? Most efforts focus on first imputing as well as possible and second learning on the completed data to predict the outcome. Yet, this widespread practice has no theoretical grounding. Here we show that for almost all imputation functions, an impute-then-regress procedure with a powerful learner is Bayes optimal. This result holds for all missing-values mechanisms, in contrast with the classic statistical results that require missing-at-random settings to use imputation in probabilistic modeling. Moreover, it implies that perfect conditional imputation may not be needed for good prediction asymptotically. In fact, we show that on perfectly imputed data the best regression function will generally be discontinuous, which makes it hard to learn. Crafting instead the imputation so as to leave the regression function unchanged simply shifts the problem to learning discontinuous imputations. Rather, we suggest that it is easier to learn imputation and regression jointly. We propose such a procedure, adapting NeuMiss, a neural network capturing the conditional links across observed and unobserved variables whatever the missing-value pattern. Experiments confirm that joint imputation and regression through NeuMiss is better than various two step procedures in our experiments with finite number of samples.
SHAFF: Fast and consistent SHApley eFfect estimates via random Forests
May 25, 2021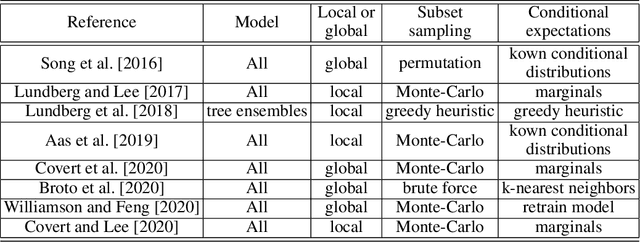
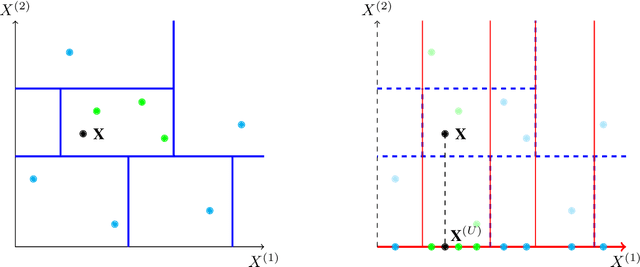
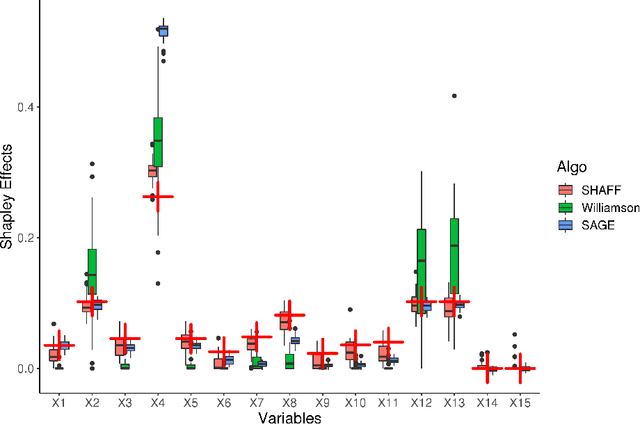
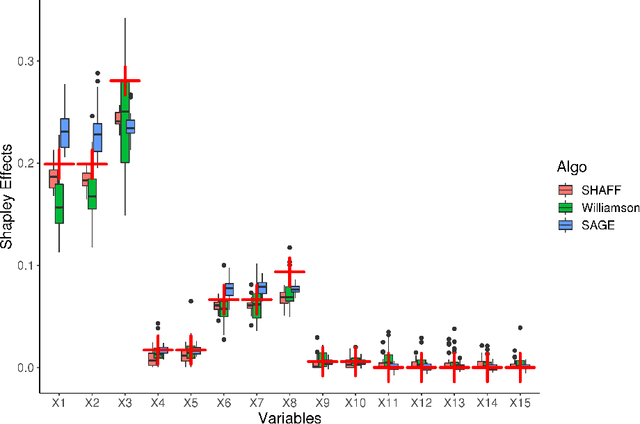
Abstract:Interpretability of learning algorithms is crucial for applications involving critical decisions, and variable importance is one of the main interpretation tools. Shapley effects are now widely used to interpret both tree ensembles and neural networks, as they can efficiently handle dependence and interactions in the data, as opposed to most other variable importance measures. However, estimating Shapley effects is a challenging task, because of the computational complexity and the conditional expectation estimates. Accordingly, existing Shapley algorithms have flaws: a costly running time, or a bias when input variables are dependent. Therefore, we introduce SHAFF, SHApley eFfects via random Forests, a fast and accurate Shapley effect estimate, even when input variables are dependent. We show SHAFF efficiency through both a theoretical analysis of its consistency, and the practical performance improvements over competitors with extensive experiments. An implementation of SHAFF in C++ and R is available online.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge