BYO-Eval: Build Your Own Dataset for Fine-Grained Visual Assessment of Multimodal Language Models

Visual Language Models (VLMs) are now sufficiently advanced to support a broad range of applications, including answering complex visual questions, and are increasingly expected to interact with images in varied ways. To evaluate them, current benchmarks often focus on specific domains (e.g., reading charts), constructing datasets of annotated real images paired with pre-defined Multiple Choice Questions (MCQs) to report aggregate accuracy scores. However, such benchmarks entail high annotation costs, risk information leakage, and do not clarify whether failures stem from limitations in visual perception, reasoning, or general knowledge. We propose a new evaluation methodology, inspired by ophthalmologic diagnostics, leveraging procedural generation of synthetic images to obtain control over visual attributes and precisely reveal perception failures in VLMs. Specifically, we build collections of images with gradually more challenging variations in the content of interest (e.g., number of objects in a counting task) while holding other visual parameters constant. This diagnostic allows systematic stress testing and fine-grained failure analysis, shifting the focus from coarse benchmarking toward targeted and interpretable assessment of VLM capabilities. Our code is available at https://github.com/byoeval/BYO-EVAL.

Sparse tree-based initialization for neural networks

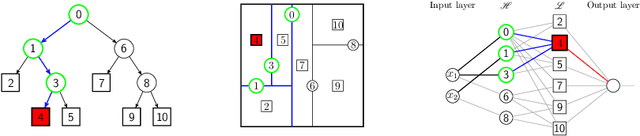
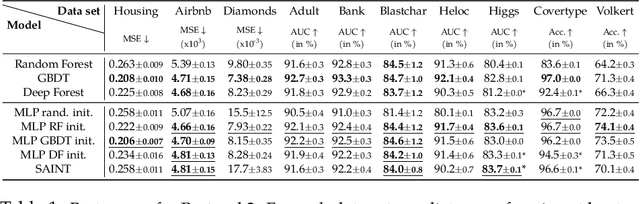
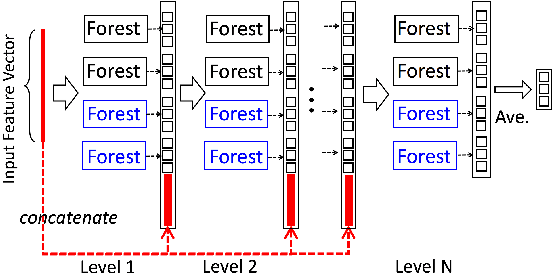
Dedicated neural network (NN) architectures have been designed to handle specific data types (such as CNN for images or RNN for text), which ranks them among state-of-the-art methods for dealing with these data. Unfortunately, no architecture has been found for dealing with tabular data yet, for which tree ensemble methods (tree boosting, random forests) usually show the best predictive performances. In this work, we propose a new sparse initialization technique for (potentially deep) multilayer perceptrons (MLP): we first train a tree-based procedure to detect feature interactions and use the resulting information to initialize the network, which is subsequently trained via standard stochastic gradient strategies. Numerical experiments on several tabular data sets show that this new, simple and easy-to-use method is a solid concurrent, both in terms of generalization capacity and computation time, to default MLP initialization and even to existing complex deep learning solutions. In fact, this wise MLP initialization raises the resulting NN methods to the level of a valid competitor to gradient boosting when dealing with tabular data. Besides, such initializations are able to preserve the sparsity of weights introduced in the first layers of the network through training. This fact suggests that this new initializer operates an implicit regularization during the NN training, and emphasizes that the first layers act as a sparse feature extractor (as for convolutional layers in CNN).

Analyzing the tree-layer structure of Deep Forests

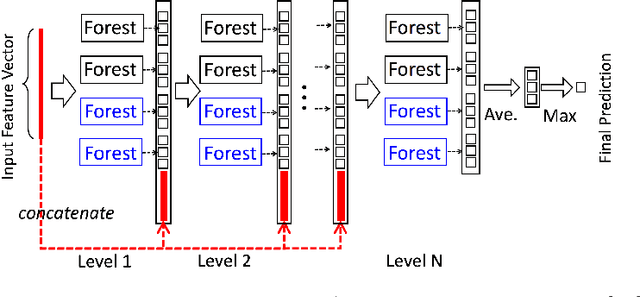
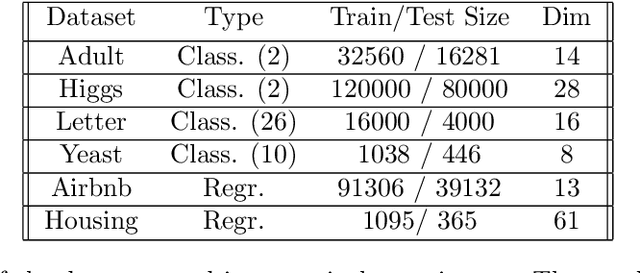
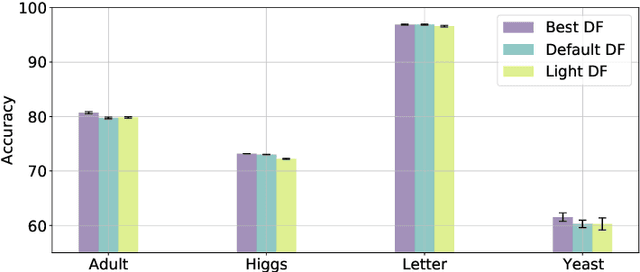
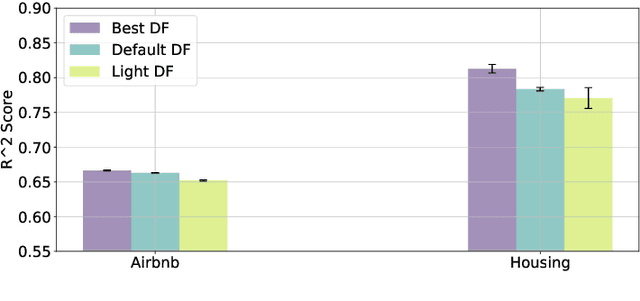
Random forests on the one hand, and neural networks on the other hand, have met great success in the machine learning community for their predictive performance. Combinations of both have been proposed in the literature, notably leading to the so-called deep forests (DF) [25]. In this paper, we investigate the mechanisms at work in DF and outline that DF architecture can generally be simplified into more simple and computationally efficient shallow forests networks. Despite some instability, the latter may outperform standard predictive tree-based methods. In order to precisely quantify the improvement achieved by these light network configurations over standard tree learners, we theoretically study the performance of a shallow tree network made of two layers, each one composed of a single centered tree. We provide tight theoretical lower and upper bounds on its excess risk. These theoretical results show the interest of tree-network architectures for well-structured data provided that the first layer, acting as a data encoder, is rich enough.