Random features models: a way to study the success of naive imputation

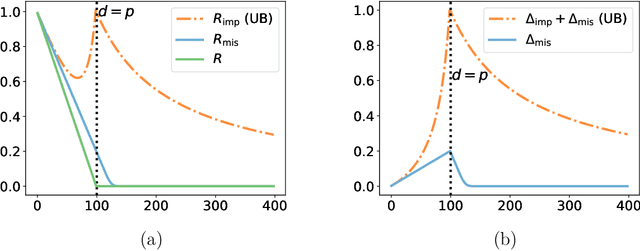
Constant (naive) imputation is still widely used in practice as this is a first easy-to-use technique to deal with missing data. Yet, this simple method could be expected to induce a large bias for prediction purposes, as the imputed input may strongly differ from the true underlying data. However, recent works suggest that this bias is low in the context of high-dimensional linear predictors when data is supposed to be missing completely at random (MCAR). This paper completes the picture for linear predictors by confirming the intuition that the bias is negligible and that surprisingly naive imputation also remains relevant in very low dimension.To this aim, we consider a unique underlying random features model, which offers a rigorous framework for studying predictive performances, whilst the dimension of the observed features varies.Building on these theoretical results, we establish finite-sample bounds on stochastic gradient (SGD) predictors applied to zero-imputed data, a strategy particularly well suited for large-scale learning.If the MCAR assumption appears to be strong, we show that similar favorable behaviors occur for more complex missing data scenarios.

Minimax rate of consistency for linear models with missing values

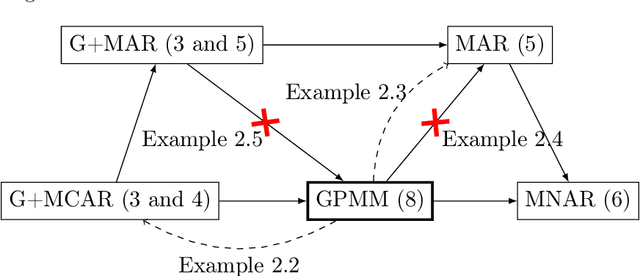
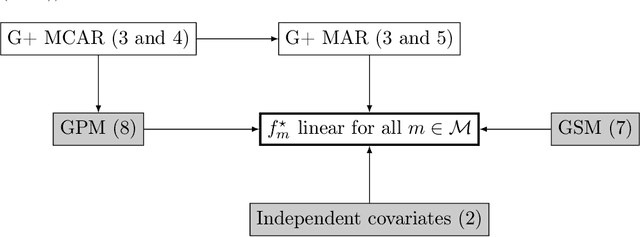
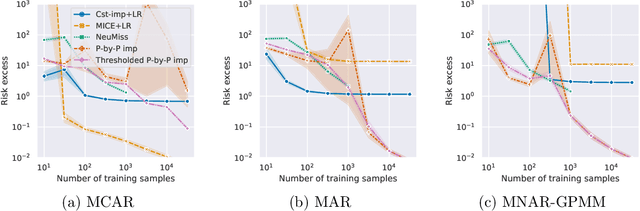
Missing values arise in most real-world data sets due to the aggregation of multiple sources and intrinsically missing information (sensor failure, unanswered questions in surveys...). In fact, the very nature of missing values usually prevents us from running standard learning algorithms. In this paper, we focus on the extensively-studied linear models, but in presence of missing values, which turns out to be quite a challenging task. Indeed, the Bayes rule can be decomposed as a sum of predictors corresponding to each missing pattern. This eventually requires to solve a number of learning tasks, exponential in the number of input features, which makes predictions impossible for current real-world datasets. First, we propose a rigorous setting to analyze a least-square type estimator and establish a bound on the excess risk which increases exponentially in the dimension. Consequently, we leverage the missing data distribution to propose a new algorithm, andderive associated adaptive risk bounds that turn out to be minimax optimal. Numerical experiments highlight the benefits of our method compared to state-of-the-art algorithms used for predictions with missing values.