Imputation for prediction: beware of diminishing returns

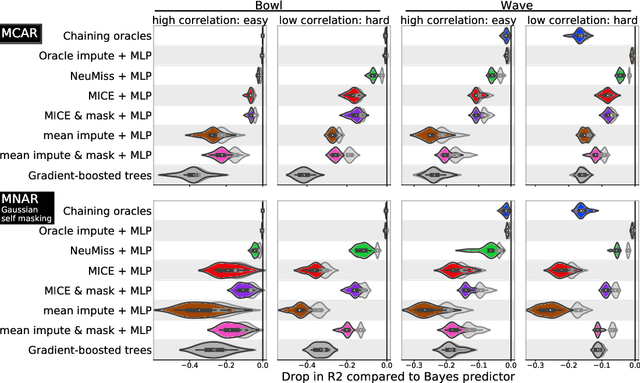
Missing values are prevalent across various fields, posing challenges for training and deploying predictive models. In this context, imputation is a common practice, driven by the hope that accurate imputations will enhance predictions. However, recent theoretical and empirical studies indicate that simple constant imputation can be consistent and competitive. This empirical study aims at clarifying if and when investing in advanced imputation methods yields significantly better predictions. Relating imputation and predictive accuracies across combinations of imputation and predictive models on 20 datasets, we show that imputation accuracy matters less i) when using expressive models, ii) when incorporating missingness indicators as complementary inputs, iii) matters much more for generated linear outcomes than for real-data outcomes. Interestingly, we also show that the use of the missingness indicator is beneficial to the prediction performance, even in MCAR scenarios. Overall, on real-data with powerful models, improving imputation only has a minor effect on prediction performance. Thus, investing in better imputations for improved predictions often offers limited benefits.

Beyond calibration: estimating the grouping loss of modern neural networks

Good decision making requires machine-learning models to provide trustworthy confidence scores. To this end, recent work has focused on miscalibration, i.e, the over or under confidence of model scores. Yet, contrary to widespread belief, calibration is not enough: even a classifier with the best possible accuracy and perfect calibration can have confidence scores far from the true posterior probabilities. This is due to the grouping loss, created by samples with the same confidence scores but different true posterior probabilities. Proper scoring rule theory shows that given the calibration loss, the missing piece to characterize individual errors is the grouping loss. While there are many estimators of the calibration loss, none exists for the grouping loss in standard settings. Here, we propose an estimator to approximate the grouping loss. We use it to study modern neural network architectures in vision and NLP. We find that the grouping loss varies markedly across architectures, and that it is a key model-comparison factor across the most accurate, calibrated, models. We also show that distribution shifts lead to high grouping loss.

Benchmarking missing-values approaches for predictive models on health databases

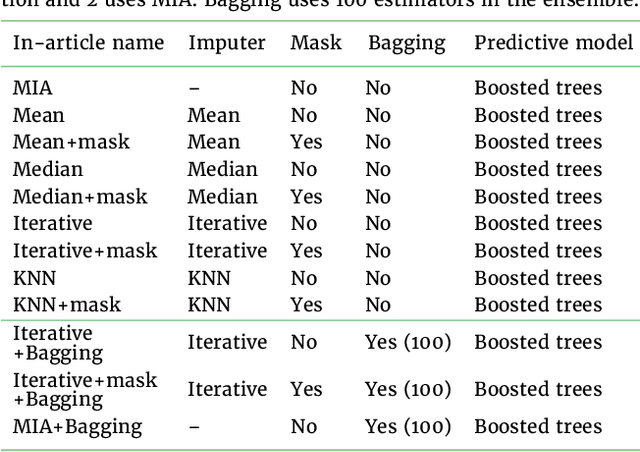
BACKGROUND: As databases grow larger, it becomes harder to fully control their collection, and they frequently come with missing values: incomplete observations. These large databases are well suited to train machine-learning models, for instance for forecasting or to extract biomarkers in biomedical settings. Such predictive approaches can use discriminative -- rather than generative -- modeling, and thus open the door to new missing-values strategies. Yet existing empirical evaluations of strategies to handle missing values have focused on inferential statistics. RESULTS: Here we conduct a systematic benchmark of missing-values strategies in predictive models with a focus on large health databases: four electronic health record datasets, a population brain imaging one, a health survey and two intensive care ones. Using gradient-boosted trees, we compare native support for missing values with simple and state-of-the-art imputation prior to learning. We investigate prediction accuracy and computational time. For prediction after imputation, we find that adding an indicator to express which values have been imputed is important, suggesting that the data are missing not at random. Elaborate missing values imputation can improve prediction compared to simple strategies but requires longer computational time on large data. Learning trees that model missing values-with missing incorporated attribute-leads to robust, fast, and well-performing predictive modeling. CONCLUSIONS: Native support for missing values in supervised machine learning predicts better than state-of-the-art imputation with much less computational cost. When using imputation, it is important to add indicator columns expressing which values have been imputed.

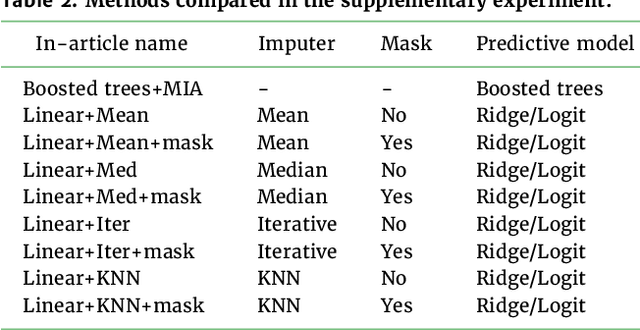
What's a good imputation to predict with missing values?

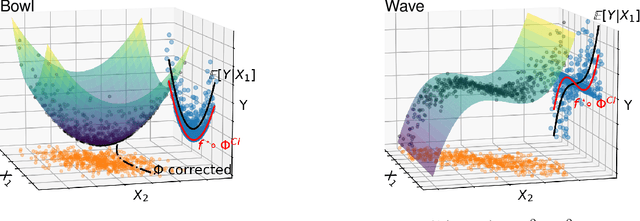
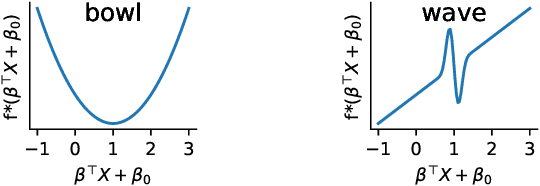
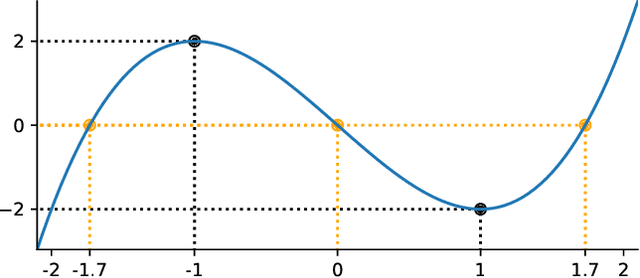
How to learn a good predictor on data with missing values? Most efforts focus on first imputing as well as possible and second learning on the completed data to predict the outcome. Yet, this widespread practice has no theoretical grounding. Here we show that for almost all imputation functions, an impute-then-regress procedure with a powerful learner is Bayes optimal. This result holds for all missing-values mechanisms, in contrast with the classic statistical results that require missing-at-random settings to use imputation in probabilistic modeling. Moreover, it implies that perfect conditional imputation may not be needed for good prediction asymptotically. In fact, we show that on perfectly imputed data the best regression function will generally be discontinuous, which makes it hard to learn. Crafting instead the imputation so as to leave the regression function unchanged simply shifts the problem to learning discontinuous imputations. Rather, we suggest that it is easier to learn imputation and regression jointly. We propose such a procedure, adapting NeuMiss, a neural network capturing the conditional links across observed and unobserved variables whatever the missing-value pattern. Experiments confirm that joint imputation and regression through NeuMiss is better than various two step procedures in our experiments with finite number of samples.

Neumann networks: differential programming for supervised learning with missing values

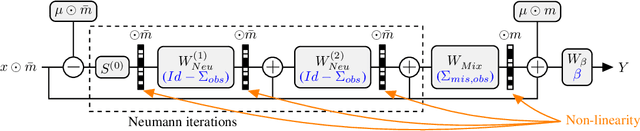
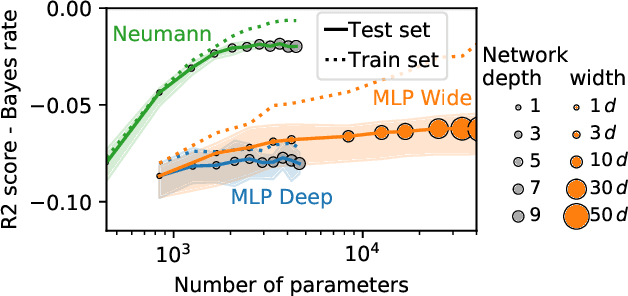
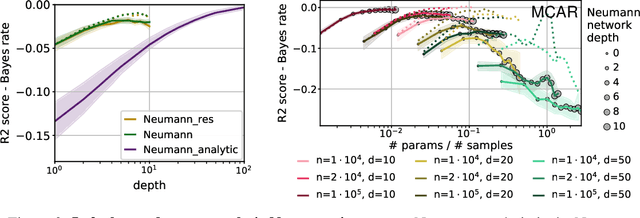
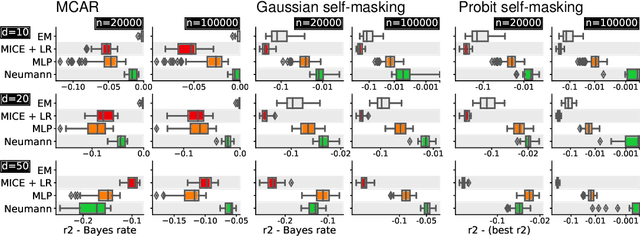
The presence of missing values makes supervised learning much more challenging. Indeed, previous work has shown that even when the response is a linear function of the complete data, the optimal predictor is a complex function of the observed entries and the missingness indicator. As a result, the computational or sample complexities of consistent approaches depend on the number of missing patterns, which can be exponential in the number of dimensions. In this work, we derive the analytical form of the optimal predictor under a linearity assumption and various missing data mechanisms including Missing at Random (MAR) and self-masking (Missing Not At Random). Based on a Neumann series approximation of the optimal predictor, we propose a new principled architecture, named Neumann networks. Their originality and strength comes from the use of a new type of non-linearity: the multiplication by the missingness indicator. We provide an upper bound on the Bayes risk of Neumann networks, and show that they have good predictive accuracy with both a number of parameters and a computational complexity independent of the number of missing data patterns. As a result they scale well to problems with many features, and remain statistically efficient for medium-sized samples. Moreover, we show that, contrary to procedures using EM or imputation, they are robust to the missing data mechanism, including difficult MNAR settings such as self-masking.

Linear predictor on linearly-generated data with missing values: non consistency and solutions

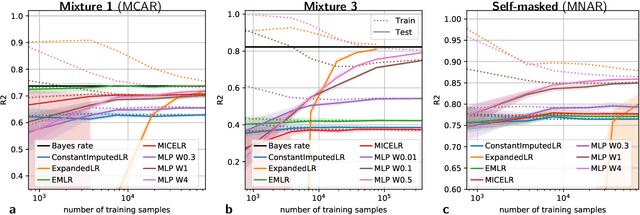
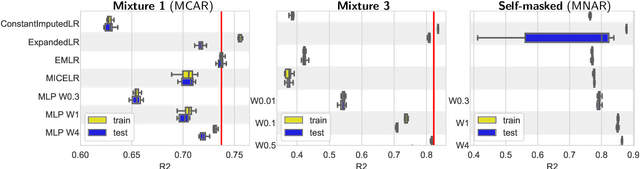
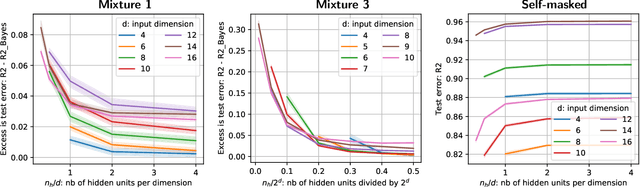
We consider building predictors when the data have missing values. We study the seemingly-simple case where the target to predict is a linear function of the fully-observed data and we show that, in the presence of missing values, the optimal predictor may not be linear. In the particular Gaussian case, it can be written as a linear function of multiway interactions between the observed data and the various missing-value indicators. Due to its intrinsic complexity, we study a simple approximation and prove generalization bounds with finite samples, highlighting regimes for which each method performs best. We then show that multilayer perceptrons with ReLU activation functions can be consistent, and can explore good trade-offs between the true model and approximations. Our study highlights the interesting family of models that are beneficial to fit with missing values depending on the amount of data available.

WHInter: A Working set algorithm for High-dimensional sparse second order Interaction models

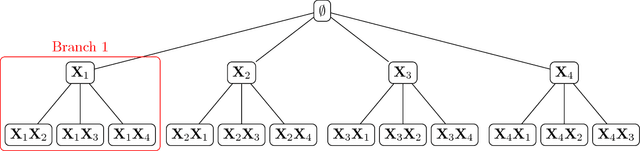
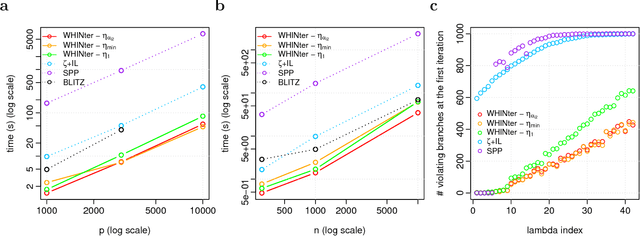
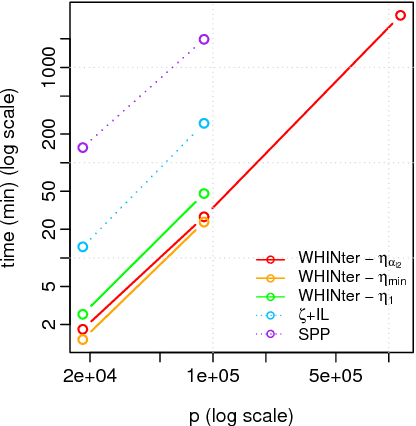
Learning sparse linear models with two-way interactions is desirable in many application domains such as genomics. l1-regularised linear models are popular to estimate sparse models, yet standard implementations fail to address specifically the quadratic explosion of candidate two-way interactions in high dimensions, and typically do not scale to genetic data with hundreds of thousands of features. Here we present WHInter, a working set algorithm to solve large l1-regularised problems with two-way interactions for binary design matrices. The novelty of WHInter stems from a new bound to efficiently identify working sets while avoiding to scan all features, and on fast computations inspired from solutions to the maximum inner product search problem. We apply WHInter to simulated and real genetic data and show that it is more scalable and two orders of magnitude faster than the state of the art.

Supervised Quantile Normalisation

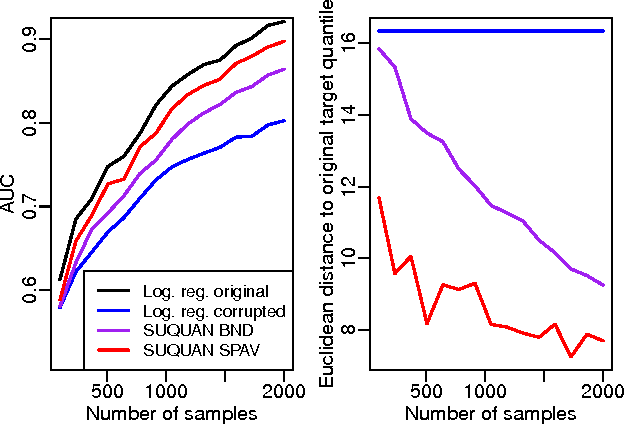
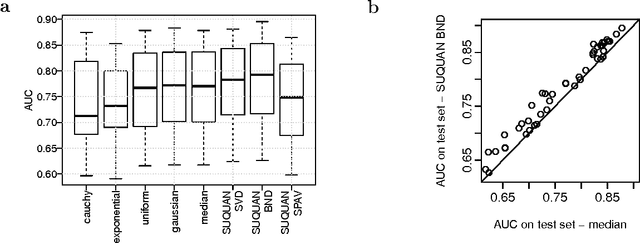
Quantile normalisation is a popular normalisation method for data subject to unwanted variations such as images, speech, or genomic data. It applies a monotonic transformation to the feature values of each sample to ensure that after normalisation, they follow the same target distribution for each sample. Choosing a "good" target distribution remains however largely empirical and heuristic, and is usually done independently of the subsequent analysis of normalised data. We propose instead to couple the quantile normalisation step with the subsequent analysis, and to optimise the target distribution jointly with the other parameters in the analysis. We illustrate this principle on the problem of estimating a linear model over normalised data, and show that it leads to a particular low-rank matrix regression problem that can be solved efficiently. We illustrate the potential of our method, which we term SUQUAN, on simulated data, images and genomic data, where it outperforms standard quantile normalisation.