Linear predictor on linearly-generated data with missing values: non consistency and solutions

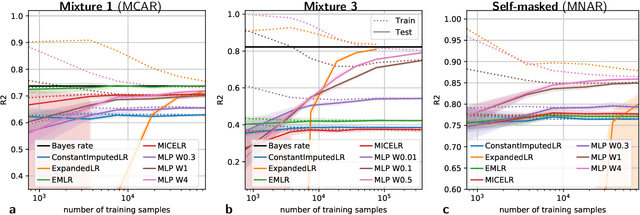
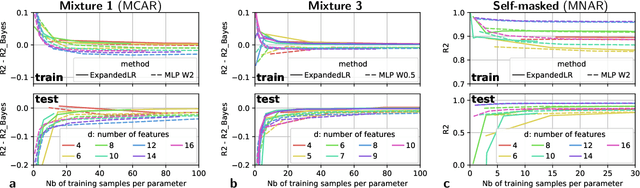
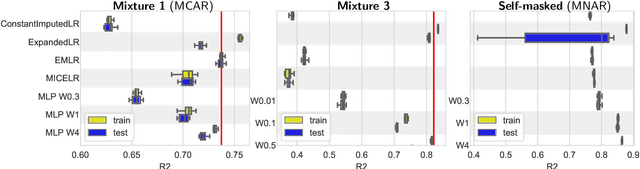
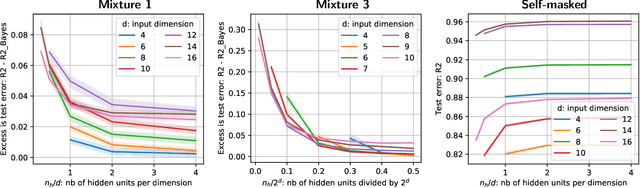
We consider building predictors when the data have missing values. We study the seemingly-simple case where the target to predict is a linear function of the fully-observed data and we show that, in the presence of missing values, the optimal predictor may not be linear. In the particular Gaussian case, it can be written as a linear function of multiway interactions between the observed data and the various missing-value indicators. Due to its intrinsic complexity, we study a simple approximation and prove generalization bounds with finite samples, highlighting regimes for which each method performs best. We then show that multilayer perceptrons with ReLU activation functions can be consistent, and can explore good trade-offs between the true model and approximations. Our study highlights the interesting family of models that are beneficial to fit with missing values depending on the amount of data available.

On the consistency of supervised learning with missing values

In many application settings, the data have missing features which make data analysis challenging. An abundant literature addresses missing data in an inferential framework: estimating parameters and their variance from incomplete tables. Here, we consider supervised-learning settings: predicting a target when missing values appear in both training and testing data. We show the consistency of two approaches in prediction. A striking result is that the widely-used method of imputing with the mean prior to learning is consistent when missing values are not informative. This contrasts with inferential settings where mean imputation is pointed at for distorting the distribution of the data. That such a simple approach can be consistent is important in practice. We also show that a predictor suited for complete observations can predict optimally on incomplete data, through multiple imputation.We analyze further decision trees. These can naturally tackle empirical risk minimization with missing values, due to their ability to handle the half-discrete nature of incomplete variables. After comparing theoretically and empirically different missing values strategies in trees, we recommend using the ``missing incorporated in attribute'' method as it can handle both non-informative and informative missing values.