MMD-based Variable Importance for Distributional Random Forest

Distributional Random Forest (DRF) is a flexible forest-based method to estimate the full conditional distribution of a multivariate output of interest given input variables. In this article, we introduce a variable importance algorithm for DRFs, based on the well-established drop and relearn principle and MMD distance. While traditional importance measures only detect variables with an influence on the output mean, our algorithm detects variables impacting the output distribution more generally. We show that the introduced importance measure is consistent, exhibits high empirical performance on both real and simulated data, and outperforms competitors. In particular, our algorithm is highly efficient to select variables through recursive feature elimination, and can therefore provide small sets of variables to build accurate estimates of conditional output distributions.

Variable importance for causal forests: breaking down the heterogeneity of treatment effects

Causal random forests provide efficient estimates of heterogeneous treatment effects. However, forest algorithms are also well-known for their black-box nature, and therefore, do not characterize how input variables are involved in treatment effect heterogeneity, which is a strong practical limitation. In this article, we develop a new importance variable algorithm for causal forests, to quantify the impact of each input on the heterogeneity of treatment effects. The proposed approach is inspired from the drop and relearn principle, widely used for regression problems. Importantly, we show how to handle the forest retrain without a confounding variable. If the confounder is not involved in the treatment effect heterogeneity, the local centering step enforces consistency of the importance measure. Otherwise, when a confounder also impacts heterogeneity, we introduce a corrective term in the retrained causal forest to recover consistency. Additionally, experiments on simulated, semi-synthetic, and real data show the good performance of our importance measure, which outperforms competitors on several test cases. Experiments also show that our approach can be efficiently extended to groups of variables, providing key insights in practice.

Kernel Stein Discrepancy thinning: a theoretical perspective of pathologies and a practical fix with regularization

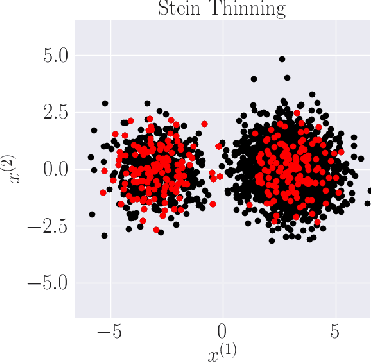
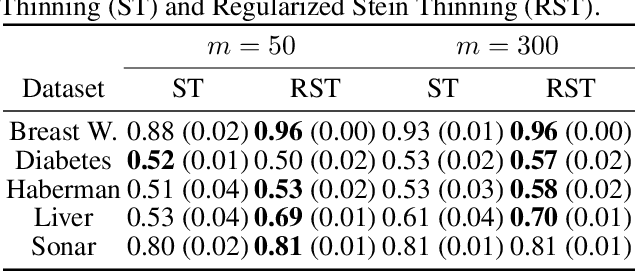
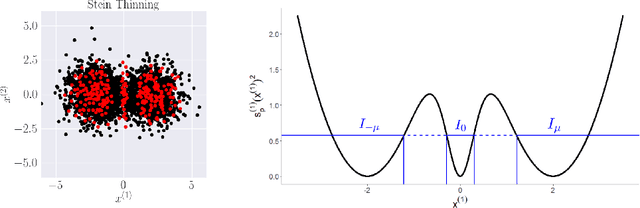
Stein thinning is a promising algorithm proposed by (Riabiz et al., 2022) for post-processing outputs of Markov chain Monte Carlo (MCMC). The main principle is to greedily minimize the kernelized Stein discrepancy (KSD), which only requires the gradient of the log-target distribution, and is thus well-suited for Bayesian inference. The main advantages of Stein thinning are the automatic remove of the burn-in period, the correction of the bias introduced by recent MCMC algorithms, and the asymptotic properties of convergence towards the target distribution. Nevertheless, Stein thinning suffers from several empirical pathologies, which may result in poor approximations, as observed in the literature. In this article, we conduct a theoretical analysis of these pathologies, to clearly identify the mechanisms at stake, and suggest improved strategies. Then, we introduce the regularized Stein thinning algorithm to alleviate the identified pathologies. Finally, theoretical guarantees and extensive experiments show the high efficiency of the proposed algorithm.

SHAFF: Fast and consistent SHApley eFfect estimates via random Forests

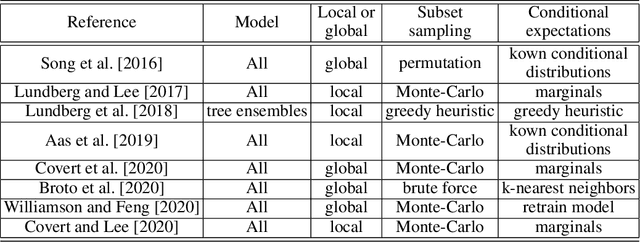
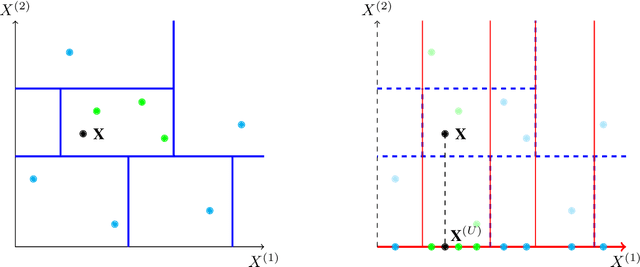
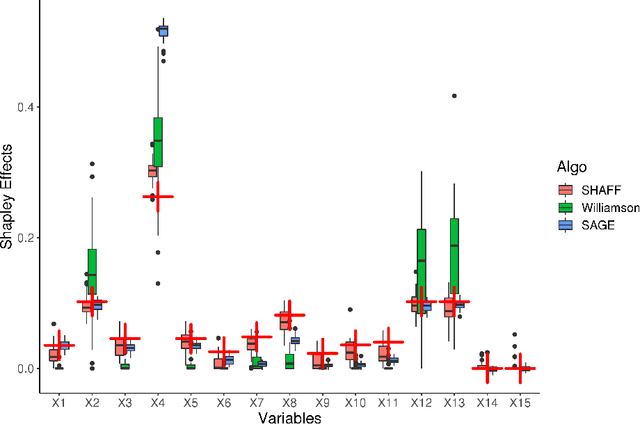
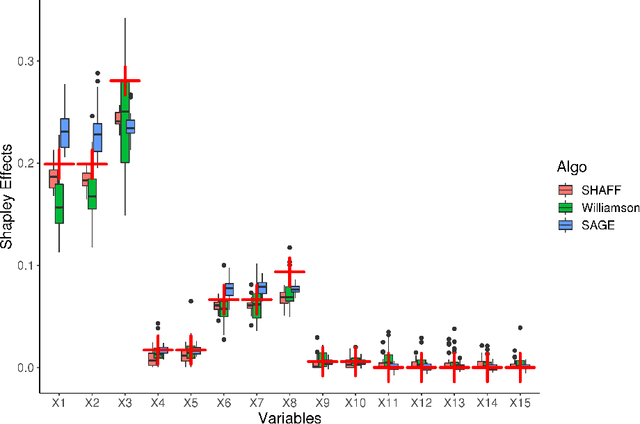
Interpretability of learning algorithms is crucial for applications involving critical decisions, and variable importance is one of the main interpretation tools. Shapley effects are now widely used to interpret both tree ensembles and neural networks, as they can efficiently handle dependence and interactions in the data, as opposed to most other variable importance measures. However, estimating Shapley effects is a challenging task, because of the computational complexity and the conditional expectation estimates. Accordingly, existing Shapley algorithms have flaws: a costly running time, or a bias when input variables are dependent. Therefore, we introduce SHAFF, SHApley eFfects via random Forests, a fast and accurate Shapley effect estimate, even when input variables are dependent. We show SHAFF efficiency through both a theoretical analysis of its consistency, and the practical performance improvements over competitors with extensive experiments. An implementation of SHAFF in C++ and R is available online.

MDA for random forests: inconsistency, and a practical solution via the Sobol-MDA

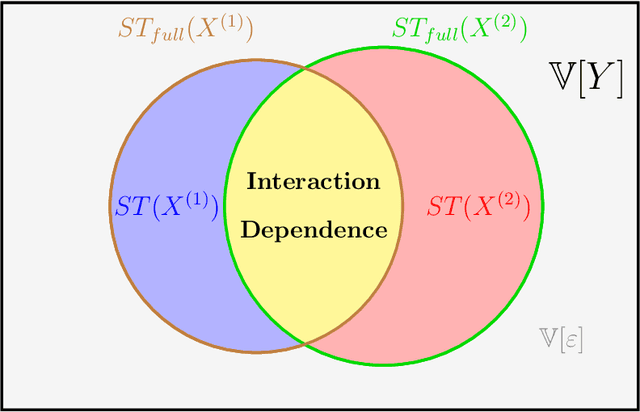
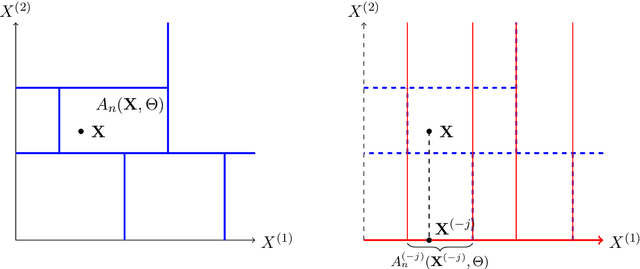
Variable importance measures are the main tools to analyze the black-box mechanism of random forests. Although the Mean Decrease Accuracy (MDA) is widely accepted as the most efficient variable importance measure for random forests, little is known about its theoretical properties. In fact, the exact MDA definition varies across the main random forest software. In this article, our objective is to rigorously analyze the behavior of the main MDA implementations. Consequently, we mathematically formalize the various implemented MDA algorithms, and then establish their limits when the sample size increases. In particular, we break down these limits in three components: the first two are related to Sobol indices, which are well-defined measures of a variable contribution to the output variance, widely used in the sensitivity analysis field, as opposed to the third term, whose value increases with dependence within input variables. Thus, we theoretically demonstrate that the MDA does not target the right quantity when inputs are dependent, a fact that has already been noticed experimentally. To address this issue, we define a new importance measure for random forests, the Sobol-MDA, which fixes the flaws of the original MDA. We prove the consistency of the Sobol-MDA and show its good empirical performance through experiments on both simulated and real data. An open source implementation in R and C++ is available online.

Interpretable Random Forests via Rule Extraction

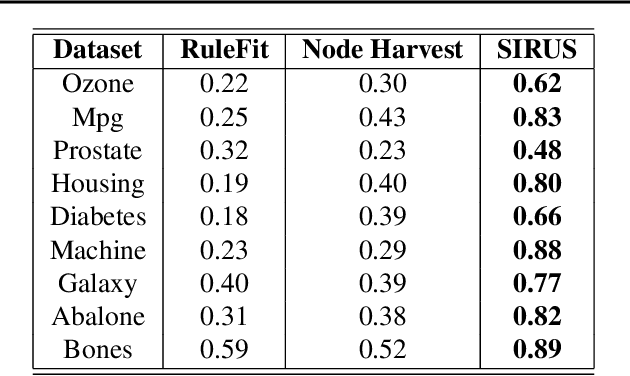
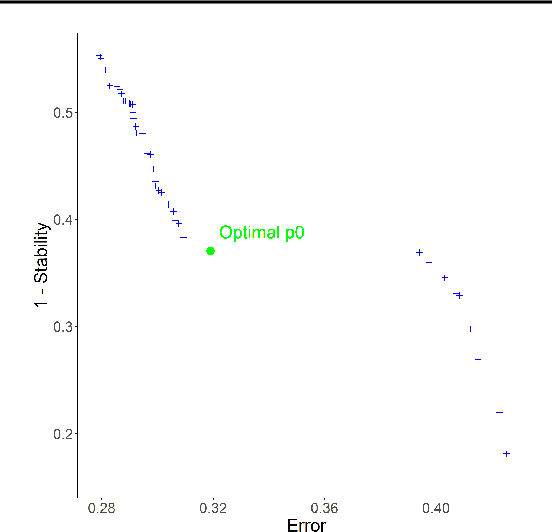
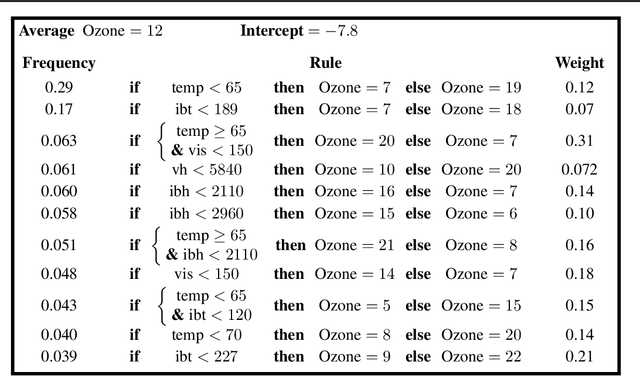
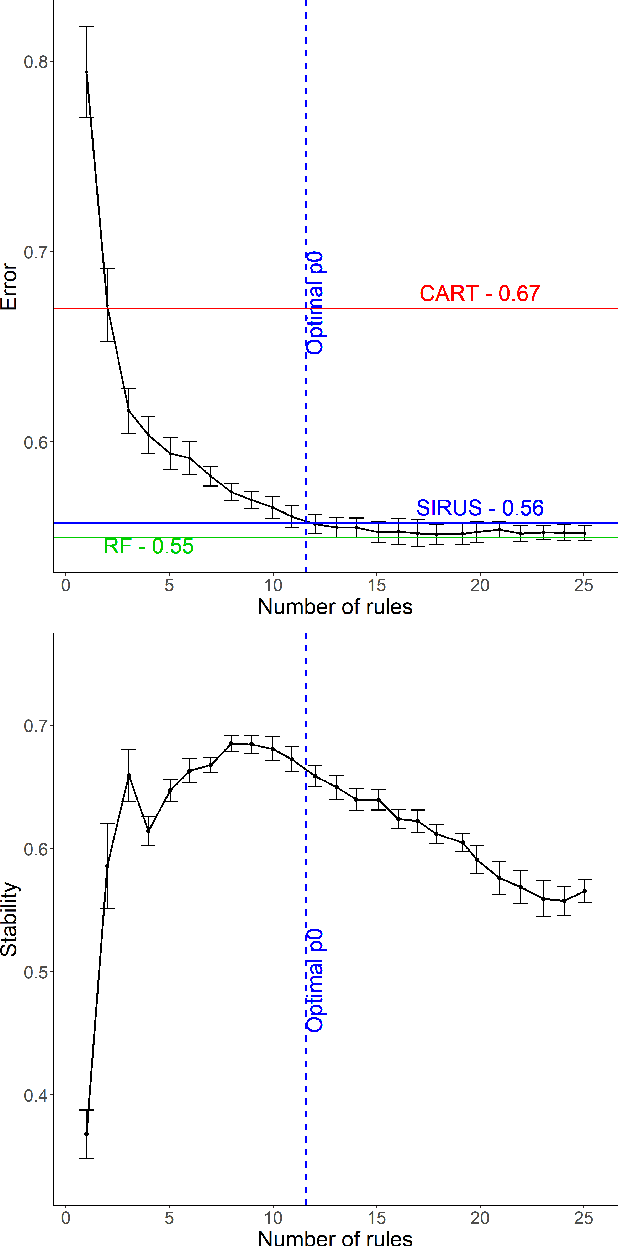
We introduce SIRUS (Stable and Interpretable RUle Set) for regression, a stable rule learning algorithm which takes the form of a short and simple list of rules. State-of-the-art learning algorithms are often referred to as "black boxes" because of the high number of operations involved in their prediction process. Despite their powerful predictivity, this lack of interpretability may be highly restrictive for applications with critical decisions at stake. On the other hand, algorithms with a simple structure-typically decision trees, rule algorithms, or sparse linear models-are well known for their instability. This undesirable feature makes the conclusions of the data analysis unreliable and turns out to be a strong operational limitation. This motivates the design of SIRUS, which combines a simple structure with a remarkable stable behavior when data is perturbed. The algorithm is based on random forests, the predictive accuracy of which is preserved. We demonstrate the efficiency of the method both empirically (through experiments) and theoretically (with the proof of its asymptotic stability). Our R/C++ software implementation sirus is available from CRAN.

SIRUS: Making Random Forests Interpretable

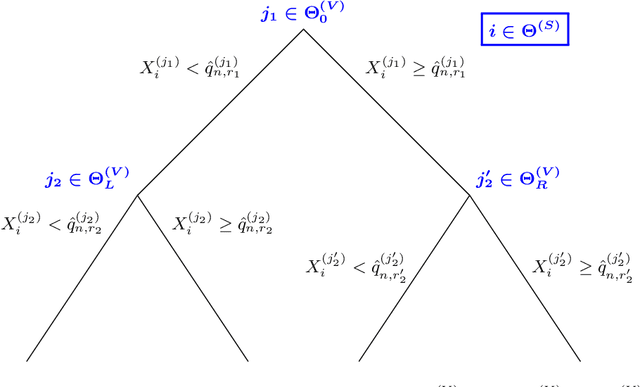
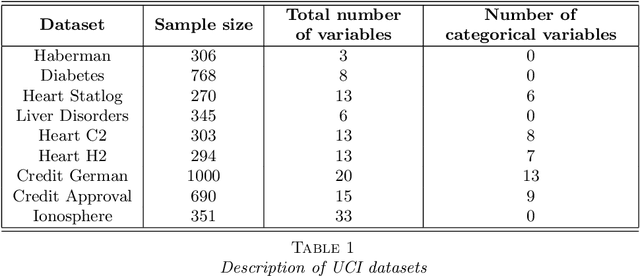
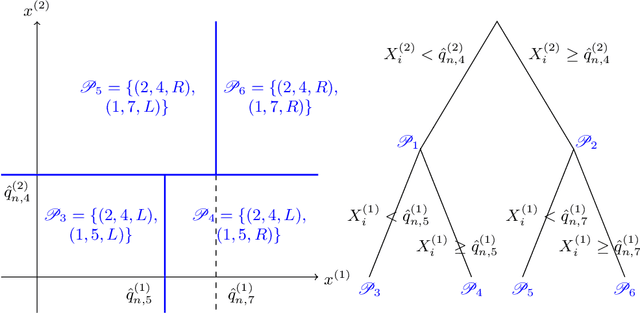
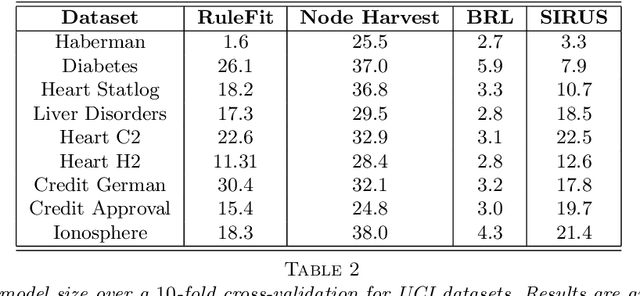
State-of-the-art learning algorithms, such as random forests or neural networks, are often qualified as ''black-boxes'' because of the high number and complexity of operations involved in their prediction mechanism. This lack of interpretability is a strong limitation for applications involving critical decisions, typically the analysis of production processes in the manufacturing industry. In such critical contexts, models have to be interpretable, i.e., simple, stable, and predictive. To address this issue, we design SIRUS (Stable and Interpretable RUle Set), a new classification algorithm based on random forests, which takes the form of a short list of rules. While simple models are usually unstable with respect to data perturbation, SIRUS achieves a remarkable stability improvement over cutting-edge methods. Furthermore, SIRUS inherits a predictive accuracy close to random forests, combined with the simplicity of decision trees. These properties are assessed both from a theoretical and empirical point of view, through extensive numerical experiments based on our R/C++ software implementation sirus available from CRAN.