Multivariate Online Linear Regression for Hierarchical Forecasting

In this paper, we consider a deterministic online linear regression model where we allow the responses to be multivariate. To address this problem, we introduce MultiVAW, a method that extends the well-known Vovk-Azoury-Warmuth algorithm to the multivariate setting, and show that it also enjoys logarithmic regret in time. We apply our results to the online hierarchical forecasting problem and recover an algorithm from this literature as a special case, allowing us to relax the hypotheses usually made for its analysis.

Online Inventory Problems: Beyond the i.i.d. Setting with Online Convex Optimization

We study multi-product inventory control problems where a manager makes sequential replenishment decisions based on partial historical information in order to minimize its cumulative losses. Our motivation is to consider general demands, losses and dynamics to go beyond standard models which usually rely on newsvendor-type losses, fixed dynamics, and unrealistic i.i.d. demand assumptions. We propose MaxCOSD, an online algorithm that has provable guarantees even for problems with non-i.i.d. demands and stateful dynamics, including for instance perishability. We consider what we call non-degeneracy assumptions on the demand process, and argue that they are necessary to allow learning.

Comparison of methods for early-readmission prediction in a high-dimensional heterogeneous covariates and time-to-event outcome framework

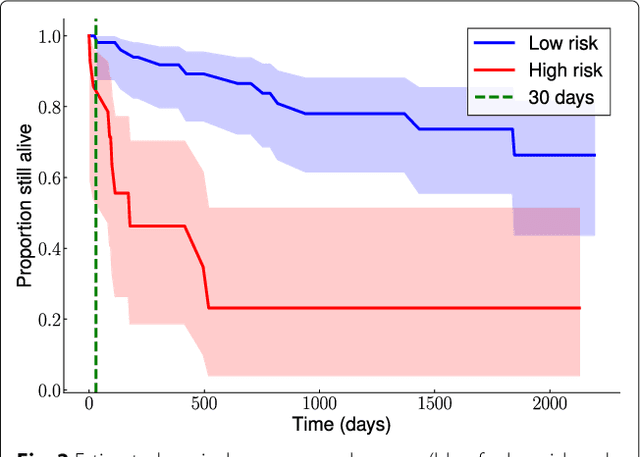
Background: Choosing the most performing method in terms of outcome prediction or variables selection is a recurring problem in prognosis studies, leading to many publications on methods comparison. But some aspects have received little attention. First, most comparison studies treat prediction performance and variable selection aspects separately. Second, methods are either compared within a binary outcome setting (based on an arbitrarily chosen delay) or within a survival setting, but not both. In this paper, we propose a comparison methodology to weight up those different settings both in terms of prediction and variables selection, while incorporating advanced machine learning strategies. Methods: Using a high-dimensional case study on a sickle-cell disease (SCD) cohort, we compare 8 statistical methods. In the binary outcome setting, we consider logistic regression (LR), support vector machine (SVM), random forest (RF), gradient boosting (GB) and neural network (NN); while on the survival analysis setting, we consider the Cox Proportional Hazards (PH), the CURE and the C-mix models. We then compare performances of all methods both in terms of risk prediction and variable selection, with a focus on the use of Elastic-Net regularization technique. Results: Among all assessed statistical methods assessed, the C-mix model yields the better performances in both the two considered settings, as well as interesting interpretation aspects. There is some consistency in selected covariates across methods within a setting, but not much across the two settings. Conclusions: It appears that learning withing the survival setting first, and then going back to a binary prediction using the survival estimates significantly enhance binary predictions.

Binacox: automatic cut-points detection in high-dimensional Cox model, with applications to genetic data

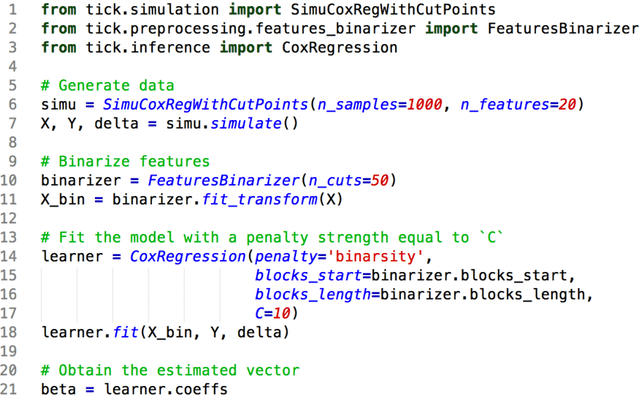
Determining significant prognostic biomarkers is of increasing importance in many areas of medicine. In order to translate a continuous biomarker into a clinical decision, it is often necessary to determine cut-points. There is so far no standard method to help evaluate how many cut-points are optimal for a given feature in a survival analysis setting. Moreover, most existing methods are univariate, hence not well suited for high-dimensional frameworks. This paper introduces a prognostic method called Binacox to deal with the problem of detecting multiple cut-points per features in a multivariate setting where a large number of continuous features are available. It is based on the Cox model and combines one-hot encodings with the binarsity penalty. This penalty uses total-variation regularization together with an extra linear constraint to avoid collinearity between the one-hot encodings and enable feature selection. A non-asymptotic oracle inequality is established. The statistical performance of the method is then examined on an extensive Monte Carlo simulation study, and finally illustrated on three publicly available genetic cancer datasets with high-dimensional features. On this datasets, our proposed methodology significantly outperforms the state-of-the-art survival models regarding risk prediction in terms of C-index, with a computing time orders of magnitude faster. In addition, it provides powerful interpretability by automatically pinpointing significant cut-points on relevant features from a clinical point of view.

C-mix: a high dimensional mixture model for censored durations, with applications to genetic data

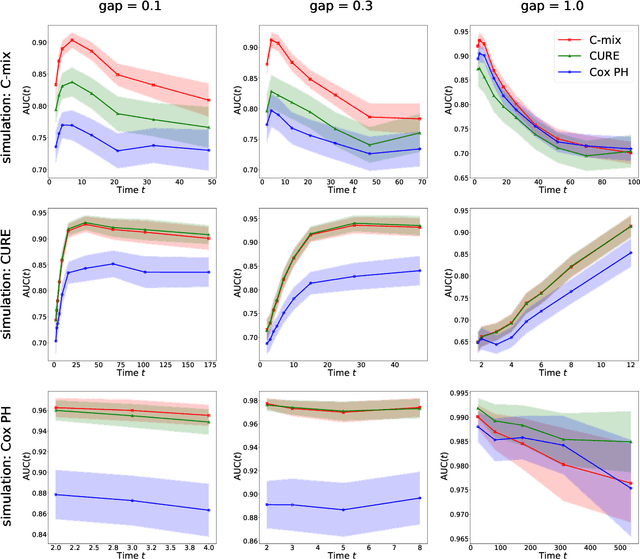
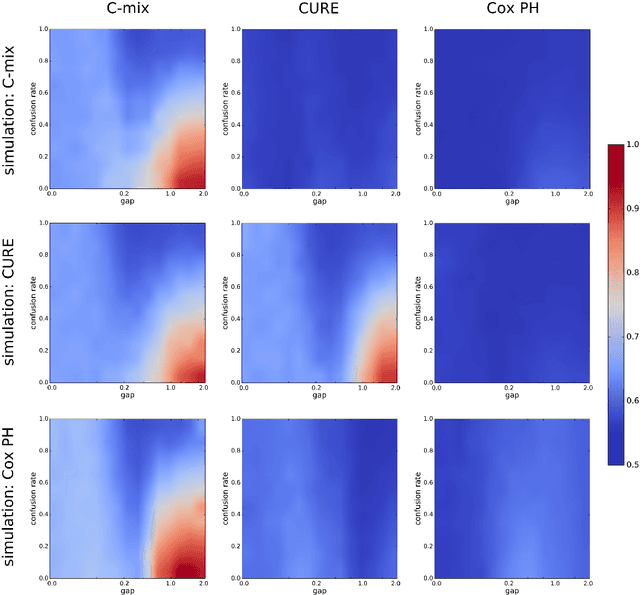
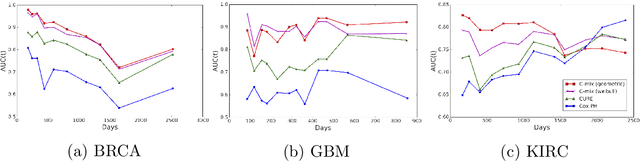
We introduce a mixture model for censored durations (C-mix), and develop maximum likelihood inference for the joint estimation of the time distributions and latent regression parameters of the model. We consider a high-dimensional setting, with datasets containing a large number of biomedical covariates. We therefore penalize the negative log-likelihood by the Elastic-Net, which leads to a sparse parameterization of the model. Inference is achieved using an efficient Quasi-Newton Expectation Maximization (QNEM) algorithm, for which we provide convergence properties. We then propose a score by assessing the patients risk of early adverse event. The statistical performance of the method is examined on an extensive Monte Carlo simulation study, and finally illustrated on three genetic datasets with high-dimensional covariates. We show that our approach outperforms the state-of-the-art, namely both the CURE and Cox proportional hazards models for this task, both in terms of C-index and AUC(t).

Binarsity: a penalization for one-hot encoded features

This paper deals with the problem of large-scale linear supervised learning in settings where a large number of continuous features are available. We propose to combine the well-known trick of one-hot encoding of continuous features with a new penalization called binarsity. In each group of binary features coming from the one-hot encoding of a single raw continuous feature, this penalization uses total-variation regularization together with an extra linear constraint to avoid collinearity within groups. Non-asymptotic oracle inequalities for generalized linear models are proposed, and numerical experiments illustrate the good performances of our approach on several datasets. It is also noteworthy that our method has a numerical complexity comparable to standard $\ell_1$ penalization.