Dynamical Survival Analysis with Controlled Latent States

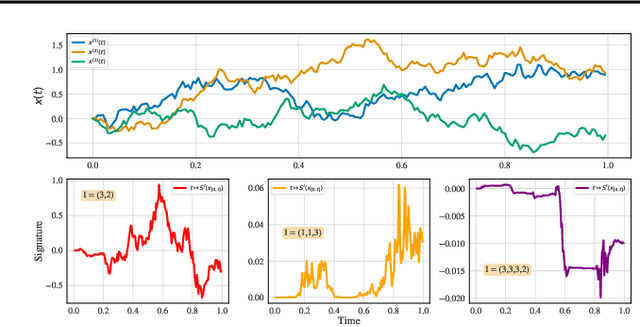
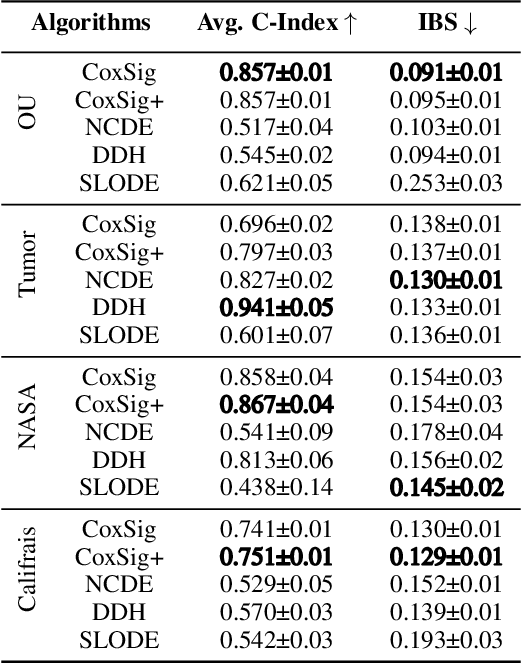
We consider the task of learning individual-specific intensities of counting processes from a set of static variables and irregularly sampled time series. We introduce a novel modelization approach in which the intensity is the solution to a controlled differential equation. We first design a neural estimator by building on neural controlled differential equations. In a second time, we show that our model can be linearized in the signature space under sufficient regularity conditions, yielding a signature-based estimator which we call CoxSig. We provide theoretical learning guarantees for both estimators, before showcasing the performance of our models on a vast array of simulated and real-world datasets from finance, predictive maintenance and food supply chain management.

On the Generalization Capacities of Neural Controlled Differential Equations

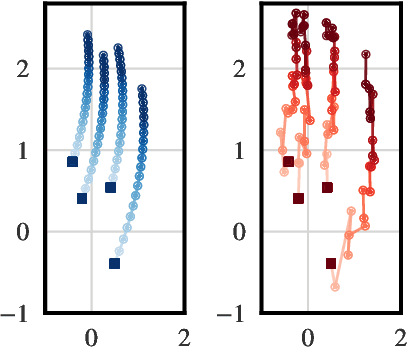
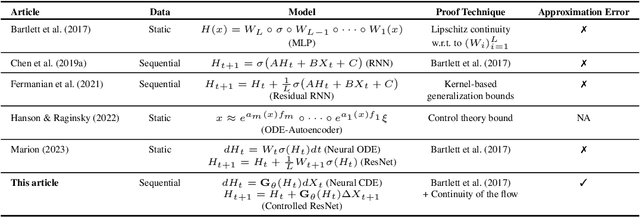
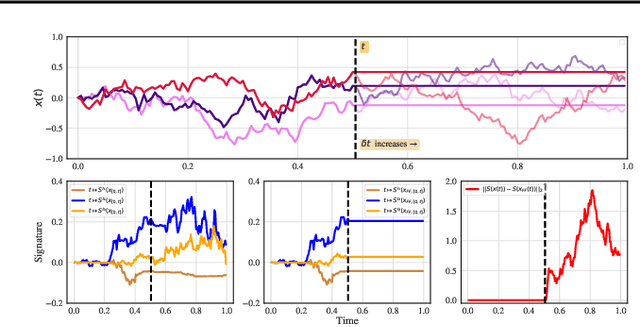
We consider a supervised learning setup in which the goal is to predicts an outcome from a sample of irregularly sampled time series using Neural Controlled Differential Equations (Kidger, Morrill, et al. 2020). In our framework, the time series is a discretization of an unobserved continuous path, and the outcome depends on this path through a controlled differential equation with unknown vector field. Learning with discrete data thus induces a discretization bias, which we precisely quantify. Using theoretical results on the continuity of the flow of controlled differential equations, we show that the approximation bias is directly related to the approximation error of a Lipschitz function defining the generative model by a shallow neural network. By combining these result with recent work linking the Lipschitz constant of neural networks to their generalization capacities, we upper bound the generalization gap between the expected loss attained by the empirical risk minimizer and the expected loss of the true predictor.

Learning the Dynamics of Sparsely Observed Interacting Systems

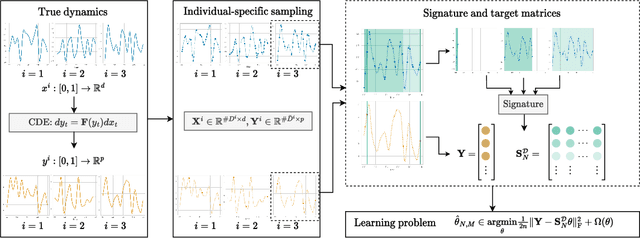
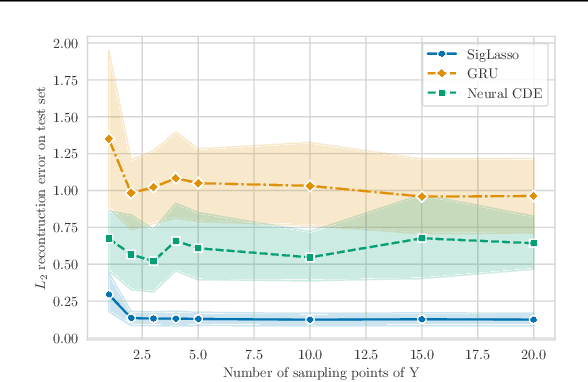
We address the problem of learning the dynamics of an unknown non-parametric system linking a target and a feature time series. The feature time series is measured on a sparse and irregular grid, while we have access to only a few points of the target time series. Once learned, we can use these dynamics to predict values of the target from the previous values of the feature time series. We frame this task as learning the solution map of a controlled differential equation (CDE). By leveraging the rich theory of signatures, we are able to cast this non-linear problem as a high-dimensional linear regression. We provide an oracle bound on the prediction error which exhibits explicit dependencies on the individual-specific sampling schemes. Our theoretical results are illustrated by simulations which show that our method outperforms existing algorithms for recovering the full time series while being computationally cheap. We conclude by demonstrating its potential on real-world epidemiological data.

SurvCaus : Representation Balancing for Survival Causal Inference

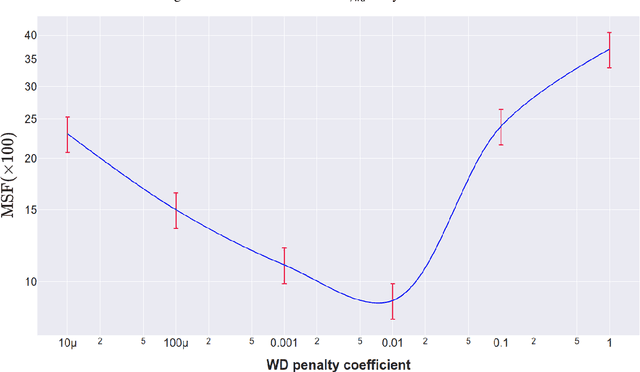
Individual Treatment Effects (ITE) estimation methods have risen in popularity in the last years. Most of the time, individual effects are better presented as Conditional Average Treatment Effects (CATE). Recently, representation balancing techniques have gained considerable momentum in causal inference from observational data, still limited to continuous (and binary) outcomes. However, in numerous pathologies, the outcome of interest is a (possibly censored) survival time. Our paper proposes theoretical guarantees for a representation balancing framework applied to counterfactual inference in a survival setting using a neural network capable of predicting the factual and counterfactual survival functions (and then the CATE), in the presence of censorship, at the individual level. We also present extensive experiments on synthetic and semisynthetic datasets that show that the proposed extensions outperform baseline methods.

Comparison of methods for early-readmission prediction in a high-dimensional heterogeneous covariates and time-to-event outcome framework

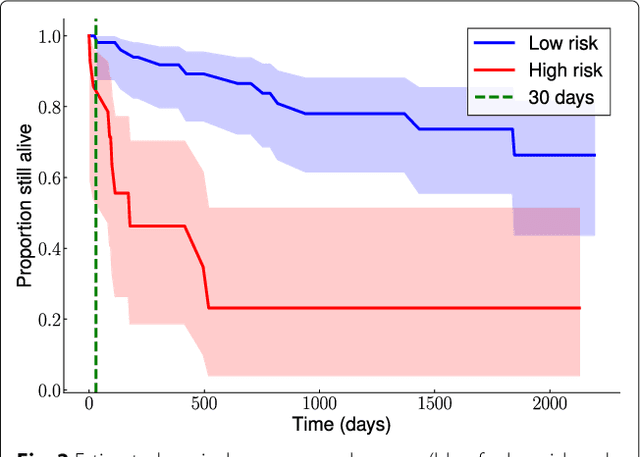
Background: Choosing the most performing method in terms of outcome prediction or variables selection is a recurring problem in prognosis studies, leading to many publications on methods comparison. But some aspects have received little attention. First, most comparison studies treat prediction performance and variable selection aspects separately. Second, methods are either compared within a binary outcome setting (based on an arbitrarily chosen delay) or within a survival setting, but not both. In this paper, we propose a comparison methodology to weight up those different settings both in terms of prediction and variables selection, while incorporating advanced machine learning strategies. Methods: Using a high-dimensional case study on a sickle-cell disease (SCD) cohort, we compare 8 statistical methods. In the binary outcome setting, we consider logistic regression (LR), support vector machine (SVM), random forest (RF), gradient boosting (GB) and neural network (NN); while on the survival analysis setting, we consider the Cox Proportional Hazards (PH), the CURE and the C-mix models. We then compare performances of all methods both in terms of risk prediction and variable selection, with a focus on the use of Elastic-Net regularization technique. Results: Among all assessed statistical methods assessed, the C-mix model yields the better performances in both the two considered settings, as well as interesting interpretation aspects. There is some consistency in selected covariates across methods within a setting, but not much across the two settings. Conclusions: It appears that learning withing the survival setting first, and then going back to a binary prediction using the survival estimates significantly enhance binary predictions.

Binacox: automatic cut-points detection in high-dimensional Cox model, with applications to genetic data

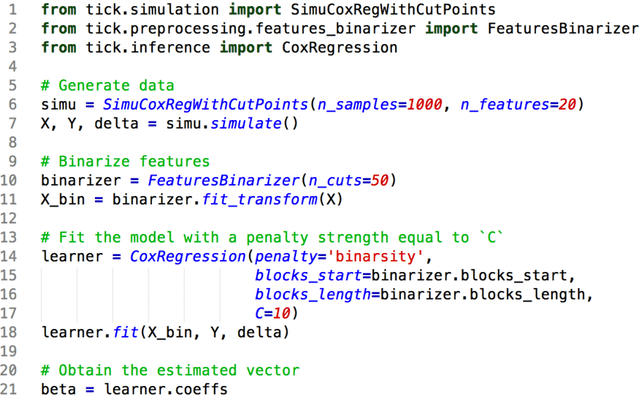
Determining significant prognostic biomarkers is of increasing importance in many areas of medicine. In order to translate a continuous biomarker into a clinical decision, it is often necessary to determine cut-points. There is so far no standard method to help evaluate how many cut-points are optimal for a given feature in a survival analysis setting. Moreover, most existing methods are univariate, hence not well suited for high-dimensional frameworks. This paper introduces a prognostic method called Binacox to deal with the problem of detecting multiple cut-points per features in a multivariate setting where a large number of continuous features are available. It is based on the Cox model and combines one-hot encodings with the binarsity penalty. This penalty uses total-variation regularization together with an extra linear constraint to avoid collinearity between the one-hot encodings and enable feature selection. A non-asymptotic oracle inequality is established. The statistical performance of the method is then examined on an extensive Monte Carlo simulation study, and finally illustrated on three publicly available genetic cancer datasets with high-dimensional features. On this datasets, our proposed methodology significantly outperforms the state-of-the-art survival models regarding risk prediction in terms of C-index, with a computing time orders of magnitude faster. In addition, it provides powerful interpretability by automatically pinpointing significant cut-points on relevant features from a clinical point of view.

ConvSCCS: convolutional self-controlled case series model for lagged adverse event detection

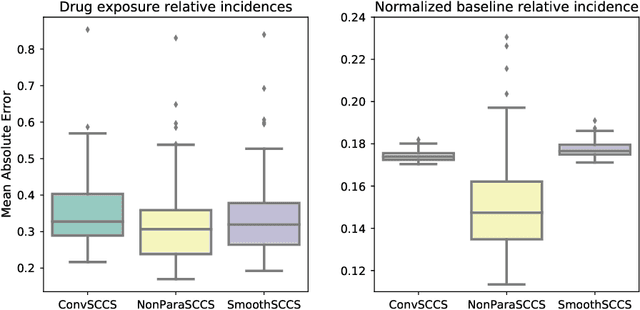
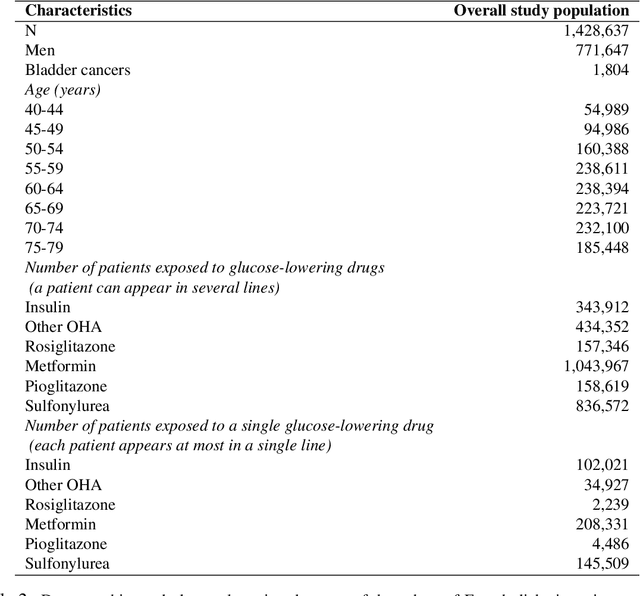
With the increased availability of large databases of electronic health records (EHRs) comes the chance of enhancing health risks screening. Most post-marketing detections of adverse drug reaction (ADR) rely on physicians' spontaneous reports, leading to under reporting. To take up this challenge, we develop a scalable model to estimate the effect of multiple longitudinal features (drug exposures) on a rare longitudinal outcome. Our procedure is based on a conditional Poisson model also known as self-controlled case series (SCCS). We model the intensity of outcomes using a convolution between exposures and step functions, that are penalized using a combination of group-Lasso and total-variation. This approach does not require the specification of precise risk periods, and allows to study in the same model several exposures at the same time. We illustrate the fact that this approach improves the state-of-the-art for the estimation of the relative risks both on simulations and on a cohort of diabetic patients, extracted from the large French national health insurance database (SNIIRAM), a SQL database built around medical reimbursements of more than 65 million people. This work has been done in the context of a research partnership between Ecole Polytechnique and CNAMTS (in charge of SNIIRAM).

High-dimensional robust regression and outliers detection with SLOPE

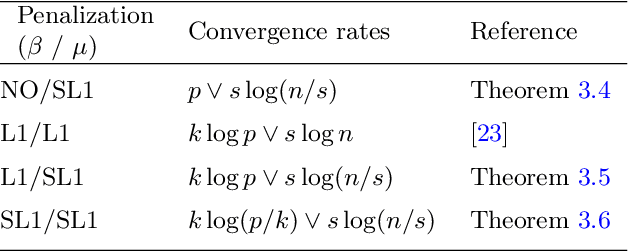
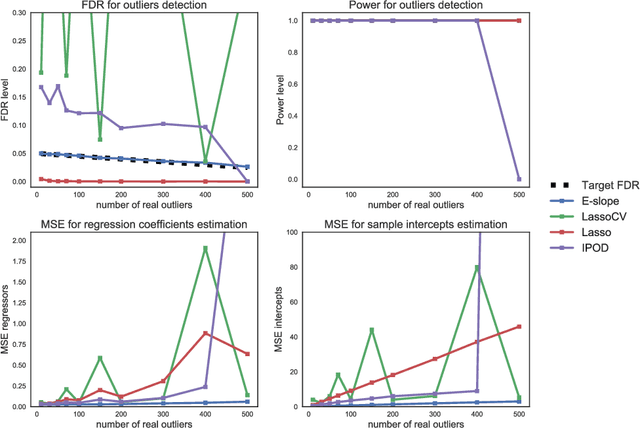
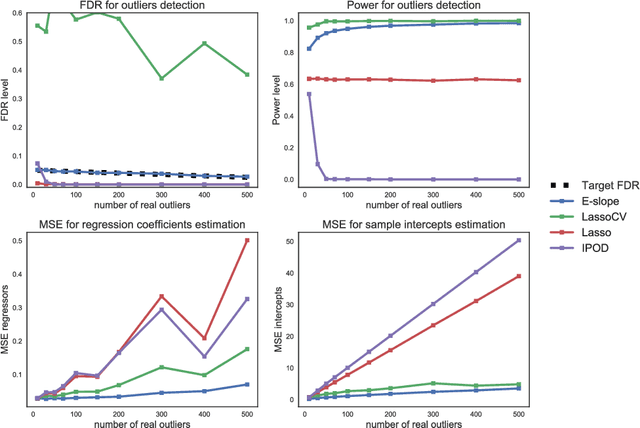
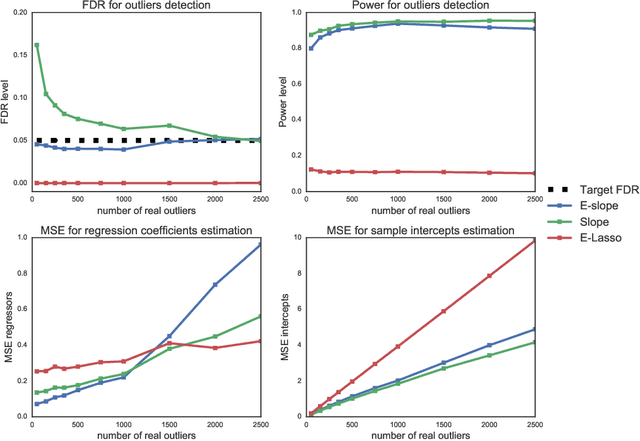
The problems of outliers detection and robust regression in a high-dimensional setting are fundamental in statistics, and have numerous applications. Following a recent set of works providing methods for simultaneous robust regression and outliers detection, we consider in this paper a model of linear regression with individual intercepts, in a high-dimensional setting. We introduce a new procedure for simultaneous estimation of the linear regression coefficients and intercepts, using two dedicated sorted-$\ell_1$ penalizations, also called SLOPE. We develop a complete theory for this problem: first, we provide sharp upper bounds on the statistical estimation error of both the vector of individual intercepts and regression coefficients. Second, we give an asymptotic control on the False Discovery Rate (FDR) and statistical power for support selection of the individual intercepts. As a consequence, this paper is the first to introduce a procedure with guaranteed FDR and statistical power control for outliers detection under the mean-shift model. Numerical illustrations, with a comparison to recent alternative approaches, are provided on both simulated and several real-world datasets. Experiments are conducted using an open-source software written in Python and C++.

C-mix: a high dimensional mixture model for censored durations, with applications to genetic data

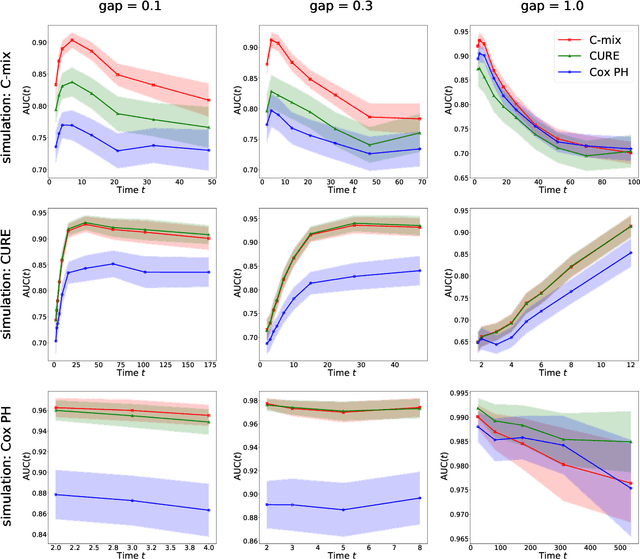
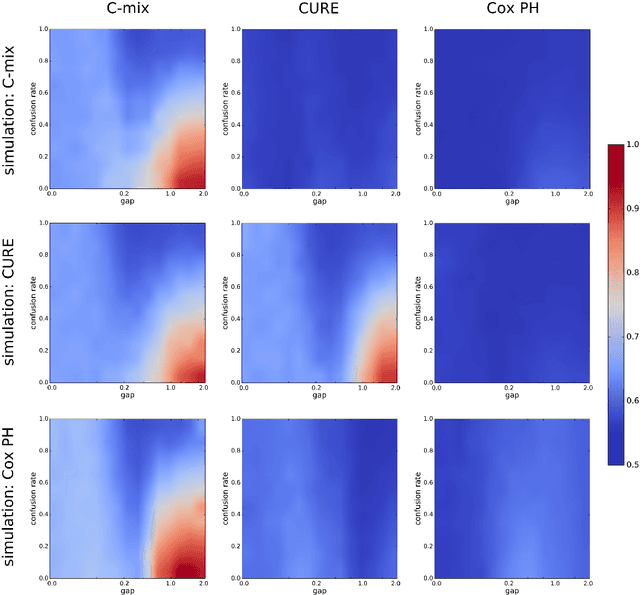
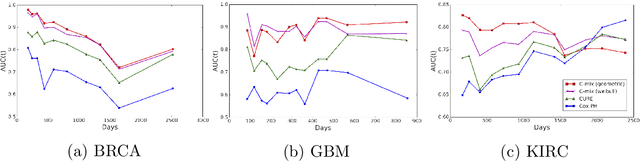
We introduce a mixture model for censored durations (C-mix), and develop maximum likelihood inference for the joint estimation of the time distributions and latent regression parameters of the model. We consider a high-dimensional setting, with datasets containing a large number of biomedical covariates. We therefore penalize the negative log-likelihood by the Elastic-Net, which leads to a sparse parameterization of the model. Inference is achieved using an efficient Quasi-Newton Expectation Maximization (QNEM) algorithm, for which we provide convergence properties. We then propose a score by assessing the patients risk of early adverse event. The statistical performance of the method is examined on an extensive Monte Carlo simulation study, and finally illustrated on three genetic datasets with high-dimensional covariates. We show that our approach outperforms the state-of-the-art, namely both the CURE and Cox proportional hazards models for this task, both in terms of C-index and AUC(t).

Binarsity: a penalization for one-hot encoded features

This paper deals with the problem of large-scale linear supervised learning in settings where a large number of continuous features are available. We propose to combine the well-known trick of one-hot encoding of continuous features with a new penalization called binarsity. In each group of binary features coming from the one-hot encoding of a single raw continuous feature, this penalization uses total-variation regularization together with an extra linear constraint to avoid collinearity within groups. Non-asymptotic oracle inequalities for generalized linear models are proposed, and numerical experiments illustrate the good performances of our approach on several datasets. It is also noteworthy that our method has a numerical complexity comparable to standard $\ell_1$ penalization.