Structure Learning of Gaussian Markov Random Fields with False Discovery Rate Control

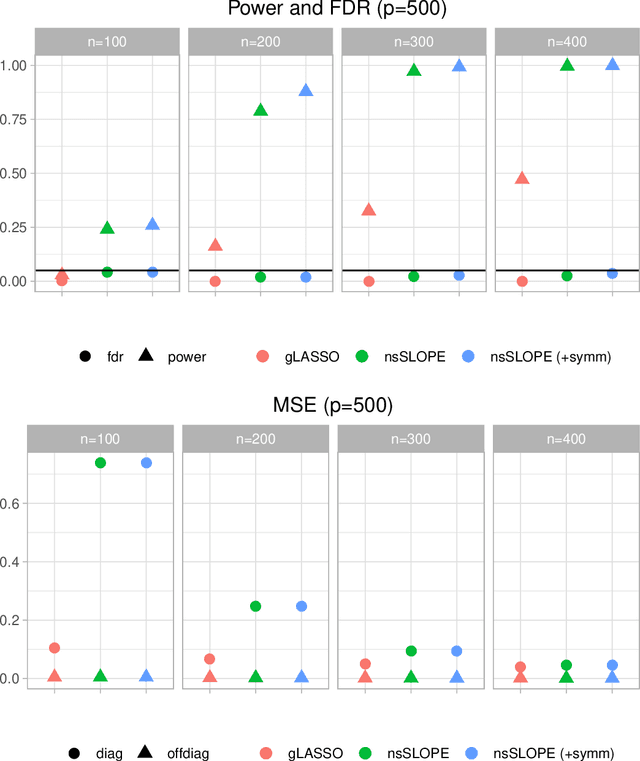
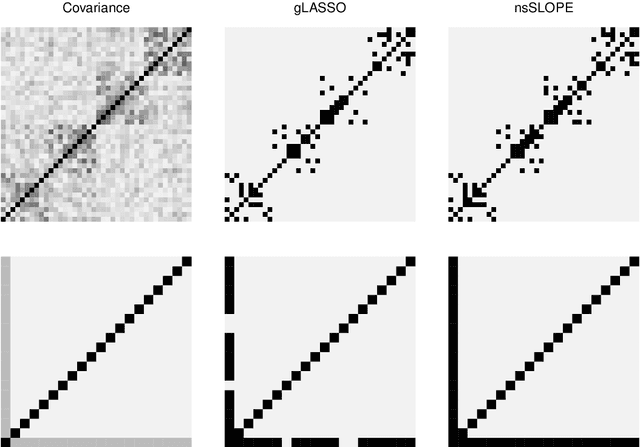
In this paper, we propose a new estimation procedure for discovering the structure of Gaussian Markov random fields (MRFs) with false discovery rate (FDR) control, making use of the sorted l1-norm (SL1) regularization. A Gaussian MRF is an acyclic graph representing a multivariate Gaussian distribution, where nodes are random variables and edges represent the conditional dependence between the connected nodes. Since it is possible to learn the edge structure of Gaussian MRFs directly from data, Gaussian MRFs provide an excellent way to understand complex data by revealing the dependence structure among many inputs features, such as genes, sensors, users, documents, etc. In learning the graphical structure of Gaussian MRFs, it is desired to discover the actual edges of the underlying but unknown probabilistic graphical model-it becomes more complicated when the number of random variables (features) p increases, compared to the number of data points n. In particular, when p >> n, it is statistically unavoidable for any estimation procedure to include false edges. Therefore, there have been many trials to reduce the false detection of edges, in particular, using different types of regularization on the learning parameters. Our method makes use of the SL1 regularization, introduced recently for model selection in linear regression. We focus on the benefit of SL1 regularization that it can be used to control the FDR of detecting important random variables. Adapting SL1 for probabilistic graphical models, we show that SL1 can be used for the structure learning of Gaussian MRFs using our suggested procedure nsSLOPE (neighborhood selection Sorted L-One Penalized Estimation), controlling the FDR of detecting edges.

High-dimensional robust regression and outliers detection with SLOPE

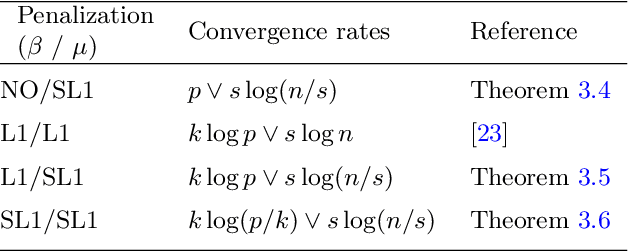
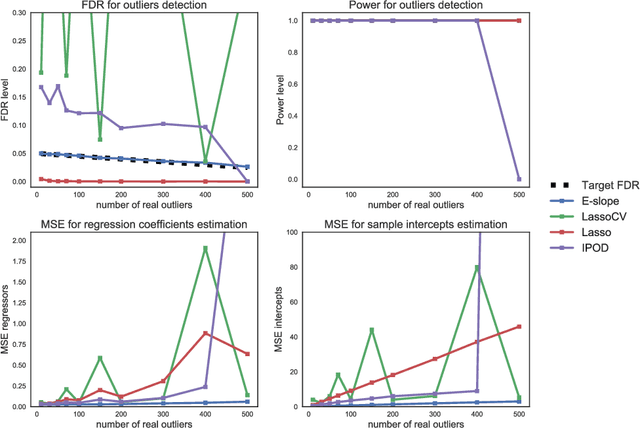
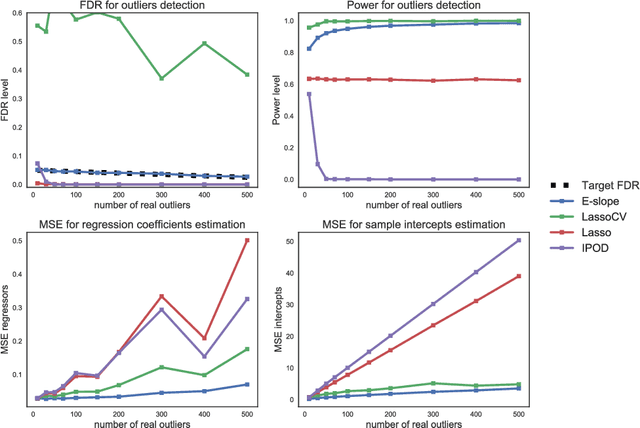
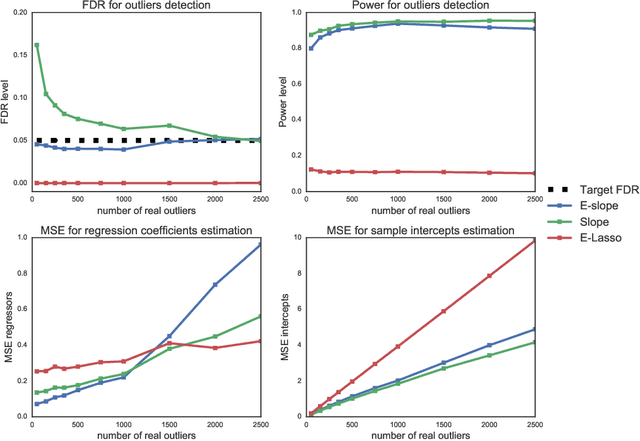
The problems of outliers detection and robust regression in a high-dimensional setting are fundamental in statistics, and have numerous applications. Following a recent set of works providing methods for simultaneous robust regression and outliers detection, we consider in this paper a model of linear regression with individual intercepts, in a high-dimensional setting. We introduce a new procedure for simultaneous estimation of the linear regression coefficients and intercepts, using two dedicated sorted-$\ell_1$ penalizations, also called SLOPE. We develop a complete theory for this problem: first, we provide sharp upper bounds on the statistical estimation error of both the vector of individual intercepts and regression coefficients. Second, we give an asymptotic control on the False Discovery Rate (FDR) and statistical power for support selection of the individual intercepts. As a consequence, this paper is the first to introduce a procedure with guaranteed FDR and statistical power control for outliers detection under the mean-shift model. Numerical illustrations, with a comparison to recent alternative approaches, are provided on both simulated and several real-world datasets. Experiments are conducted using an open-source software written in Python and C++.

False Discoveries Occur Early on the Lasso Path

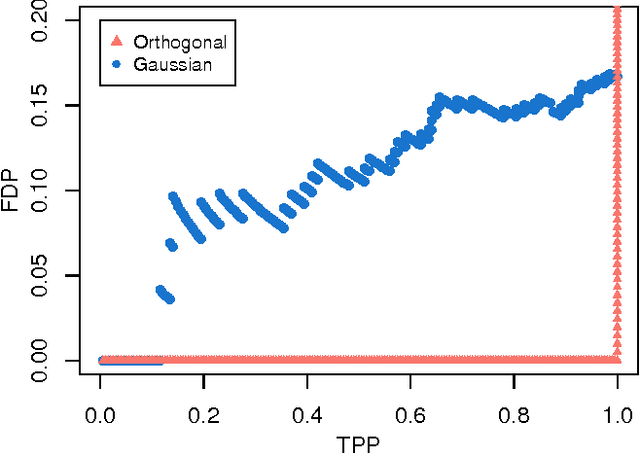
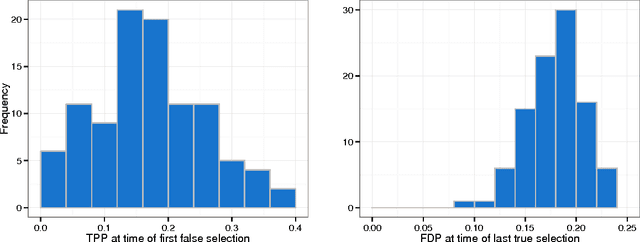
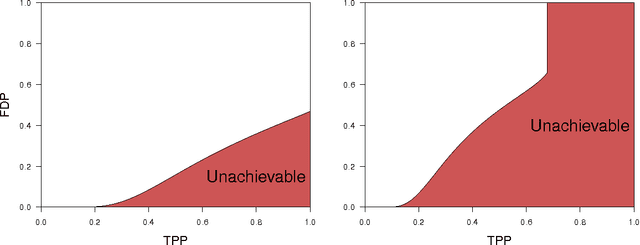
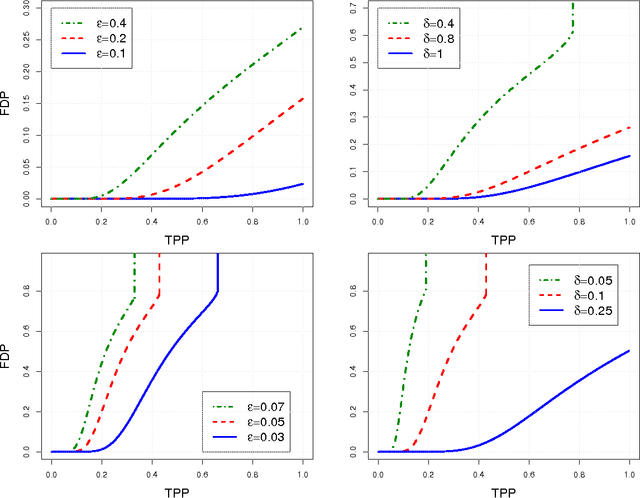
In regression settings where explanatory variables have very low correlations and there are relatively few effects, each of large magnitude, we expect the Lasso to find the important variables with few errors, if any. This paper shows that in a regime of linear sparsity---meaning that the fraction of variables with a non-vanishing effect tends to a constant, however small---this cannot really be the case, even when the design variables are stochastically independent. We demonstrate that true features and null features are always interspersed on the Lasso path, and that this phenomenon occurs no matter how strong the effect sizes are. We derive a sharp asymptotic trade-off between false and true positive rates or, equivalently, between measures of type I and type II errors along the Lasso path. This trade-off states that if we ever want to achieve a type II error (false negative rate) under a critical value, then anywhere on the Lasso path the type I error (false positive rate) will need to exceed a given threshold so that we can never have both errors at a low level at the same time. Our analysis uses tools from approximate message passing (AMP) theory as well as novel elements to deal with a possibly adaptive selection of the Lasso regularizing parameter.

Fast Saddle-Point Algorithm for Generalized Dantzig Selector and FDR Control with the Ordered l1-Norm

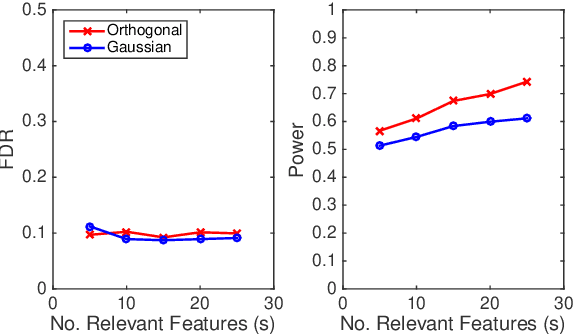
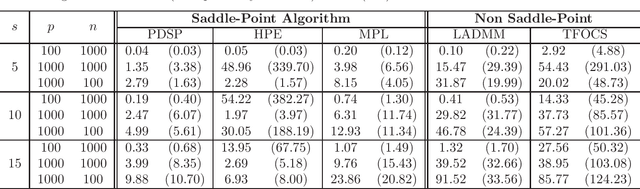
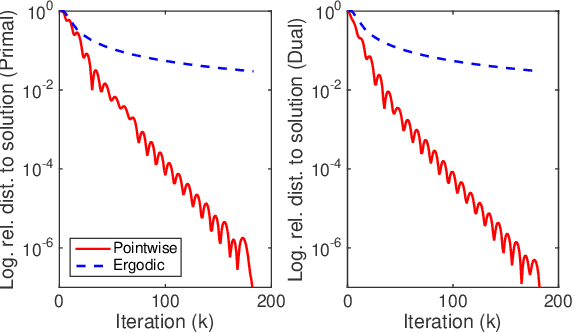
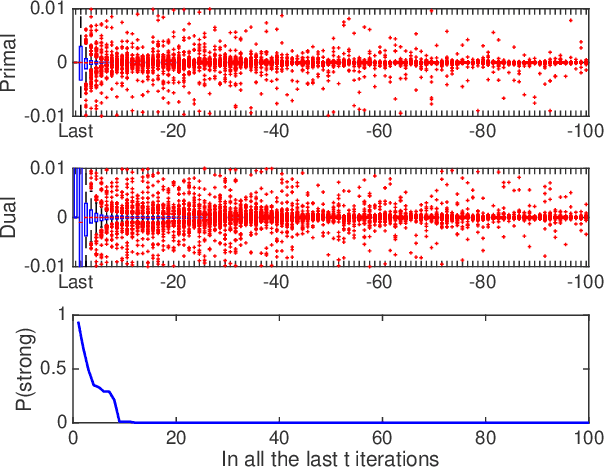
In this paper we propose a primal-dual proximal extragradient algorithm to solve the generalized Dantzig selector (GDS) estimation problem, based on a new convex-concave saddle-point (SP) reformulation. Our new formulation makes it possible to adopt recent developments in saddle-point optimization, to achieve the optimal $O(1/k)$ rate of convergence. Compared to the optimal non-SP algorithms, ours do not require specification of sensitive parameters that affect algorithm performance or solution quality. We also provide a new analysis showing a possibility of local acceleration to achieve the rate of $O(1/k^2)$ in special cases even without strong convexity or strong smoothness. As an application, we propose a GDS equipped with the ordered $\ell_1$-norm, showing its false discovery rate control properties in variable selection. Algorithm performance is compared between ours and other alternatives, including the linearized ADMM, Nesterov's smoothing, Nemirovski's mirror-prox, and the accelerated hybrid proximal extragradient techniques.