Fast Saddle-Point Algorithm for Generalized Dantzig Selector and FDR Control with the Ordered l1-Norm
Paper and Code
Jun 02, 2016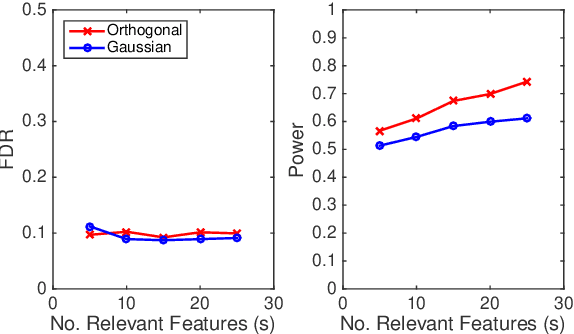
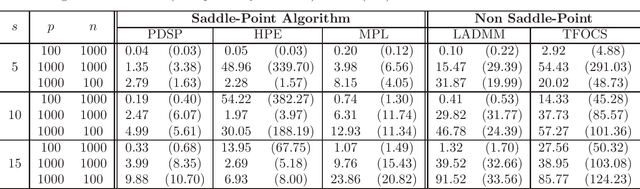
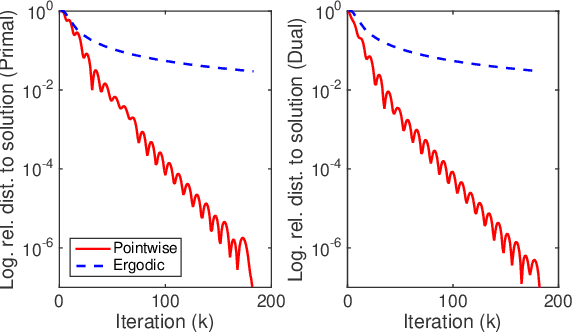
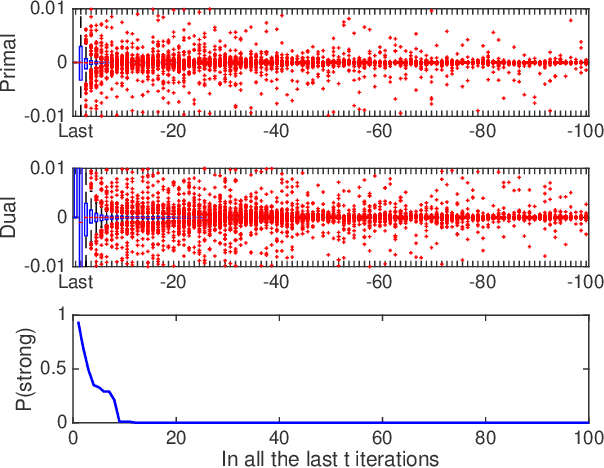
In this paper we propose a primal-dual proximal extragradient algorithm to solve the generalized Dantzig selector (GDS) estimation problem, based on a new convex-concave saddle-point (SP) reformulation. Our new formulation makes it possible to adopt recent developments in saddle-point optimization, to achieve the optimal $O(1/k)$ rate of convergence. Compared to the optimal non-SP algorithms, ours do not require specification of sensitive parameters that affect algorithm performance or solution quality. We also provide a new analysis showing a possibility of local acceleration to achieve the rate of $O(1/k^2)$ in special cases even without strong convexity or strong smoothness. As an application, we propose a GDS equipped with the ordered $\ell_1$-norm, showing its false discovery rate control properties in variable selection. Algorithm performance is compared between ours and other alternatives, including the linearized ADMM, Nesterov's smoothing, Nemirovski's mirror-prox, and the accelerated hybrid proximal extragradient techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge