Machine Learning and Statistical Approaches to Measuring Similarity of Political Parties

Mapping political party systems to metric policy spaces is one of the major methodological problems in political science. At present, in most political science project this task is performed by domain experts relying on purely qualitative assessments, with all the attendant problems of subjectivity and labor intensiveness. We consider how advances in natural language processing, including large transformer-based language models, can be applied to solve that issue. We apply a number of texts similarity measures to party political programs, analyze how they correlate with each other, and -- in the absence of a satisfactory benchmark -- evaluate them against other measures, including those based on expert surveys, voting records, electoral patterns, and candidate networks. Finally, we consider the prospects of relying on those methods to correct, supplement, and eventually replace expert judgments.

A Sparsity Inducing Nuclear-Norm Estimator (SpINNEr) for Matrix-Variate Regression in Brain Connectivity Analysis

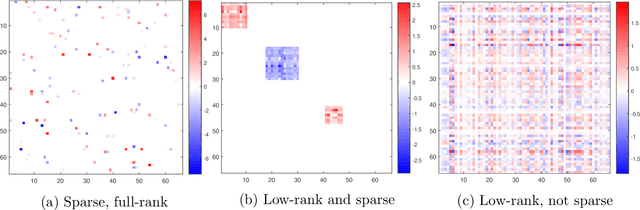
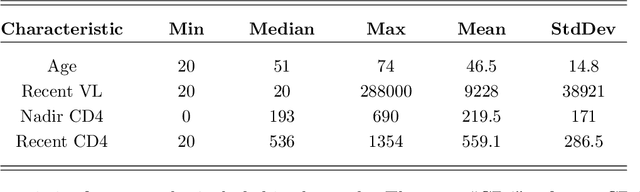
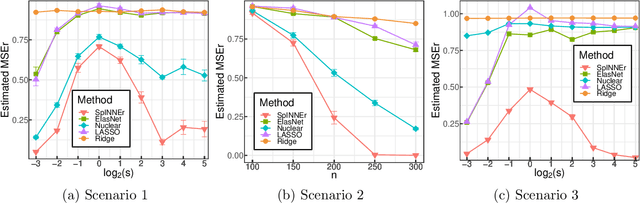
Classical scalar-response regression methods treat covariates as a vector and estimate a corresponding vector of regression coefficients. In medical applications, however, regressors are often in a form of multi-dimensional arrays. For example, one may be interested in using MRI imaging to identify which brain regions are associated with a health outcome. Vectorizing the two-dimensional image arrays is an unsatisfactory approach since it destroys the inherent spatial structure of the images and can be computationally challenging. We present an alternative approach - regularized matrix regression - where the matrix of regression coefficients is defined as a solution to the specific optimization problem. The method, called SParsity Inducing Nuclear Norm EstimatoR (SpINNEr), simultaneously imposes two penalty types on the regression coefficient matrix---the nuclear norm and the lasso norm---to encourage a low rank matrix solution that also has entry-wise sparsity. A specific implementation of the alternating direction method of multipliers (ADMM) is used to build a fast and efficient numerical solver. Our simulations show that SpINNEr outperforms other methods in estimation accuracy when the response-related entries (representing the brain's functional connectivity) are arranged in well-connected communities. SpINNEr is applied to investigate associations between HIV-related outcomes and functional connectivity in the human brain.

Fast Saddle-Point Algorithm for Generalized Dantzig Selector and FDR Control with the Ordered l1-Norm

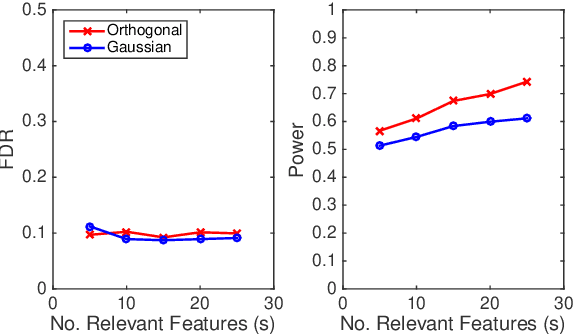
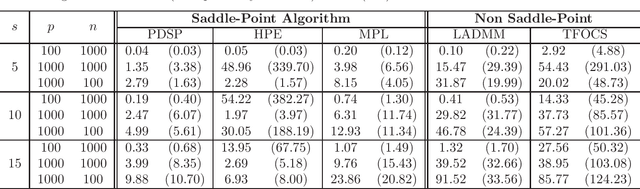
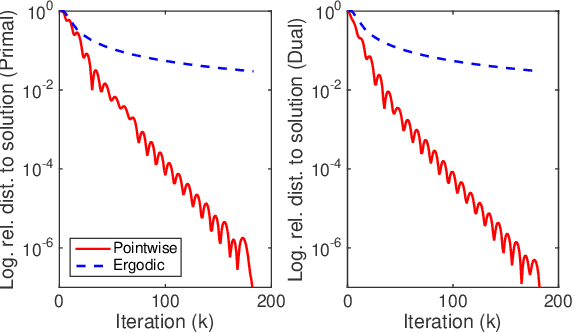
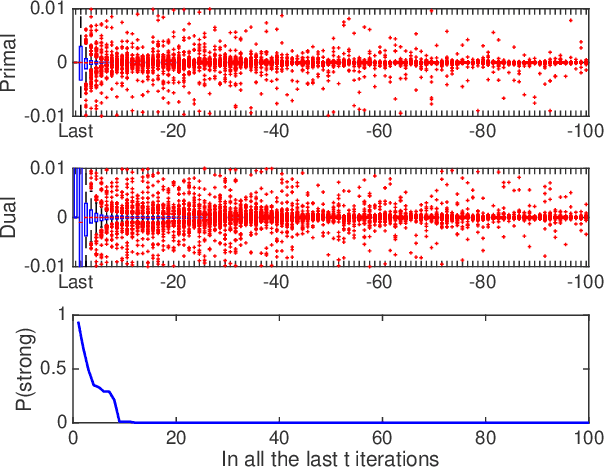
In this paper we propose a primal-dual proximal extragradient algorithm to solve the generalized Dantzig selector (GDS) estimation problem, based on a new convex-concave saddle-point (SP) reformulation. Our new formulation makes it possible to adopt recent developments in saddle-point optimization, to achieve the optimal $O(1/k)$ rate of convergence. Compared to the optimal non-SP algorithms, ours do not require specification of sensitive parameters that affect algorithm performance or solution quality. We also provide a new analysis showing a possibility of local acceleration to achieve the rate of $O(1/k^2)$ in special cases even without strong convexity or strong smoothness. As an application, we propose a GDS equipped with the ordered $\ell_1$-norm, showing its false discovery rate control properties in variable selection. Algorithm performance is compared between ours and other alternatives, including the linearized ADMM, Nesterov's smoothing, Nemirovski's mirror-prox, and the accelerated hybrid proximal extragradient techniques.