A Sparsity Inducing Nuclear-Norm Estimator (SpINNEr) for Matrix-Variate Regression in Brain Connectivity Analysis

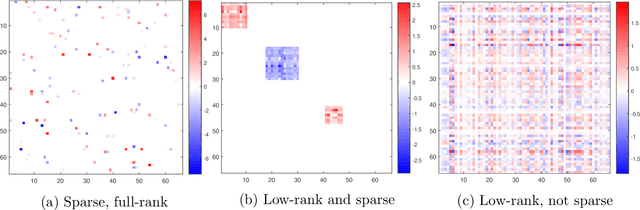
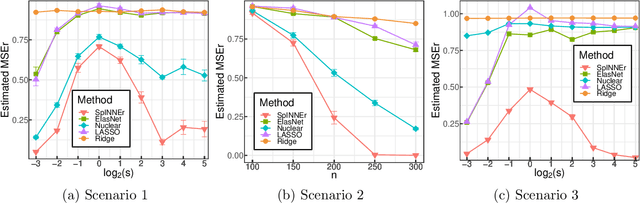
Classical scalar-response regression methods treat covariates as a vector and estimate a corresponding vector of regression coefficients. In medical applications, however, regressors are often in a form of multi-dimensional arrays. For example, one may be interested in using MRI imaging to identify which brain regions are associated with a health outcome. Vectorizing the two-dimensional image arrays is an unsatisfactory approach since it destroys the inherent spatial structure of the images and can be computationally challenging. We present an alternative approach - regularized matrix regression - where the matrix of regression coefficients is defined as a solution to the specific optimization problem. The method, called SParsity Inducing Nuclear Norm EstimatoR (SpINNEr), simultaneously imposes two penalty types on the regression coefficient matrix---the nuclear norm and the lasso norm---to encourage a low rank matrix solution that also has entry-wise sparsity. A specific implementation of the alternating direction method of multipliers (ADMM) is used to build a fast and efficient numerical solver. Our simulations show that SpINNEr outperforms other methods in estimation accuracy when the response-related entries (representing the brain's functional connectivity) are arranged in well-connected communities. SpINNEr is applied to investigate associations between HIV-related outcomes and functional connectivity in the human brain.

Regression Trees for Longitudinal Data

While studying response trajectory, often the population of interest may be diverse enough to exist distinct subgroups within it and the longitudinal change in response may not be uniform in these subgroups. That is, the timeslope and/or influence of covariates in longitudinal profile may vary among these different subgroups. For example, Raudenbush (2001) used depression as an example to argue that it is incorrect to assume that all the people in a given population would be experiencing either increasing or decreasing levels of depression. In such cases, traditional linear mixed effects model (assuming common parametric form for covariates and time) is not directly applicable for the entire population as a group-averaged trajectory can mask important subgroup differences. Our aim is to identify and characterize longitudinally homogeneous subgroups based on the combination of baseline covariates in the most parsimonious way. This goal can be achieved via constructing regression tree for longitudinal data using baseline covariates as partitioning variables. We have proposed LongCART algorithm to construct regression tree for the longitudinal data. In each node, the proposed LongCART algorithm determines the need for further splitting (i.e. whether parameter(s) of longitudinal profile is influenced by any baseline attributes) via parameter instability tests and thus the decision of further splitting is type-I error controlled. We have obtained the asymptotic results for the proposed instability test and examined finite sample behavior of the whole algorithm through simulation studies. Finally, we have applied the LongCART algorithm to study the longitudinal changes in choline level among HIV patients.