A Sparsity Inducing Nuclear-Norm Estimator (SpINNEr) for Matrix-Variate Regression in Brain Connectivity Analysis

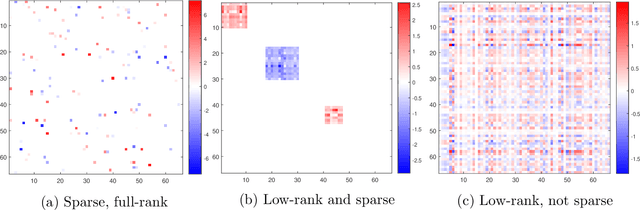
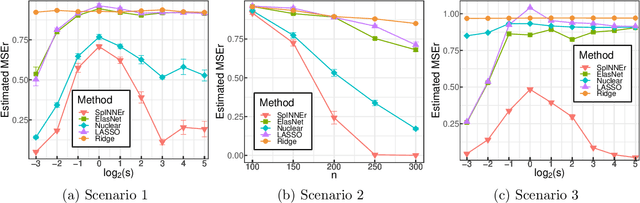
Classical scalar-response regression methods treat covariates as a vector and estimate a corresponding vector of regression coefficients. In medical applications, however, regressors are often in a form of multi-dimensional arrays. For example, one may be interested in using MRI imaging to identify which brain regions are associated with a health outcome. Vectorizing the two-dimensional image arrays is an unsatisfactory approach since it destroys the inherent spatial structure of the images and can be computationally challenging. We present an alternative approach - regularized matrix regression - where the matrix of regression coefficients is defined as a solution to the specific optimization problem. The method, called SParsity Inducing Nuclear Norm EstimatoR (SpINNEr), simultaneously imposes two penalty types on the regression coefficient matrix---the nuclear norm and the lasso norm---to encourage a low rank matrix solution that also has entry-wise sparsity. A specific implementation of the alternating direction method of multipliers (ADMM) is used to build a fast and efficient numerical solver. Our simulations show that SpINNEr outperforms other methods in estimation accuracy when the response-related entries (representing the brain's functional connectivity) are arranged in well-connected communities. SpINNEr is applied to investigate associations between HIV-related outcomes and functional connectivity in the human brain.

Incorporating Deep Features in the Analysis of Tissue Microarray Images

Tissue microarray (TMA) images have been used increasingly often in cancer studies and the validation of biomarkers. TACOMA---a cutting-edge automatic scoring algorithm for TMA images---is comparable to pathologists in terms of accuracy and repeatability. Here we consider how this algorithm may be further improved. Inspired by the recent success of deep learning, we propose to incorporate representations learnable through computation. We explore representations of a group nature through unsupervised learning, e.g., hierarchical clustering and recursive space partition. Information carried by clustering or spatial partitioning may be more concrete than the labels when the data are heterogeneous, or could help when the labels are noisy. The use of such information could be viewed as regularization in model fitting. It is motivated by major challenges in TMA image scoring---heterogeneity and label noise, and the cluster assumption in semi-supervised learning. Using this information on TMA images of breast cancer, we have reduced the error rate of TACOMA by about 6%. Further simulations on synthetic data provide insights on when such representations would likely help. Although we focus on TMAs, learnable representations of this type are expected to be applicable in other settings.