Beau Ances
A Sparsity Inducing Nuclear-Norm Estimator (SpINNEr) for Matrix-Variate Regression in Brain Connectivity Analysis
Jan 30, 2020
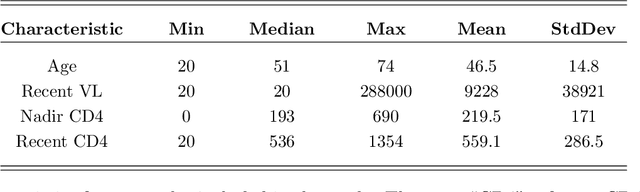

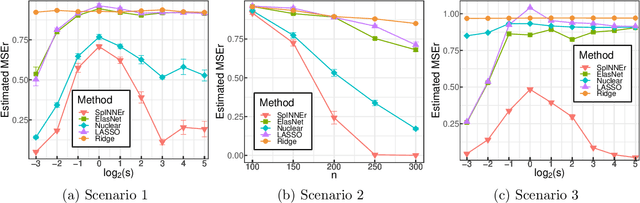
Abstract:Classical scalar-response regression methods treat covariates as a vector and estimate a corresponding vector of regression coefficients. In medical applications, however, regressors are often in a form of multi-dimensional arrays. For example, one may be interested in using MRI imaging to identify which brain regions are associated with a health outcome. Vectorizing the two-dimensional image arrays is an unsatisfactory approach since it destroys the inherent spatial structure of the images and can be computationally challenging. We present an alternative approach - regularized matrix regression - where the matrix of regression coefficients is defined as a solution to the specific optimization problem. The method, called SParsity Inducing Nuclear Norm EstimatoR (SpINNEr), simultaneously imposes two penalty types on the regression coefficient matrix---the nuclear norm and the lasso norm---to encourage a low rank matrix solution that also has entry-wise sparsity. A specific implementation of the alternating direction method of multipliers (ADMM) is used to build a fast and efficient numerical solver. Our simulations show that SpINNEr outperforms other methods in estimation accuracy when the response-related entries (representing the brain's functional connectivity) are arranged in well-connected communities. SpINNEr is applied to investigate associations between HIV-related outcomes and functional connectivity in the human brain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge