A Deep Neural Network Based Approach to Building Budget-Constrained Models for Big Data Analysis

Deep learning approaches require collection of data on many different input features or variables for accurate model training and prediction. Since data collection on input features could be costly, it is crucial to reduce the cost by selecting a subset of features and developing a budget-constrained model (BCM). In this paper, we introduce an approach to eliminating less important features for big data analysis using Deep Neural Networks (DNNs). Once a DNN model has been developed, we identify the weak links and weak neurons, and remove some input features to bring the model cost within a given budget. The experimental results show our approach is feasible and supports user selection of a suitable BCM within a given budget.

Improving Short Text Classification With Augmented Data Using GPT-3

GPT-3 is a large-scale natural language model developed by OpenAI that can perform many different tasks, including topic classification. Although researchers claim that it requires only a small number of in-context examples to learn a task, in practice GPT-3 requires these training examples to be either of exceptional quality or a higher quantity than easily created by hand. To address this issue, this study teaches GPT-3 to classify whether a question is related to data science by augmenting a small training set with additional examples generated by GPT-3 itself. This study compares two classifiers: the GPT-3 Classification Endpoint with augmented examples, and the GPT-3 Completion Endpoint with an optimal training set chosen using a genetic algorithm. We find that while the augmented Completion Endpoint achieves upwards of 80 percent validation accuracy, using the augmented Classification Endpoint yields more consistent accuracy on unseen examples. In this way, giving large-scale machine learning models like GPT-3 the ability to propose their own additional training examples can result in improved classification performance.

Learning Low-dimensional Manifolds for Scoring of Tissue Microarray Images

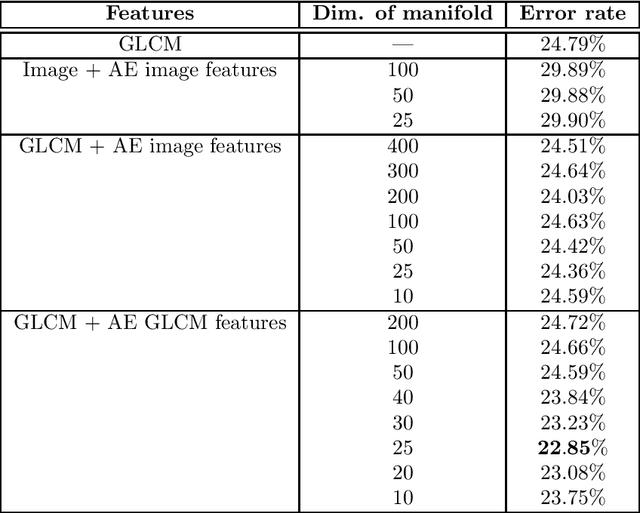
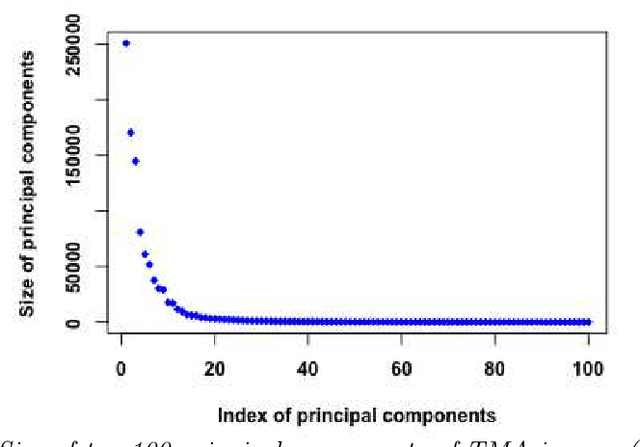
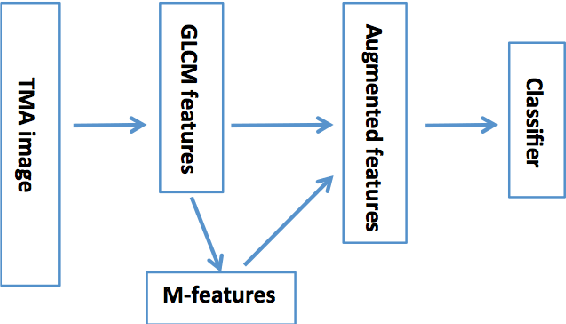
Tissue microarray (TMA) images have emerged as an important high-throughput tool for cancer study and the validation of biomarkers. Efforts have been dedicated to further improve the accuracy of TACOMA, a cutting-edge automatic scoring algorithm for TMA images. One major advance is due to deepTacoma, an algorithm that incorporates suitable deep representations of a group nature. Inspired by the recent advance in semi-supervised learning and deep learning, we propose mfTacoma to learn alternative deep representations in the context of TMA image scoring. In particular, mfTacoma learns the low-dimensional manifolds, a common latent structure in high dimensional data. Deep representation learning and manifold learning typically requires large data. By encoding deep representation of the manifolds as regularizing features, mfTacoma effectively leverages the manifold information that is potentially crude due to small data. Our experiments show that deep features by manifolds outperforms two alternatives -- deep features by linear manifolds with principal component analysis or by leveraging the group property.

$DC^2$: A Divide-and-conquer Algorithm for Large-scale Kernel Learning with Application to Clustering

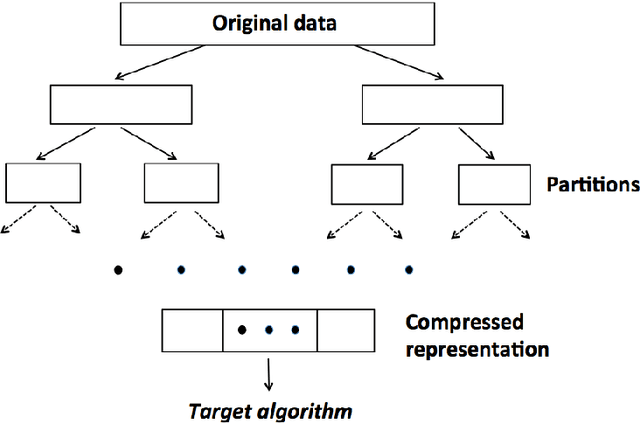
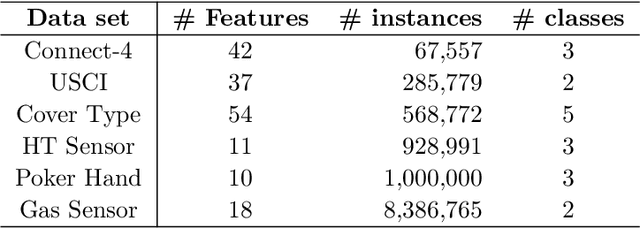
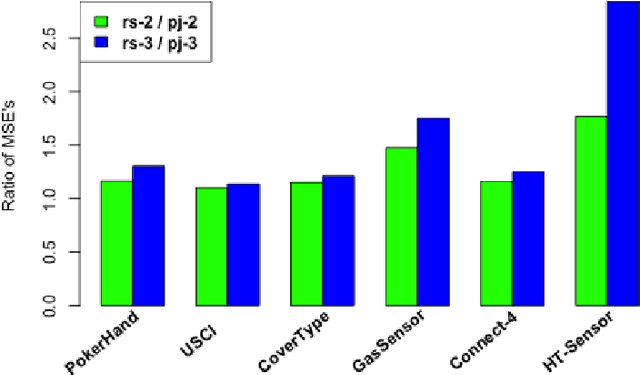
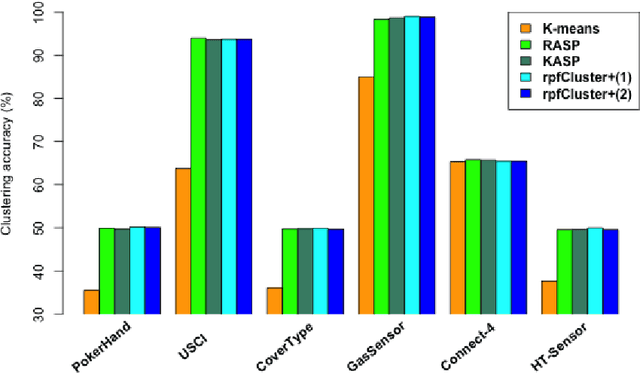
Divide-and-conquer is a general strategy to deal with large scale problems. It is typically applied to generate ensemble instances, which potentially limits the problem size it can handle. Additionally, the data are often divided by random sampling which may be suboptimal. To address these concerns, we propose the $DC^2$ algorithm. Instead of ensemble instances, we produce structure-preserving signature pieces to be assembled and conquered. $DC^2$ achieves the efficiency of sampling-based large scale kernel methods while enabling parallel multicore or clustered computation. The data partition and subsequent compression are unified by recursive random projections. Empirically dividing the data by random projections induces smaller mean squared approximation errors than conventional random sampling. The power of $DC^2$ is demonstrated by our clustering algorithm $rpfCluster^+$, which is as accurate as some fastest approximate spectral clustering algorithms while maintaining a running time close to that of K-means clustering. Analysis on $DC^2$ when applied to spectral clustering shows that the loss in clustering accuracy due to data division and reduction is upper bounded by the data approximation error which would vanish with recursive random projections. Due to its easy implementation and flexibility, we expect $DC^2$ to be applicable to general large scale learning problems.

Similarity Kernel and Clustering via Random Projection Forests

Similarity plays a fundamental role in many areas, including data mining, machine learning, statistics and various applied domains. Inspired by the success of ensemble methods and the flexibility of trees, we propose to learn a similarity kernel called rpf-kernel through random projection forests (rpForests). Our theoretical analysis reveals a highly desirable property of rpf-kernel: far-away (dissimilar) points have a low similarity value while nearby (similar) points would have a high similarity}, and the similarities have a native interpretation as the probability of points remaining in the same leaf nodes during the growth of rpForests. The learned rpf-kernel leads to an effective clustering algorithm--rpfCluster. On a wide variety of real and benchmark datasets, rpfCluster compares favorably to K-means clustering, spectral clustering and a state-of-the-art clustering ensemble algorithm--Cluster Forests. Our approach is simple to implement and readily adapt to the geometry of the underlying data. Given its desirable theoretical property and competitive empirical performance when applied to clustering, we expect rpf-kernel to be applicable to many problems of an unsupervised nature or as a regularizer in some supervised or weakly supervised settings.

Learning over inherently distributed data

The recent decades have seen a surge of interests in distributed computing. Existing work focus primarily on either distributed computing platforms, data query tools, or, algorithms to divide big data and conquer at individual machines etc. It is, however, increasingly often that the data of interest are inherently distributed, i.e., data are stored at multiple distributed sites due to diverse collection channels, business operations etc. We propose to enable learning and inference in such a setting via a general framework based on the distortion minimizing local transformations. This framework only requires a small amount of local signatures to be shared among distributed sites, eliminating the need of having to transmitting big data. Computation can be done very efficiently via parallel local computation. The error incurred due to distributed computing vanishes when increasing the size of local signatures. As the shared data need not be in their original form, data privacy may also be preserved. Experiments on linear (logistic) regression and Random Forests have shown promise of this approach. This framework is expected to apply to a general class of tools in learning and inference with the continuity property.

Fast communication-efficient spectral clustering over distributed data

The last decades have seen a surge of interests in distributed computing thanks to advances in clustered computing and big data technology. Existing distributed algorithms typically assume {\it all the data are already in one place}, and divide the data and conquer on multiple machines. However, it is increasingly often that the data are located at a number of distributed sites, and one wishes to compute over all the data with low communication overhead. For spectral clustering, we propose a novel framework that enables its computation over such distributed data, with "minimal" communications while a major speedup in computation. The loss in accuracy is negligible compared to the non-distributed setting. Our approach allows local parallel computing at where the data are located, thus turns the distributed nature of the data into a blessing; the speedup is most substantial when the data are evenly distributed across sites. Experiments on synthetic and large UC Irvine datasets show almost no loss in accuracy with our approach while about 2x speedup under various settings with two distributed sites. As the transmitted data need not be in their original form, our framework readily addresses the privacy concern for data sharing in distributed computing.

Cost-sensitive Selection of Variables by Ensemble of Model Sequences

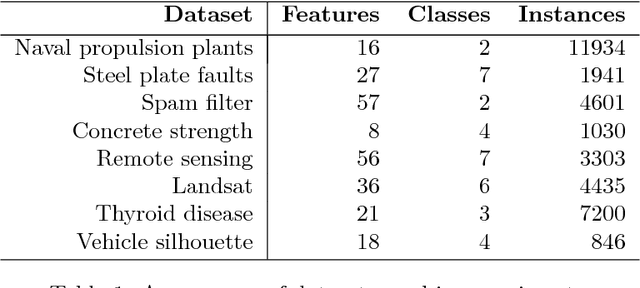
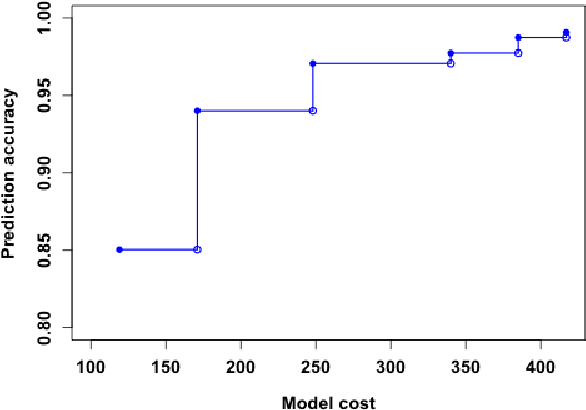
Many applications require the collection of data on different variables or measurements over many system performance metrics. We term those broadly as measures or variables. Often data collection along each measure incurs a cost, thus it is desirable to consider the cost of measures in modeling. This is a fairly new class of problems in the area of cost-sensitive learning. A few attempts have been made to incorporate costs in combining and selecting measures. However, existing studies either do not strictly enforce a budget constraint, or are not the `most' cost effective. With a focus on classification problem, we propose a computationally efficient approach that could find a near optimal model under a given budget by exploring the most `promising' part of the solution space. Instead of outputting a single model, we produce a model schedule---a list of models, sorted by model costs and expected predictive accuracy. This could be used to choose the model with the best predictive accuracy under a given budget, or to trade off between the budget and the predictive accuracy. Experiments on some benchmark datasets show that our approach compares favorably to competing methods.

K-nearest Neighbor Search by Random Projection Forests

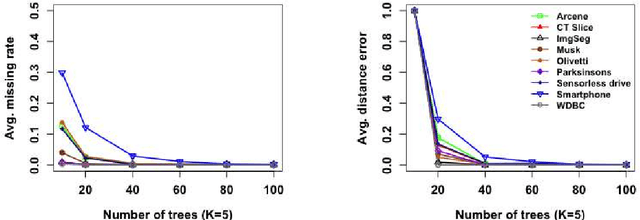
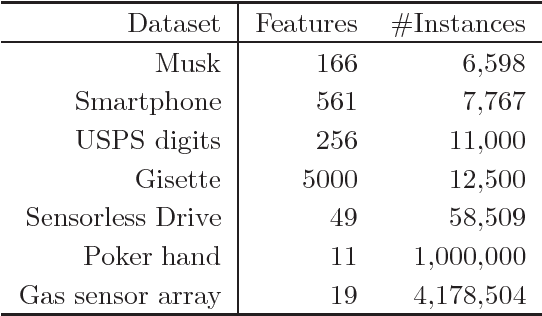
K-nearest neighbor (kNN) search has wide applications in many areas, including data mining, machine learning, statistics and many applied domains. Inspired by the success of ensemble methods and the flexibility of tree-based methodology, we propose random projection forests (rpForests), for kNN search. rpForests finds kNNs by aggregating results from an ensemble of random projection trees with each constructed recursively through a series of carefully chosen random projections. rpForests achieves a remarkable accuracy in terms of fast decay in the missing rate of kNNs and that of discrepancy in the kNN distances. rpForests has a very low computational complexity. The ensemble nature of rpForests makes it easily run in parallel on multicore or clustered computers; the running time is expected to be nearly inversely proportional to the number of cores or machines. We give theoretical insights by showing the exponential decay of the probability that neighboring points would be separated by ensemble random projection trees when the ensemble size increases. Our theory can be used to refine the choice of random projections in the growth of trees, and experiments show that the effect is remarkable.

Incorporating Deep Features in the Analysis of Tissue Microarray Images

Tissue microarray (TMA) images have been used increasingly often in cancer studies and the validation of biomarkers. TACOMA---a cutting-edge automatic scoring algorithm for TMA images---is comparable to pathologists in terms of accuracy and repeatability. Here we consider how this algorithm may be further improved. Inspired by the recent success of deep learning, we propose to incorporate representations learnable through computation. We explore representations of a group nature through unsupervised learning, e.g., hierarchical clustering and recursive space partition. Information carried by clustering or spatial partitioning may be more concrete than the labels when the data are heterogeneous, or could help when the labels are noisy. The use of such information could be viewed as regularization in model fitting. It is motivated by major challenges in TMA image scoring---heterogeneity and label noise, and the cluster assumption in semi-supervised learning. Using this information on TMA images of breast cancer, we have reduced the error rate of TACOMA by about 6%. Further simulations on synthetic data provide insights on when such representations would likely help. Although we focus on TMAs, learnable representations of this type are expected to be applicable in other settings.