$DC^2$: A Divide-and-conquer Algorithm for Large-scale Kernel Learning with Application to Clustering
Paper and Code
Nov 16, 2019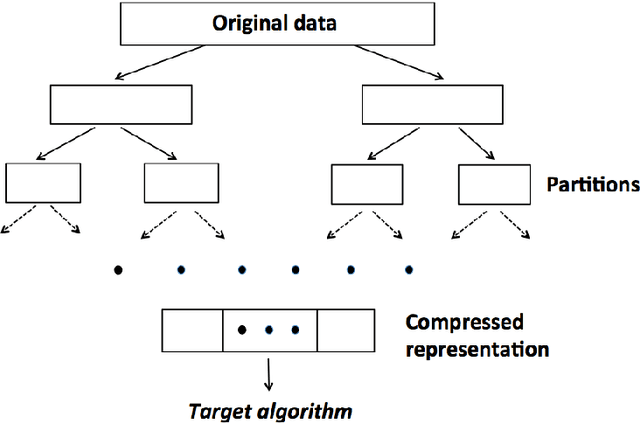
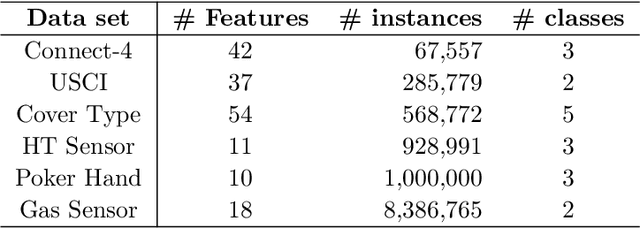
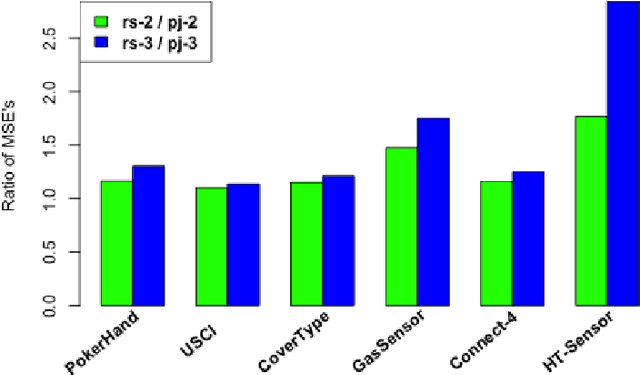
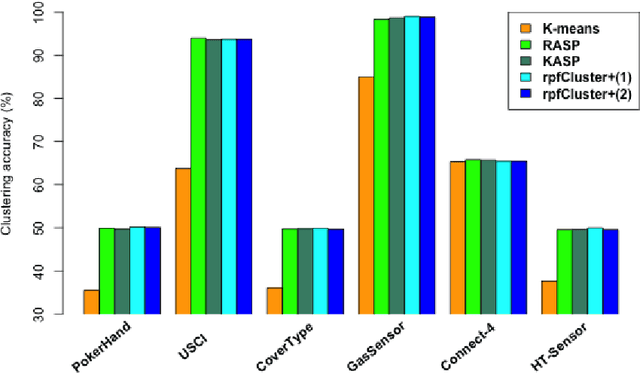
Divide-and-conquer is a general strategy to deal with large scale problems. It is typically applied to generate ensemble instances, which potentially limits the problem size it can handle. Additionally, the data are often divided by random sampling which may be suboptimal. To address these concerns, we propose the $DC^2$ algorithm. Instead of ensemble instances, we produce structure-preserving signature pieces to be assembled and conquered. $DC^2$ achieves the efficiency of sampling-based large scale kernel methods while enabling parallel multicore or clustered computation. The data partition and subsequent compression are unified by recursive random projections. Empirically dividing the data by random projections induces smaller mean squared approximation errors than conventional random sampling. The power of $DC^2$ is demonstrated by our clustering algorithm $rpfCluster^+$, which is as accurate as some fastest approximate spectral clustering algorithms while maintaining a running time close to that of K-means clustering. Analysis on $DC^2$ when applied to spectral clustering shows that the loss in clustering accuracy due to data division and reduction is upper bounded by the data approximation error which would vanish with recursive random projections. Due to its easy implementation and flexibility, we expect $DC^2$ to be applicable to general large scale learning problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge