Diffusion-Enhanced Test-time Adaptation with Text and Image Augmentation

Existing test-time prompt tuning (TPT) methods focus on single-modality data, primarily enhancing images and using confidence ratings to filter out inaccurate images. However, while image generation models can produce visually diverse images, single-modality data enhancement techniques still fail to capture the comprehensive knowledge provided by different modalities. Additionally, we note that the performance of TPT-based methods drops significantly when the number of augmented images is limited, which is not unusual given the computational expense of generative augmentation. To address these issues, we introduce IT3A, a novel test-time adaptation method that utilizes a pre-trained generative model for multi-modal augmentation of each test sample from unknown new domains. By combining augmented data from pre-trained vision and language models, we enhance the ability of the model to adapt to unknown new test data. Additionally, to ensure that key semantics are accurately retained when generating various visual and text enhancements, we employ cosine similarity filtering between the logits of the enhanced images and text with the original test data. This process allows us to filter out some spurious augmentation and inadequate combinations. To leverage the diverse enhancements provided by the generation model across different modals, we have replaced prompt tuning with an adapter for greater flexibility in utilizing text templates. Our experiments on the test datasets with distribution shifts and domain gaps show that in a zero-shot setting, IT3A outperforms state-of-the-art test-time prompt tuning methods with a 5.50% increase in accuracy.

UniM$^2$AE: Multi-modal Masked Autoencoders with Unified 3D Representation for 3D Perception in Autonomous Driving

Masked Autoencoders (MAE) play a pivotal role in learning potent representations, delivering outstanding results across various 3D perception tasks essential for autonomous driving. In real-world driving scenarios, it's commonplace to deploy multiple sensors for comprehensive environment perception. While integrating multi-modal features from these sensors can produce rich and powerful features, there is a noticeable gap in MAE methods addressing this integration. This research delves into multi-modal Masked Autoencoders tailored for a unified representation space in autonomous driving, aiming to pioneer a more efficient fusion of two distinct modalities. To intricately marry the semantics inherent in images with the geometric intricacies of LiDAR point clouds, the UniM$^2$AE is proposed. This model stands as a potent yet straightforward, multi-modal self-supervised pre-training framework, mainly consisting of two designs. First, it projects the features from both modalities into a cohesive 3D volume space, ingeniously expanded from the bird's eye view (BEV) to include the height dimension. The extension makes it possible to back-project the informative features, obtained by fusing features from both modalities, into their native modalities to reconstruct the multiple masked inputs. Second, the Multi-modal 3D Interactive Module (MMIM) is invoked to facilitate the efficient inter-modal interaction during the interaction process. Extensive experiments conducted on the nuScenes Dataset attest to the efficacy of UniM$^2$AE, indicating enhancements in 3D object detection and BEV map segmentation by 1.2\%(NDS) and 6.5\% (mIoU), respectively. Code is available at https://github.com/hollow-503/UniM2AE.

Learning Low-dimensional Manifolds for Scoring of Tissue Microarray Images

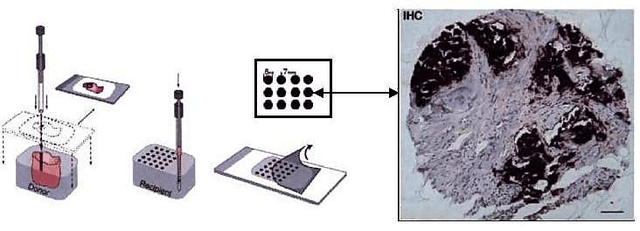
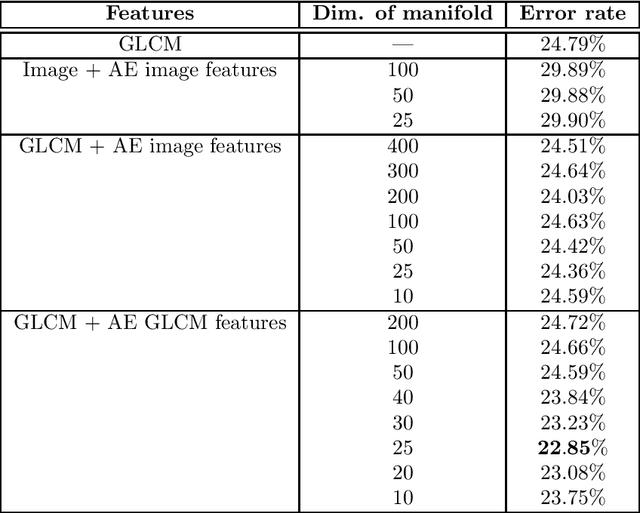
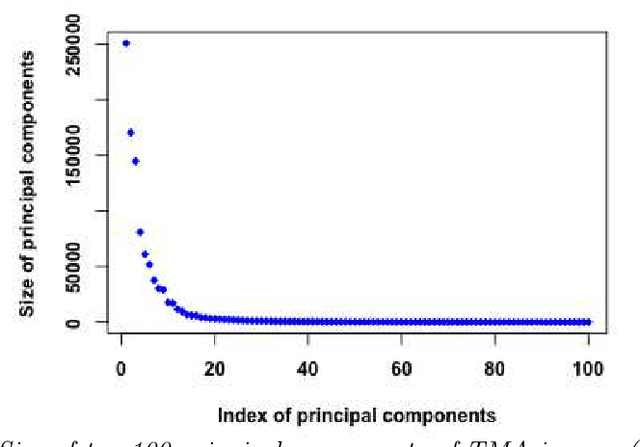
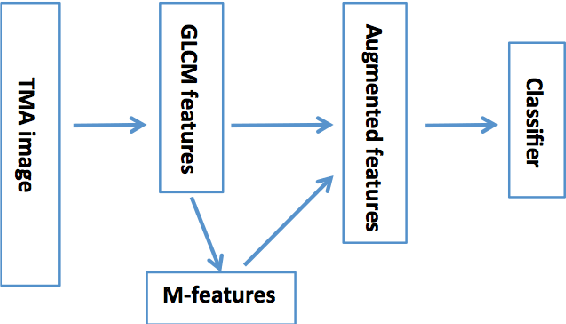
Tissue microarray (TMA) images have emerged as an important high-throughput tool for cancer study and the validation of biomarkers. Efforts have been dedicated to further improve the accuracy of TACOMA, a cutting-edge automatic scoring algorithm for TMA images. One major advance is due to deepTacoma, an algorithm that incorporates suitable deep representations of a group nature. Inspired by the recent advance in semi-supervised learning and deep learning, we propose mfTacoma to learn alternative deep representations in the context of TMA image scoring. In particular, mfTacoma learns the low-dimensional manifolds, a common latent structure in high dimensional data. Deep representation learning and manifold learning typically requires large data. By encoding deep representation of the manifolds as regularizing features, mfTacoma effectively leverages the manifold information that is potentially crude due to small data. Our experiments show that deep features by manifolds outperforms two alternatives -- deep features by linear manifolds with principal component analysis or by leveraging the group property.

Incorporating Deep Features in the Analysis of Tissue Microarray Images

Tissue microarray (TMA) images have been used increasingly often in cancer studies and the validation of biomarkers. TACOMA---a cutting-edge automatic scoring algorithm for TMA images---is comparable to pathologists in terms of accuracy and repeatability. Here we consider how this algorithm may be further improved. Inspired by the recent success of deep learning, we propose to incorporate representations learnable through computation. We explore representations of a group nature through unsupervised learning, e.g., hierarchical clustering and recursive space partition. Information carried by clustering or spatial partitioning may be more concrete than the labels when the data are heterogeneous, or could help when the labels are noisy. The use of such information could be viewed as regularization in model fitting. It is motivated by major challenges in TMA image scoring---heterogeneity and label noise, and the cluster assumption in semi-supervised learning. Using this information on TMA images of breast cancer, we have reduced the error rate of TACOMA by about 6%. Further simulations on synthetic data provide insights on when such representations would likely help. Although we focus on TMAs, learnable representations of this type are expected to be applicable in other settings.

Anomaly Detection via Graphical Lasso

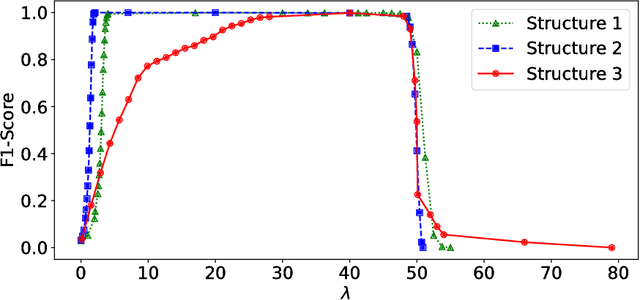
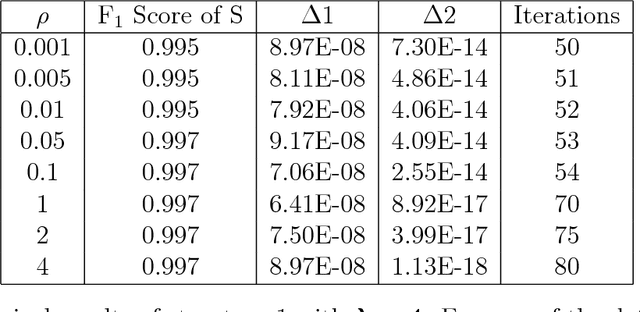
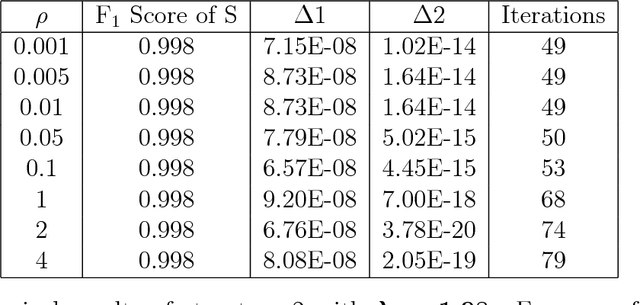
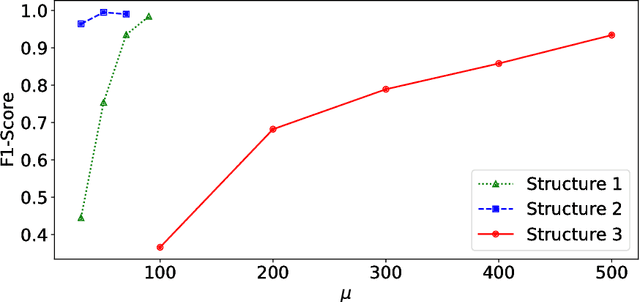
Anomalies and outliers are common in real-world data, and they can arise from many sources, such as sensor faults. Accordingly, anomaly detection is important both for analyzing the anomalies themselves and for cleaning the data for further analysis of its ambient structure. Nonetheless, a precise definition of anomalies is important for automated detection and herein we approach such problems from the perspective of detecting sparse latent effects embedded in large collections of noisy data. Standard Graphical Lasso-based techniques can identify the conditional dependency structure of a collection of random variables based on their sample covariance matrix. However, classic Graphical Lasso is sensitive to outliers in the sample covariance matrix. In particular, several outliers in a sample covariance matrix can destroy the sparsity of its inverse. Accordingly, we propose a novel optimization problem that is similar in spirit to Robust Principal Component Analysis (RPCA) and splits the sample covariance matrix $M$ into two parts, $M=F+S$, where $F$ is the cleaned sample covariance whose inverse is sparse and computable by Graphical Lasso, and $S$ contains the outliers in $M$. We accomplish this decomposition by adding an additional $ \ell_1$ penalty to classic Graphical Lasso, and name it "Robust Graphical Lasso (Rglasso)". Moreover, we propose an Alternating Direction Method of Multipliers (ADMM) solution to the optimization problem which scales to large numbers of unknowns. We evaluate our algorithm on both real and synthetic datasets, obtaining interpretable results and outperforming the standard robust Minimum Covariance Determinant (MCD) method and Robust Principal Component Analysis (RPCA) regarding both accuracy and speed.