ChemTime: Rapid and Early Classification for Multivariate Time Series Classification of Chemical Sensors

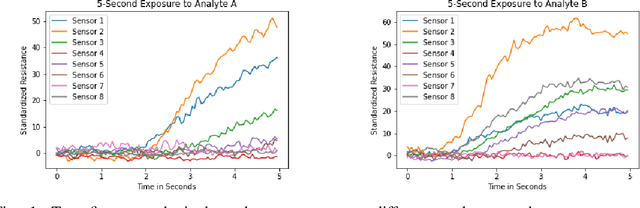
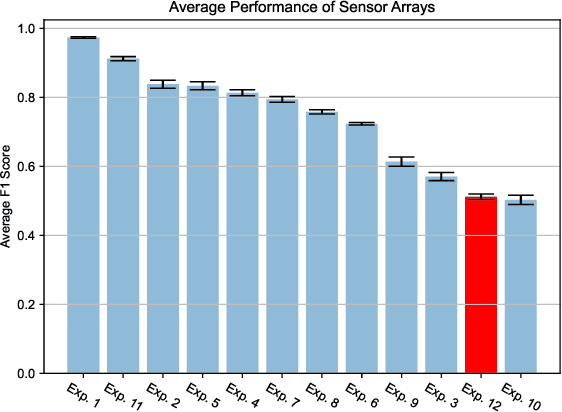
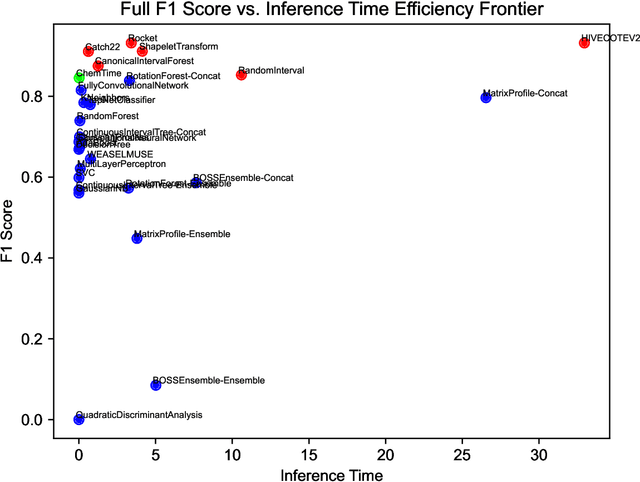
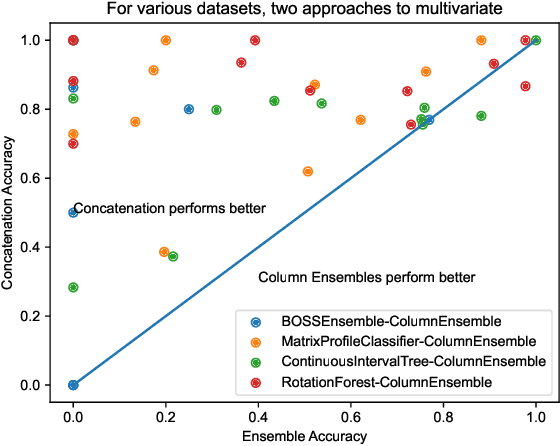
Multivariate time series data are ubiquitous in the application of machine learning to problems in the physical sciences. Chemiresistive sensor arrays are highly promising in chemical detection tasks relevant to industrial, safety, and military applications. Sensor arrays are an inherently multivariate time series data collection tool which demand rapid and accurate classification of arbitrary chemical analytes. Previous research has benchmarked data-agnostic multivariate time series classifiers across diverse multivariate time series supervised tasks in order to find general-purpose classification algorithms. To our knowledge, there has yet to be an effort to survey machine learning and time series classification approaches to chemiresistive hardware sensor arrays for the detection of chemical analytes. In addition to benchmarking existing approaches to multivariate time series classifiers, we incorporate findings from a model survey to propose the novel \textit{ChemTime} approach to sensor array classification for chemical sensing. We design experiments addressing the unique challenges of hardware sensor arrays classification including the rapid classification ability of classifiers and minimization of inference time while maintaining performance for deployed lightweight hardware sensing devices. We find that \textit{ChemTime} is uniquely positioned for the chemical sensing task by combining rapid and early classification of time series with beneficial inference and high accuracy.

ChemVise: Maximizing Out-of-Distribution Chemical Detection with the Novel Application of Zero-Shot Learning

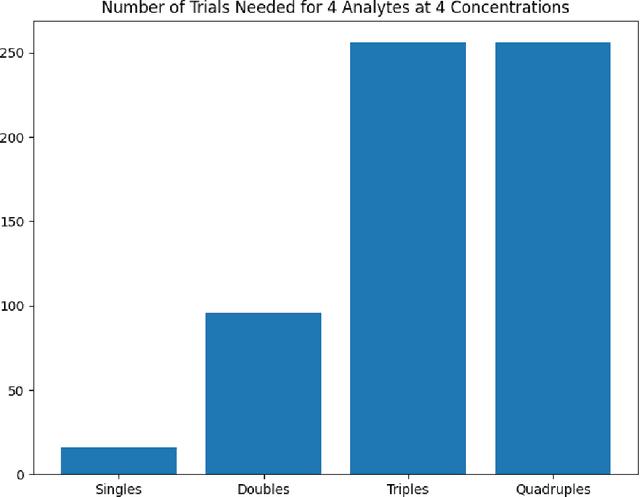
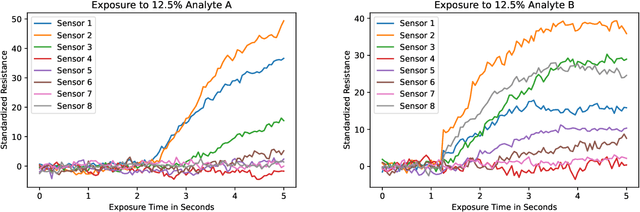
Accurate chemical sensors are vital in medical, military, and home safety applications. Training machine learning models to be accurate on real world chemical sensor data requires performing many diverse, costly experiments in controlled laboratory settings to create a data set. In practice even expensive, large data sets may be insufficient for generalization of a trained model to a real-world testing distribution. Rather than perform greater numbers of experiments requiring exhaustive mixtures of chemical analytes, this research proposes learning approximations of complex exposures from training sets of simple ones by using single-analyte exposure signals as building blocks of a multiple-analyte space. We demonstrate this approach to synthetic sensor responses surprisingly improves the detection of out-of-distribution obscured chemical analytes. Further, we pair these synthetic signals to targets in an information-dense representation space utilizing a large corpus of chemistry knowledge. Through utilization of a semantically meaningful analyte representation spaces along with synthetic targets we achieve rapid analyte classification in the presence of obscurants without corresponding obscured-analyte training data. Transfer learning for supervised learning with molecular representations makes assumptions about the input data. Instead, we borrow from the natural language and natural image processing literature for a novel approach to chemical sensor signal classification using molecular semantics for arbitrary chemical sensor hardware designs.

The Pseudo Projection Operator: Applications of Deep Learning to Projection Based Filtering in Non-Trivial Frequency Regimes

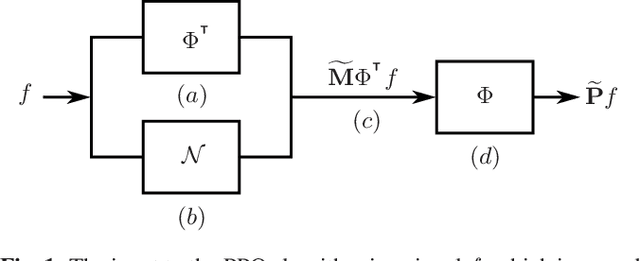
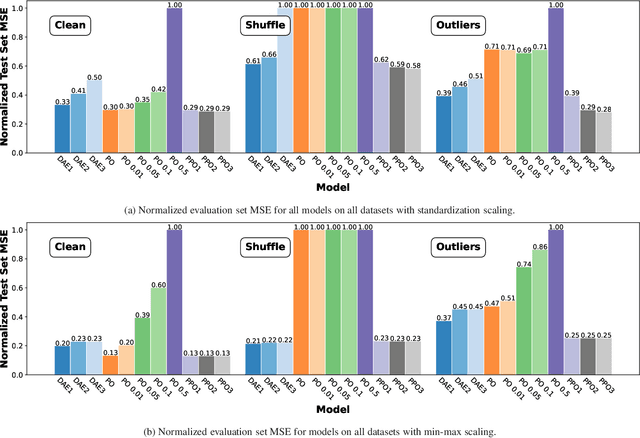
Traditional frequency based projection filters, or projection operators (PO), separate signal and noise through a series of transformations which remove frequencies where noise is present. However, this technique relies on a priori knowledge of what frequencies contain signal and noise and that these frequencies do not overlap, which is difficult to achieve in practice. To address these issues, we introduce a PO-neural network hybrid model, the Pseudo Projection Operator (PPO), which leverages a neural network to perform frequency selection. We compare the filtering capabilities of a PPO, PO, and denoising autoencoder (DAE) on the University of Rochester Multi-Modal Music Performance Dataset with a variety of added noise types. In the majority of experiments, the PPO outperforms both the PO and DAE. Based upon these results, we suggest future application of the PPO to filtering problems in the physical and biological sciences.

Neural Network Ensembles: Theory, Training, and the Importance of Explicit Diversity

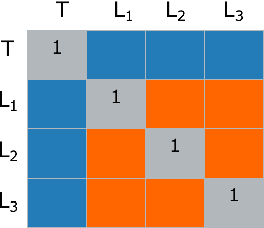
Ensemble learning is a process by which multiple base learners are strategically generated and combined into one composite learner. There are two features that are essential to an ensemble's performance, the individual accuracies of the component learners and the overall diversity in the ensemble. The right balance of learner accuracy and ensemble diversity can improve the performance of machine learning tasks on benchmark and real-world data sets, and recent theoretical and practical work has demonstrated the subtle trade-off between accuracy and diversity in an ensemble. In this paper, we extend the extant literature by providing a deeper theoretical understanding for assessing and improving the optimality of any given ensemble, including random forests and deep neural network ensembles. We also propose a training algorithm for neural network ensembles and demonstrate that our approach provides improved performance when compared to both state-of-the-art individual learners and ensembles of state-of-the-art learners trained using standard loss functions. Our key insight is that it is better to explicitly encourage diversity in an ensemble, rather than merely allowing diversity to occur by happenstance, and that rigorous theoretical bounds on the trade-off between diversity and learner accuracy allow one to know when an optimal arrangement has been achieved.

Anomaly Detection via Graphical Lasso

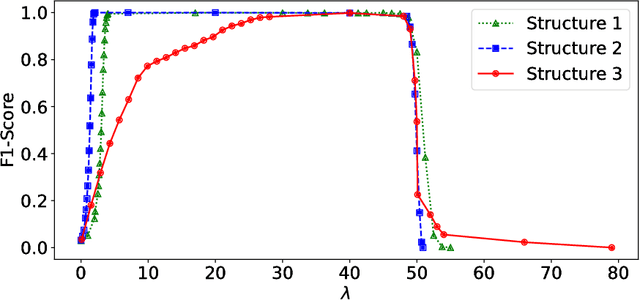
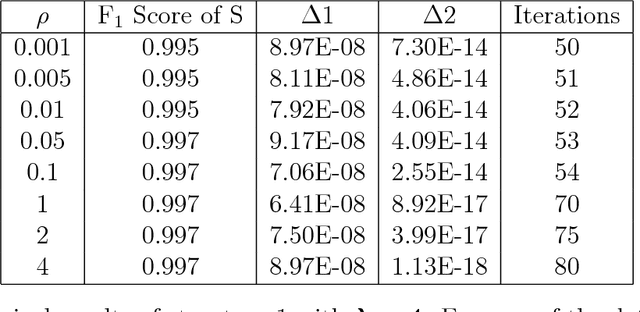
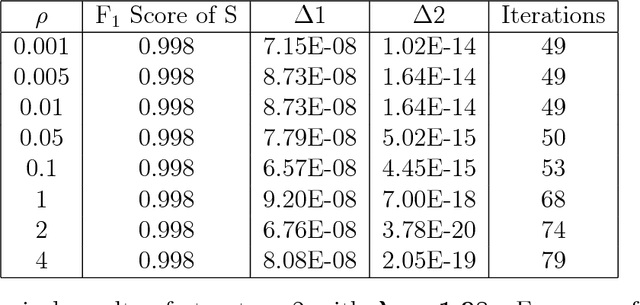
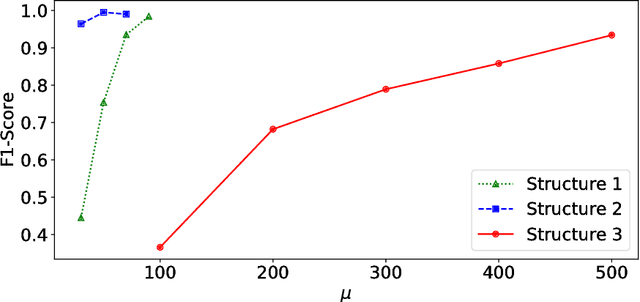
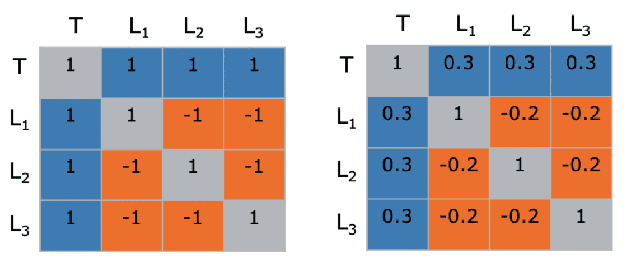
Anomalies and outliers are common in real-world data, and they can arise from many sources, such as sensor faults. Accordingly, anomaly detection is important both for analyzing the anomalies themselves and for cleaning the data for further analysis of its ambient structure. Nonetheless, a precise definition of anomalies is important for automated detection and herein we approach such problems from the perspective of detecting sparse latent effects embedded in large collections of noisy data. Standard Graphical Lasso-based techniques can identify the conditional dependency structure of a collection of random variables based on their sample covariance matrix. However, classic Graphical Lasso is sensitive to outliers in the sample covariance matrix. In particular, several outliers in a sample covariance matrix can destroy the sparsity of its inverse. Accordingly, we propose a novel optimization problem that is similar in spirit to Robust Principal Component Analysis (RPCA) and splits the sample covariance matrix $M$ into two parts, $M=F+S$, where $F$ is the cleaned sample covariance whose inverse is sparse and computable by Graphical Lasso, and $S$ contains the outliers in $M$. We accomplish this decomposition by adding an additional $ \ell_1$ penalty to classic Graphical Lasso, and name it "Robust Graphical Lasso (Rglasso)". Moreover, we propose an Alternating Direction Method of Multipliers (ADMM) solution to the optimization problem which scales to large numbers of unknowns. We evaluate our algorithm on both real and synthetic datasets, obtaining interpretable results and outperforming the standard robust Minimum Covariance Determinant (MCD) method and Robust Principal Component Analysis (RPCA) regarding both accuracy and speed.