Data Quality Measures and Efficient Evaluation Algorithms for Large-Scale High-Dimensional Data

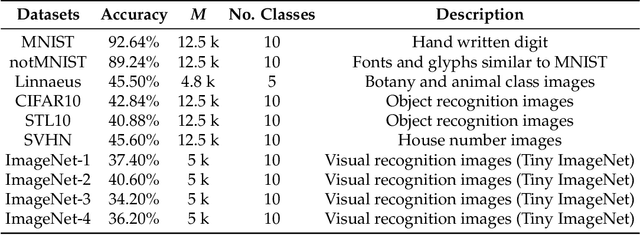
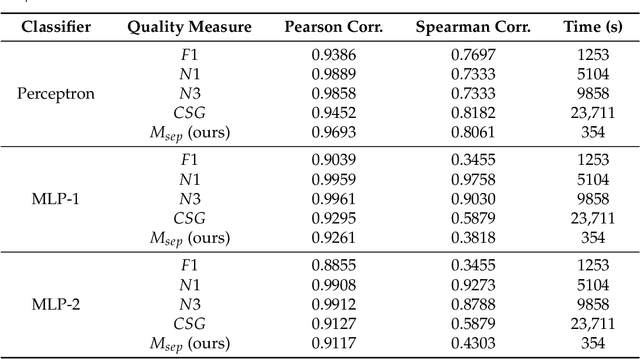
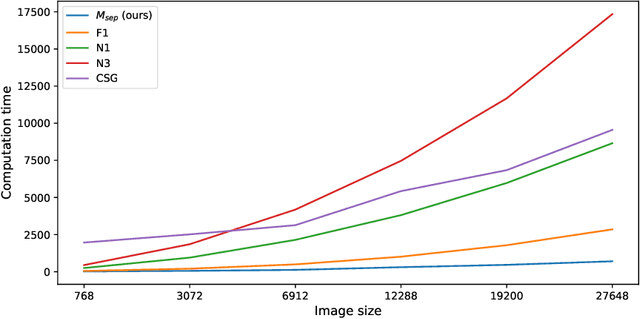
Machine learning has been proven to be effective in various application areas, such as object and speech recognition on mobile systems. Since a critical key to machine learning success is the availability of large training data, many datasets are being disclosed and published online. From a data consumer or manager point of view, measuring data quality is an important first step in the learning process. We need to determine which datasets to use, update, and maintain. However, not many practical ways to measure data quality are available today, especially when it comes to large-scale high-dimensional data, such as images and videos. This paper proposes two data quality measures that can compute class separability and in-class variability, the two important aspects of data quality, for a given dataset. Classical data quality measures tend to focus only on class separability; however, we suggest that in-class variability is another important data quality factor. We provide efficient algorithms to compute our quality measures based on random projections and bootstrapping with statistical benefits on large-scale high-dimensional data. In experiments, we show that our measures are compatible with classical measures on small-scale data and can be computed much more efficiently on large-scale high-dimensional datasets.

Structure Learning of Gaussian Markov Random Fields with False Discovery Rate Control

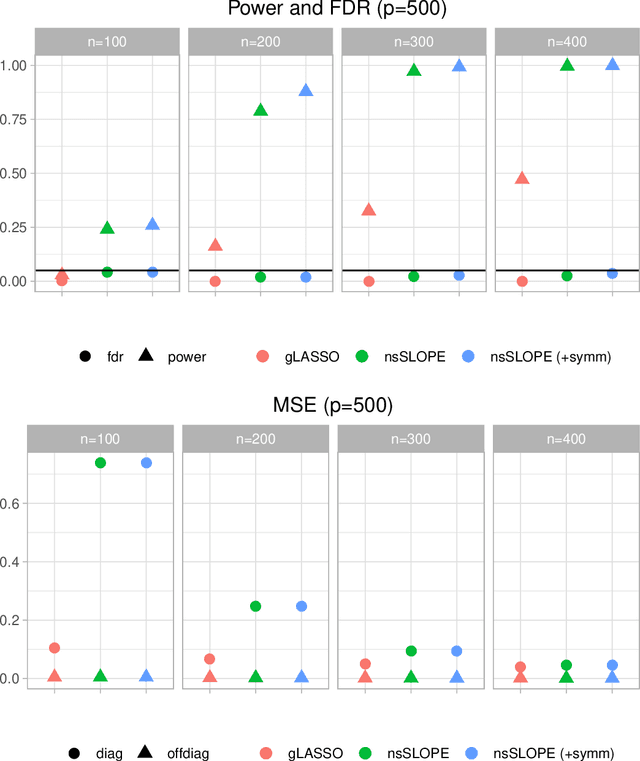
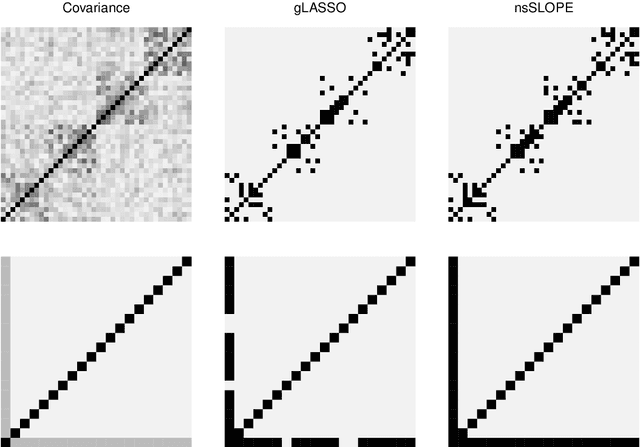
In this paper, we propose a new estimation procedure for discovering the structure of Gaussian Markov random fields (MRFs) with false discovery rate (FDR) control, making use of the sorted l1-norm (SL1) regularization. A Gaussian MRF is an acyclic graph representing a multivariate Gaussian distribution, where nodes are random variables and edges represent the conditional dependence between the connected nodes. Since it is possible to learn the edge structure of Gaussian MRFs directly from data, Gaussian MRFs provide an excellent way to understand complex data by revealing the dependence structure among many inputs features, such as genes, sensors, users, documents, etc. In learning the graphical structure of Gaussian MRFs, it is desired to discover the actual edges of the underlying but unknown probabilistic graphical model-it becomes more complicated when the number of random variables (features) p increases, compared to the number of data points n. In particular, when p >> n, it is statistically unavoidable for any estimation procedure to include false edges. Therefore, there have been many trials to reduce the false detection of edges, in particular, using different types of regularization on the learning parameters. Our method makes use of the SL1 regularization, introduced recently for model selection in linear regression. We focus on the benefit of SL1 regularization that it can be used to control the FDR of detecting important random variables. Adapting SL1 for probabilistic graphical models, we show that SL1 can be used for the structure learning of Gaussian MRFs using our suggested procedure nsSLOPE (neighborhood selection Sorted L-One Penalized Estimation), controlling the FDR of detecting edges.

Compressed Learning of Deep Neural Networks for OpenCL-Capable Embedded Systems

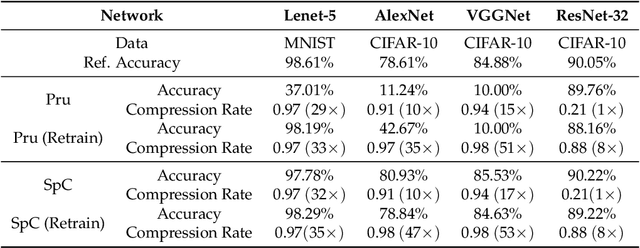
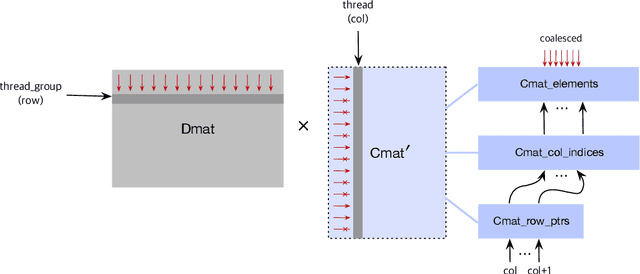
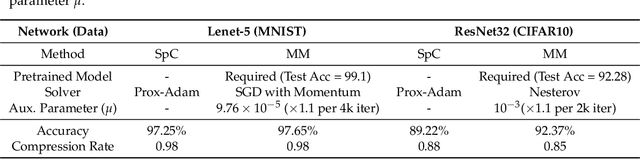
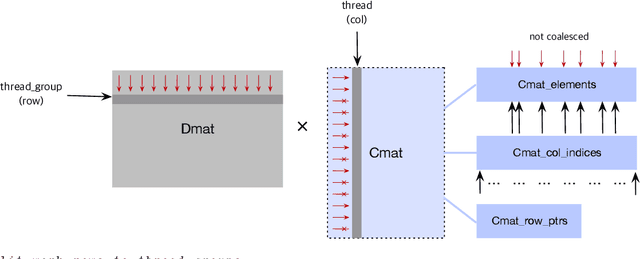
Deep neural networks (DNNs) have been quite successful in solving many complex learning problems. However, DNNs tend to have a large number of learning parameters, leading to a large memory and computation requirement. In this paper, we propose a model compression framework for efficient training and inference of deep neural networks on embedded systems. Our framework provides data structures and kernels for OpenCL-based parallel forward and backward computation in a compressed form. In particular, our method learns sparse representations of parameters using $\ell_1$-based sparse coding while training, storing them in compressed sparse matrices. Unlike the previous works, our method does not require a pre-trained model as an input and therefore can be more versatile for different application environments. Even though the use of $\ell_1$-based sparse coding for model compression is not new, we show that it can be far more effective than previously reported when we use proximal point algorithms and the technique of debiasing. Our experiments show that our method can produce minimal learning models suitable for small embedded devices.

Fast Saddle-Point Algorithm for Generalized Dantzig Selector and FDR Control with the Ordered l1-Norm

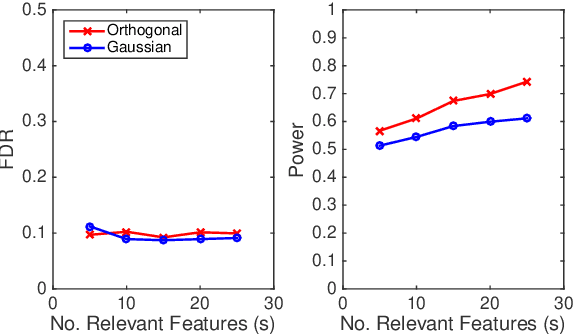
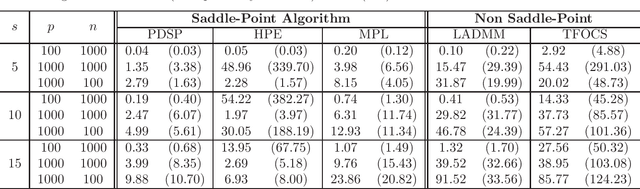
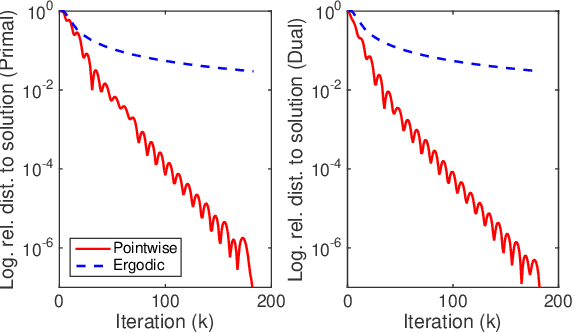
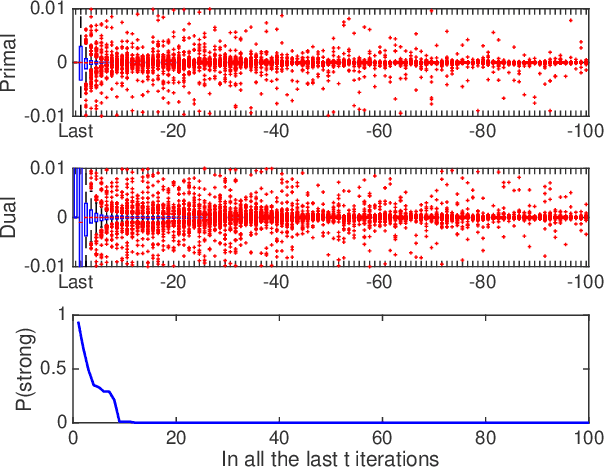
In this paper we propose a primal-dual proximal extragradient algorithm to solve the generalized Dantzig selector (GDS) estimation problem, based on a new convex-concave saddle-point (SP) reformulation. Our new formulation makes it possible to adopt recent developments in saddle-point optimization, to achieve the optimal $O(1/k)$ rate of convergence. Compared to the optimal non-SP algorithms, ours do not require specification of sensitive parameters that affect algorithm performance or solution quality. We also provide a new analysis showing a possibility of local acceleration to achieve the rate of $O(1/k^2)$ in special cases even without strong convexity or strong smoothness. As an application, we propose a GDS equipped with the ordered $\ell_1$-norm, showing its false discovery rate control properties in variable selection. Algorithm performance is compared between ours and other alternatives, including the linearized ADMM, Nesterov's smoothing, Nemirovski's mirror-prox, and the accelerated hybrid proximal extragradient techniques.

Approximate Stochastic Subgradient Estimation Training for Support Vector Machines

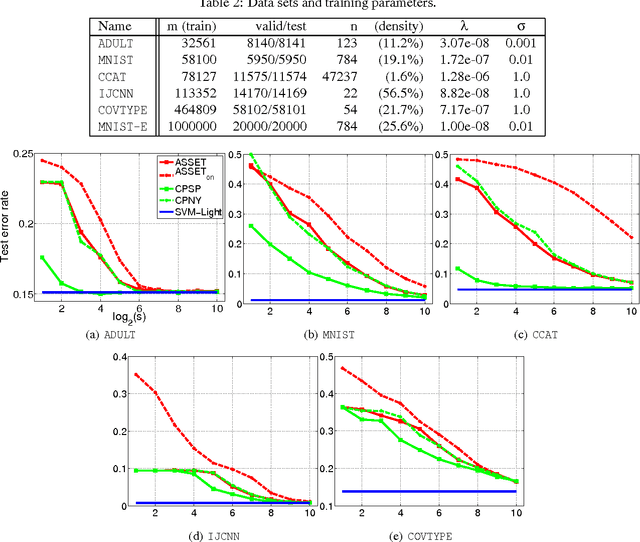
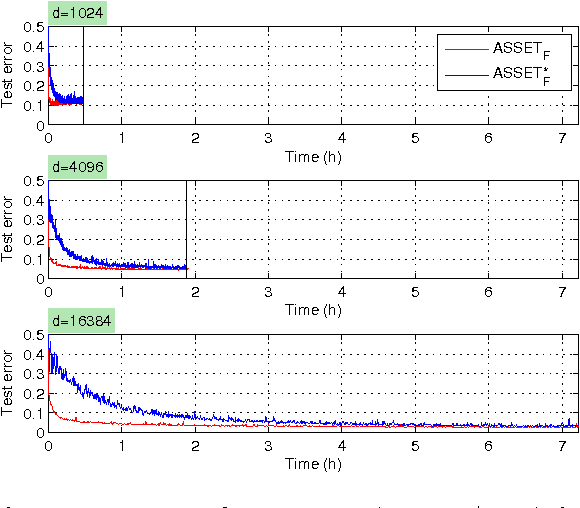
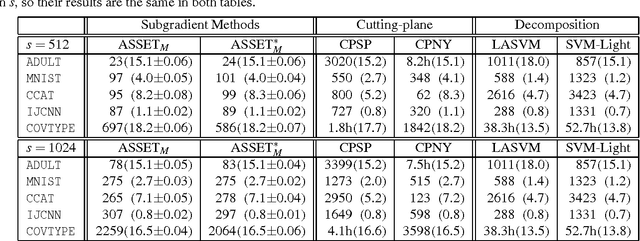
Subgradient algorithms for training support vector machines have been quite successful for solving large-scale and online learning problems. However, they have been restricted to linear kernels and strongly convex formulations. This paper describes efficient subgradient approaches without such limitations. Our approaches make use of randomized low-dimensional approximations to nonlinear kernels, and minimization of a reduced primal formulation using an algorithm based on robust stochastic approximation, which do not require strong convexity. Experiments illustrate that our approaches produce solutions of comparable prediction accuracy with the solutions acquired from existing SVM solvers, but often in much shorter time. We also suggest efficient prediction schemes that depend only on the dimension of kernel approximation, not on the number of support vectors.