Approximate Stochastic Subgradient Estimation Training for Support Vector Machines
Paper and Code
Nov 03, 2011
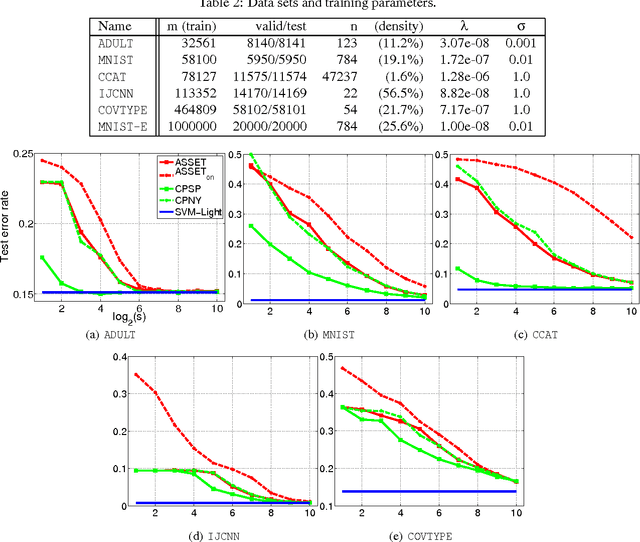
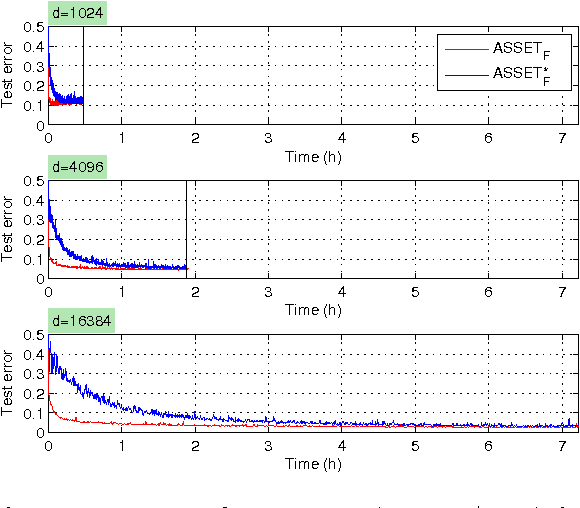
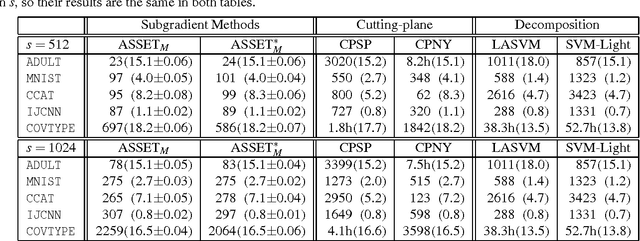
Subgradient algorithms for training support vector machines have been quite successful for solving large-scale and online learning problems. However, they have been restricted to linear kernels and strongly convex formulations. This paper describes efficient subgradient approaches without such limitations. Our approaches make use of randomized low-dimensional approximations to nonlinear kernels, and minimization of a reduced primal formulation using an algorithm based on robust stochastic approximation, which do not require strong convexity. Experiments illustrate that our approaches produce solutions of comparable prediction accuracy with the solutions acquired from existing SVM solvers, but often in much shorter time. We also suggest efficient prediction schemes that depend only on the dimension of kernel approximation, not on the number of support vectors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge