Uncertainty Quantification over Graph with Conformalized Graph Neural Networks

Graph Neural Networks (GNNs) are powerful machine learning prediction models on graph-structured data. However, GNNs lack rigorous uncertainty estimates, limiting their reliable deployment in settings where the cost of errors is significant. We propose conformalized GNN (CF-GNN), extending conformal prediction (CP) to graph-based models for guaranteed uncertainty estimates. Given an entity in the graph, CF-GNN produces a prediction set/interval that provably contains the true label with pre-defined coverage probability (e.g. 90%). We establish a permutation invariance condition that enables the validity of CP on graph data and provide an exact characterization of the test-time coverage. Moreover, besides valid coverage, it is crucial to reduce the prediction set size/interval length for practical use. We observe a key connection between non-conformity scores and network structures, which motivates us to develop a topology-aware output correction model that learns to update the prediction and produces more efficient prediction sets/intervals. Extensive experiments show that CF-GNN achieves any pre-defined target marginal coverage while significantly reducing the prediction set/interval size by up to 74% over the baselines. It also empirically achieves satisfactory conditional coverage over various raw and network features.

The Projected Power Method: An Efficient Algorithm for Joint Alignment from Pairwise Differences

Various applications involve assigning discrete label values to a collection of objects based on some pairwise noisy data. Due to the discrete---and hence nonconvex---structure of the problem, computing the optimal assignment (e.g.~maximum likelihood assignment) becomes intractable at first sight. This paper makes progress towards efficient computation by focusing on a concrete joint alignment problem---that is, the problem of recovering $n$ discrete variables $x_i \in \{1,\cdots, m\}$, $1\leq i\leq n$ given noisy observations of their modulo differences $\{x_i - x_j~\mathsf{mod}~m\}$. We propose a low-complexity and model-free procedure, which operates in a lifted space by representing distinct label values in orthogonal directions, and which attempts to optimize quadratic functions over hypercubes. Starting with a first guess computed via a spectral method, the algorithm successively refines the iterates via projected power iterations. We prove that for a broad class of statistical models, the proposed projected power method makes no error---and hence converges to the maximum likelihood estimate---in a suitable regime. Numerical experiments have been carried out on both synthetic and real data to demonstrate the practicality of our algorithm. We expect this algorithmic framework to be effective for a broad range of discrete assignment problems.

False Discoveries Occur Early on the Lasso Path

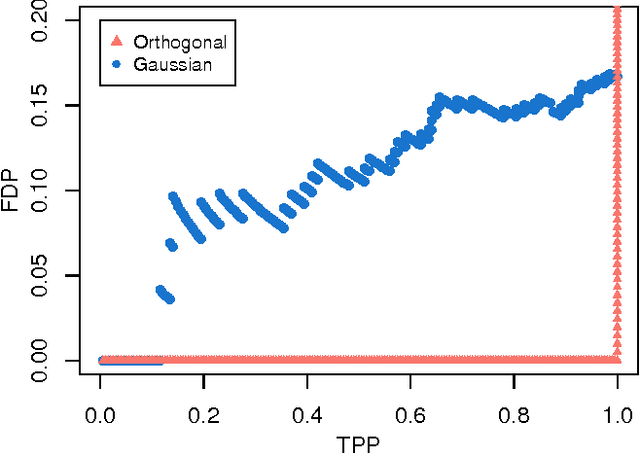
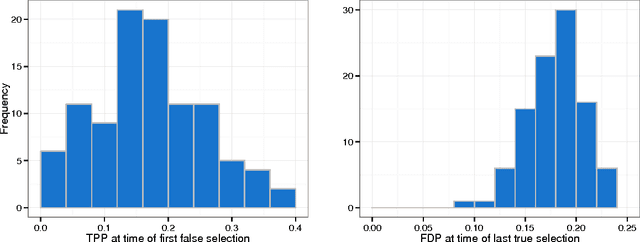
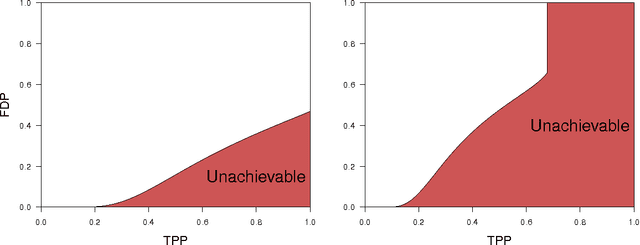
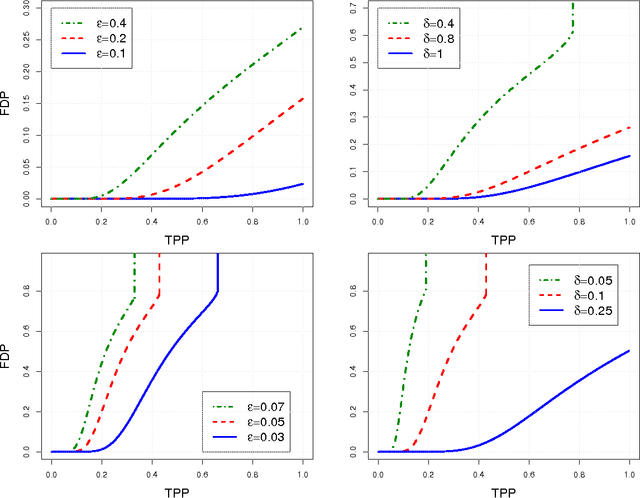
In regression settings where explanatory variables have very low correlations and there are relatively few effects, each of large magnitude, we expect the Lasso to find the important variables with few errors, if any. This paper shows that in a regime of linear sparsity---meaning that the fraction of variables with a non-vanishing effect tends to a constant, however small---this cannot really be the case, even when the design variables are stochastically independent. We demonstrate that true features and null features are always interspersed on the Lasso path, and that this phenomenon occurs no matter how strong the effect sizes are. We derive a sharp asymptotic trade-off between false and true positive rates or, equivalently, between measures of type I and type II errors along the Lasso path. This trade-off states that if we ever want to achieve a type II error (false negative rate) under a critical value, then anywhere on the Lasso path the type I error (false positive rate) will need to exceed a given threshold so that we can never have both errors at a low level at the same time. Our analysis uses tools from approximate message passing (AMP) theory as well as novel elements to deal with a possibly adaptive selection of the Lasso regularizing parameter.