Statistical signatures of abstraction in deep neural networks

We study how abstract representations emerge in a Deep Belief Network (DBN) trained on benchmark datasets. Our analysis targets the principles of learning in the early stages of information processing, starting from the "primordial soup" of the under-sampling regime. As the data is processed by deeper and deeper layers, features are detected and removed, transferring more and more "context-invariant" information to deeper layers. We show that the representation approaches an universal model -- the Hierarchical Feature Model (HFM) -- determined by the principle of maximal relevance. Relevance quantifies the uncertainty on the model of the data, thus suggesting that "meaning" -- i.e. syntactic information -- is that part of the data which is not yet captured by a model. Our analysis shows that shallow layers are well described by pairwise Ising models, which provide a representation of the data in terms of generic, low order features. We also show that plasticity increases with depth, in a similar way as it does in the brain. These findings suggest that DBNs are capable of extracting a hierarchy of features from the data which is consistent with the principle of maximal relevance.

Multiscale Relevance of Natural Images

We use an agnostic information-theoretic approach to investigate the statistical properties of natural images. We introduce the Multiscale Relevance (MSR) measure to assess the robustness of images to compression at all scales. Starting in a controlled environment, we characterize the MSR of synthetic random textures as function of image roughness H and other relevant parameters. We then extend the analysis to natural images and find striking similarities with critical (H = 0) random textures. We show that the MSR is more robust and informative of image content than classical methods such as power spectrum analysis. Finally, we confront the MSR to classical measures for the calibration of common procedures such as color mapping and denoising. Overall, the MSR approach appears to be a good candidate for advanced image analysis and image processing, while providing a good level of physical interpretability.

Occam learning

We discuss probabilistic neural network models for unsupervised learning where the distribution of the hidden layer is fixed. We argue that learning machines with this architecture enjoy a number of desirable properties. For example, the model can be chosen as a simple and interpretable one, it does not need to be over-parametrised and training is argued to be efficient in a thermodynamic sense. When hidden units are binary variables, these models have a natural interpretation in terms of features. We show that the featureless state corresponds to a state of maximal ignorance about the features and that learning the first feature depends on non-Gaussian statistical properties of the data. We suggest that the distribution of hidden variables should be chosen according to the principle of maximal relevance. We introduce the Hierarchical Feature Model as an example of a model that satisfies this principle, and that encodes an a priori organisation of the feature space. We present extensive numerical experiments in order i) to test that the internal representation of learning machines can indeed be independent of the data with which they are trained and ii) that only a finite number of features are needed to describe a datasets.

Quantifying Relevance in Learning and Inference

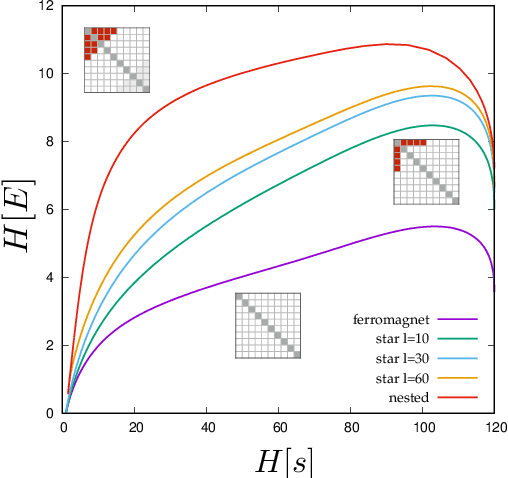
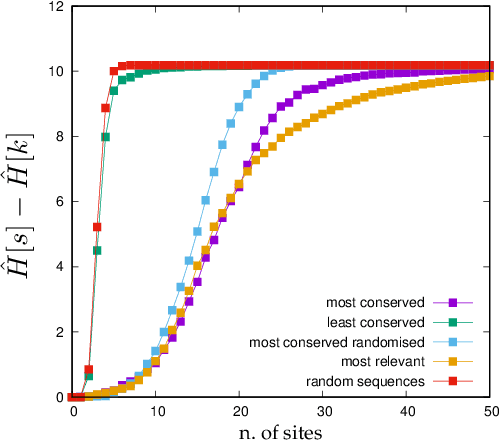
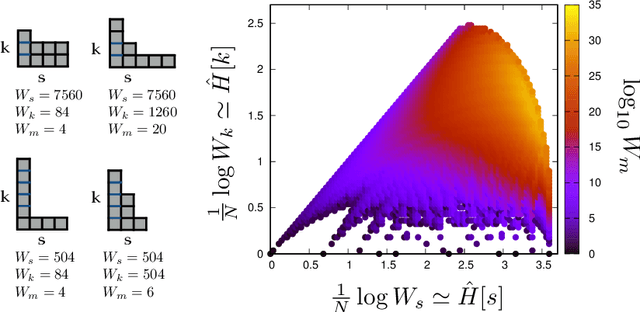
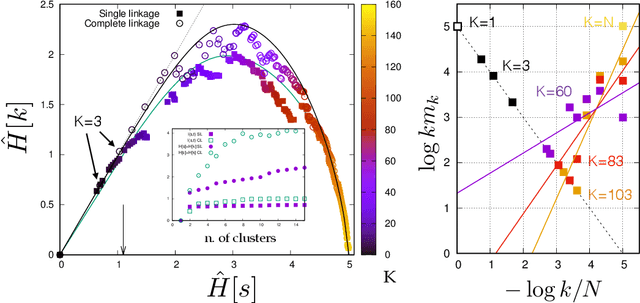
Learning is a distinctive feature of intelligent behaviour. High-throughput experimental data and Big Data promise to open new windows on complex systems such as cells, the brain or our societies. Yet, the puzzling success of Artificial Intelligence and Machine Learning shows that we still have a poor conceptual understanding of learning. These applications push statistical inference into uncharted territories where data is high-dimensional and scarce, and prior information on "true" models is scant if not totally absent. Here we review recent progress on understanding learning, based on the notion of "relevance". The relevance, as we define it here, quantifies the amount of information that a dataset or the internal representation of a learning machine contains on the generative model of the data. This allows us to define maximally informative samples, on one hand, and optimal learning machines on the other. These are ideal limits of samples and of machines, that contain the maximal amount of information about the unknown generative process, at a given resolution (or level of compression). Both ideal limits exhibit critical features in the statistical sense: Maximally informative samples are characterised by a power-law frequency distribution (statistical criticality) and optimal learning machines by an anomalously large susceptibility. The trade-off between resolution (i.e. compression) and relevance distinguishes the regime of noisy representations from that of lossy compression. These are separated by a special point characterised by Zipf's law statistics. This identifies samples obeying Zipf's law as the most compressed loss-less representations that are optimal in the sense of maximal relevance. Criticality in optimal learning machines manifests in an exponential degeneracy of energy levels, that leads to unusual thermodynamic properties.

A random energy approach to deep learning

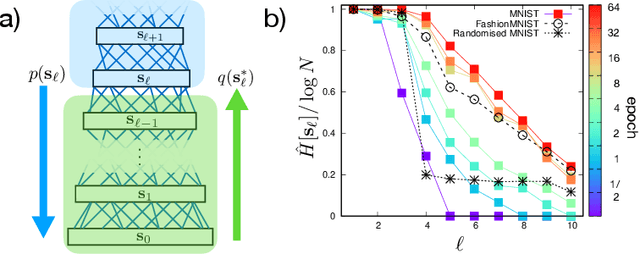
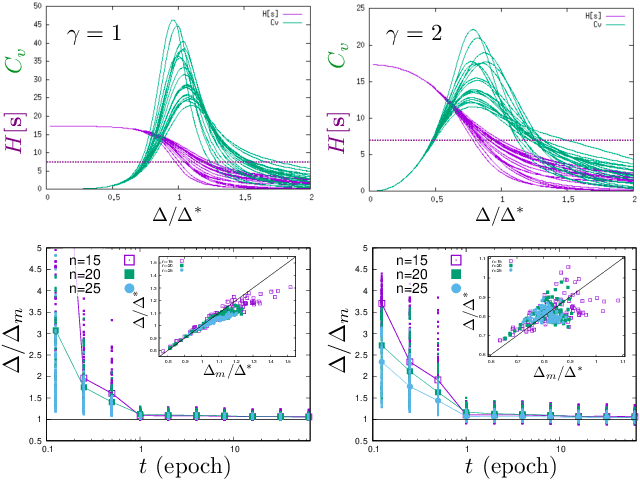
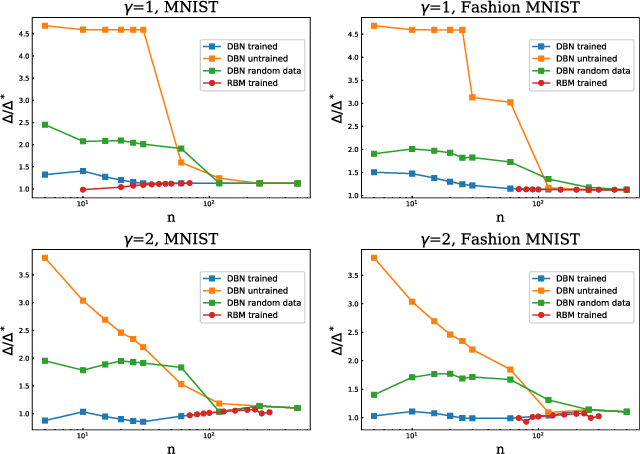
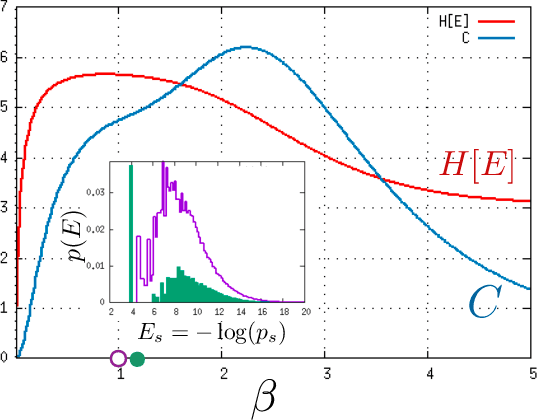
We study a generic ensemble of deep belief networks which is parametrized by the distribution of energy levels of the hidden states of each layer. We show that, within a random energy approach, statistical dependence can propagate from the visible to deep layers only if each layer is tuned close to the critical point during learning. As a consequence, efficiently trained learning machines are characterised by a broad distribution of energy levels. The analysis of Deep Belief Networks and Restricted Boltzmann Machines on different datasets confirms these conclusions.

Statistical Inference of Minimally Complex Models

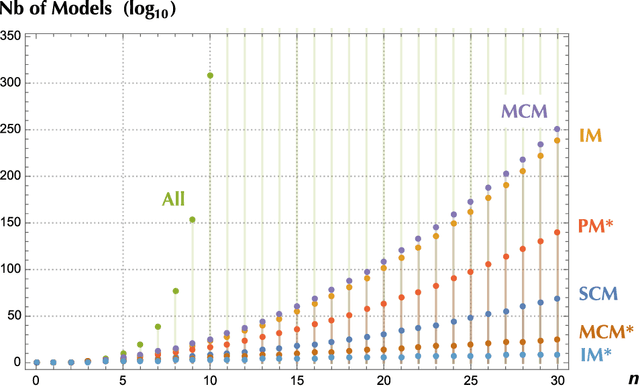
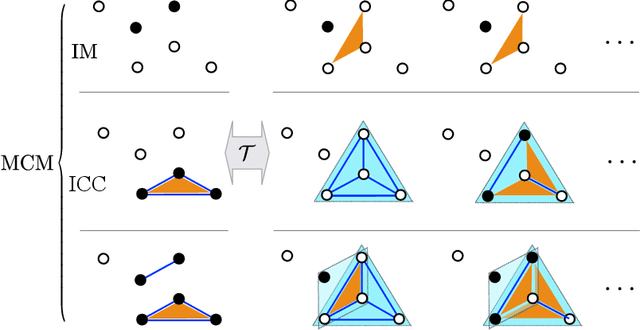
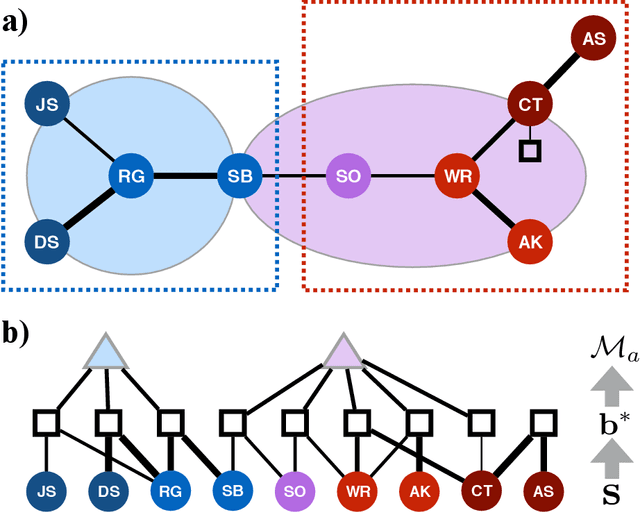
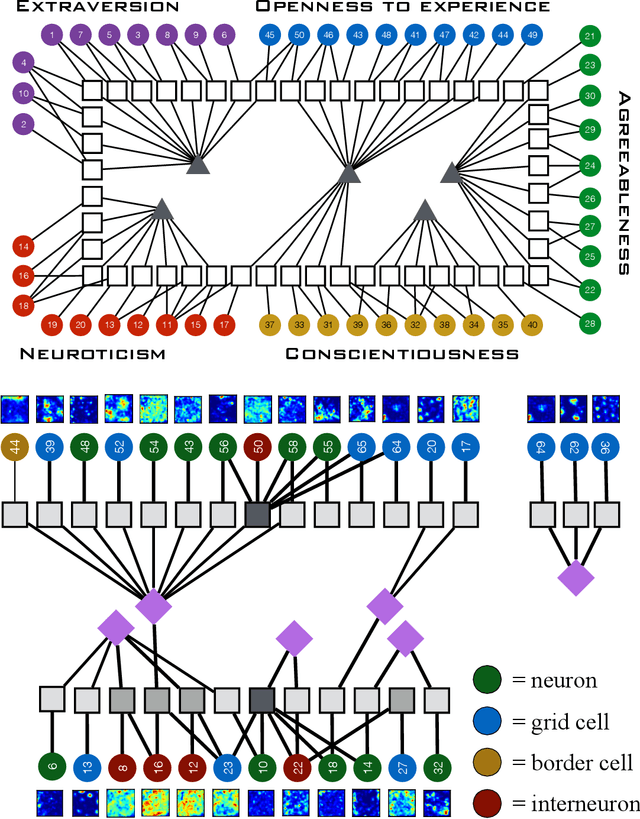
Finding the best model that describes a high dimensional dataset, is a daunting task. For binary data, we show that this becomes feasible, if the search is restricted to simple models. These models -- that we call Minimally Complex Models (MCMs) -- are simple because they are composed of independent components of minimal complexity, in terms of description length. Simple models are easy to infer and to sample from. In addition, model selection within the MCMs' class is invariant with respect to changes in the representation of the data. They portray the structure of dependencies among variables in a simple way. They provide robust predictions on dependencies and symmetries, as illustrated in several examples. MCMs may contain interactions between variables of any order. So, for example, our approach reveals whether a dataset is appropriately described by a pairwise interaction model.

On the complexity of logistic regression models

We investigate the complexity of logistic regression models which is defined by counting the number of indistinguishable distributions that the model can represent (Balasubramanian, 1997). We find that the complexity of logistic models with binary inputs does not only depend on the number of parameters but also on the distribution of inputs in a non-trivial way which standard treatments of complexity do not address. In particular, we observe that correlations among inputs induce effective dependencies among parameters thus constraining the model and, consequently, reducing its complexity. We derive simple relations for the upper and lower bounds of the complexity. Furthermore, we show analytically that, defining the model parameters on a finite support rather than the entire axis, decreases the complexity in a manner that critically depends on the size of the domain. Based on our findings, we propose a novel model selection criterion which takes into account the entropy of the input distribution. We test our proposal on the problem of selecting the input variables of a logistic regression model in a Bayesian Model Selection framework. In our numerical tests, we find that, while the reconstruction errors of standard model selection approaches (AIC, BIC, $\ell_1$ regularization) strongly depend on the sparsity of the ground truth, the reconstruction error of our method is always close to the minimum in all conditions of sparsity, data size and strength of input correlations. Finally, we observe that, when considering categorical instead of binary inputs, in a simple and mathematically tractable case, the contribution of the alphabet size to the complexity is very small compared to that of parameter space dimension. We further explore the issue by analysing the dataset of the "13 keys to the White House" which is a method for forecasting the outcomes of US presidential elections.

The Stochastic complexity of spin models: Are pairwise models really simple?

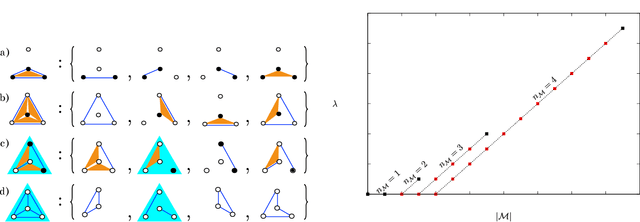
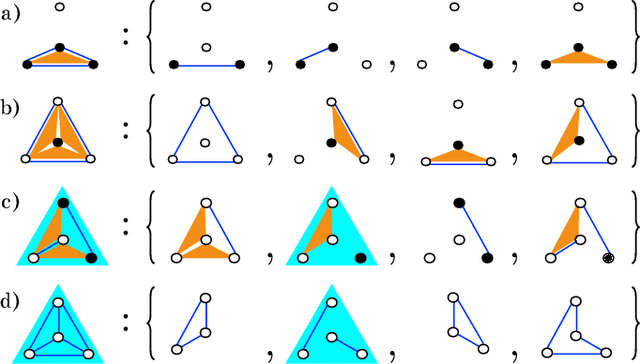
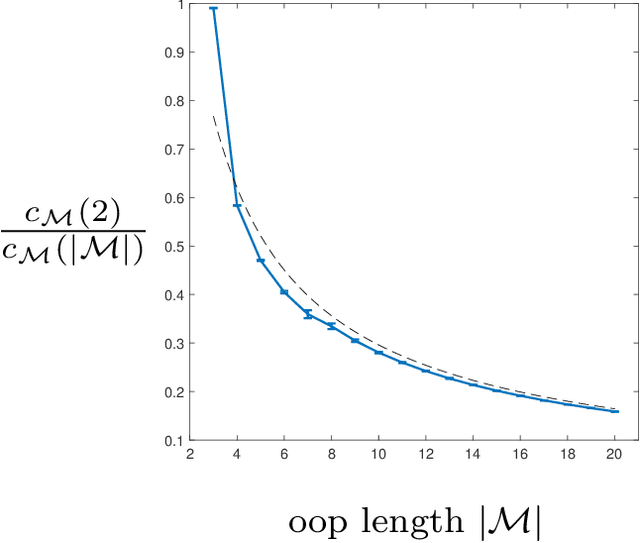
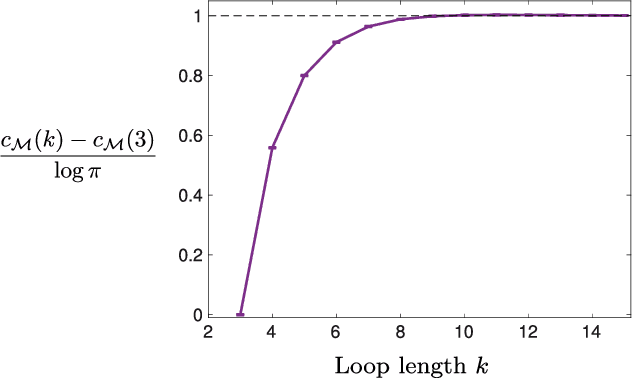
Models can be simple for different reasons: because they yield a simple and computationally efficient interpretation of a generic dataset (e.g. in terms of pairwise dependences) - as in statistical learning - or because they capture the essential ingredients of a specific phenomenon - as e.g. in physics - leading to non-trivial falsifiable predictions. In information theory and Bayesian inference, the simplicity of a model is precisely quantified in the stochastic complexity, which measures the number of bits needed to encode its parameters. In order to understand how simple models look like, we study the stochastic complexity of spin models with interactions of arbitrary order. We highlight the existence of invariances with respect to bijections within the space of operators, which allow us to partition the space of all models into equivalence classes, in which models share the same complexity. We thus found that the complexity (or simplicity) of a model is not determined by the order of the interactions, but rather by their mutual arrangements. Models where statistical dependencies are localized on non-overlapping groups of few variables (and that afford predictions on independencies that are easy to falsify) are simple. On the contrary, fully connected pairwise models, which are often used in statistical learning, appear to be highly complex, because of their extended set of interactions.

Resolution and Relevance Trade-offs in Deep Learning

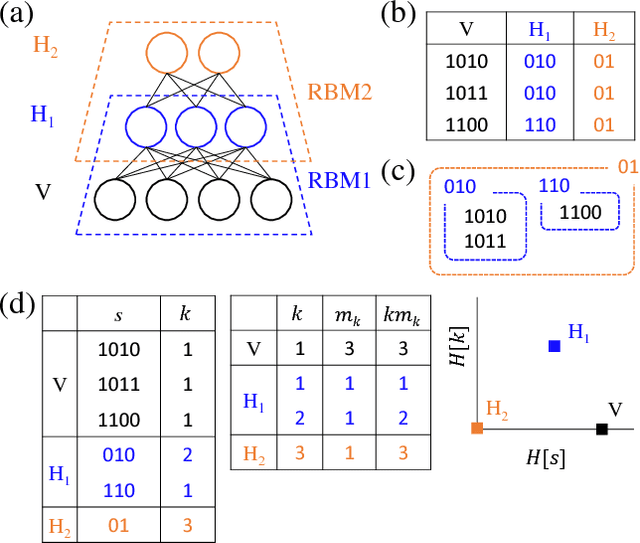
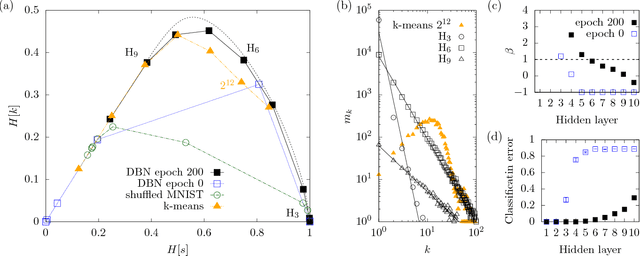
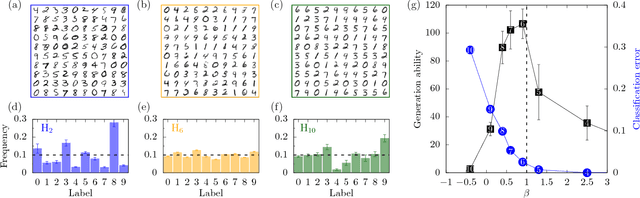
Deep learning has been successfully applied to various tasks, but its underlying mechanism remains unclear. Neural networks associate similar inputs in the visible layer to the same state of hidden variables in deep layers. The fraction of inputs that are associated to the same state is a natural measure of similarity and is simply related to the cost in bits required to represent these inputs. The degeneracy of states with the same information cost provides instead a natural measure of noise and is simply related the entropy of the frequency of states, that we call relevance. Representations with minimal noise, at a given level of similarity (resolution), are those that maximise the relevance. A signature of such efficient representations is that frequency distributions follow power laws. We show, in extensive numerical experiments, that deep neural networks extract a hierarchy of efficient representations from data, because they i) achieve low levels of noise (i.e. high relevance) and ii) exhibit power law distributions. We also find that the layer that is most efficient to reliably generate patterns of training data is the one for which relevance and resolution are traded at the same price, which implies that frequency distribution follows Zipf's law.

Sparse model selection in the highly under-sampled regime

We propose a method for recovering the structure of a sparse undirected graphical model when very few samples are available. The method decides about the presence or absence of bonds between pairs of variable by considering one pair at a time and using a closed form formula, analytically derived by calculating the posterior probability for every possible model explaining a two body system using Jeffreys prior. The approach does not rely on the optimisation of any cost functions and consequently is much faster than existing algorithms. Despite this time and computational advantage, numerical results show that for several sparse topologies the algorithm is comparable to the best existing algorithms, and is more accurate in the presence of hidden variables. We apply this approach to the analysis of US stock market data and to neural data, in order to show its efficiency in recovering robust statistical dependencies in real data with non stationary correlations in time and space.