Quantifying Relevance in Learning and Inference
Paper and Code
Feb 01, 2022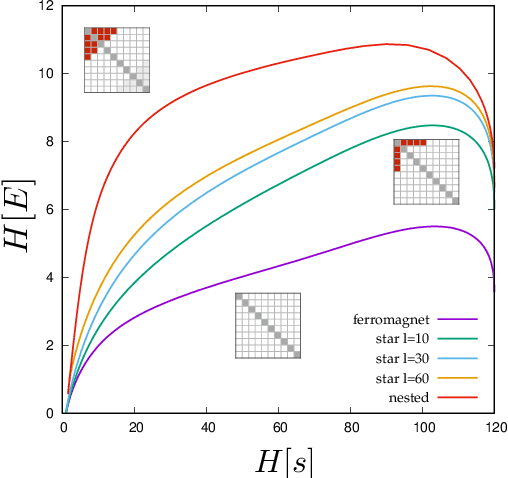
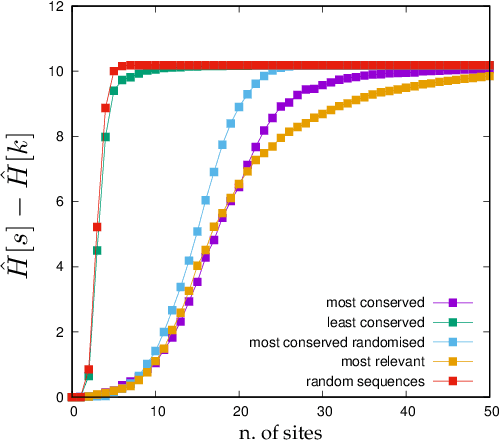
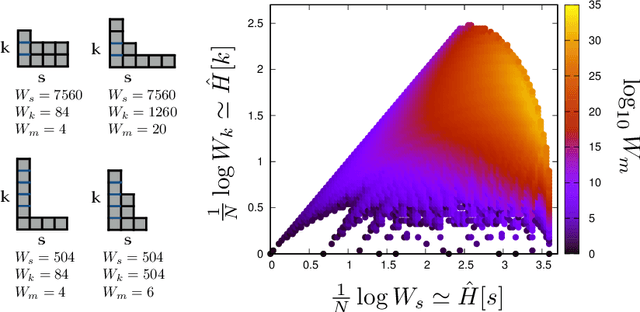
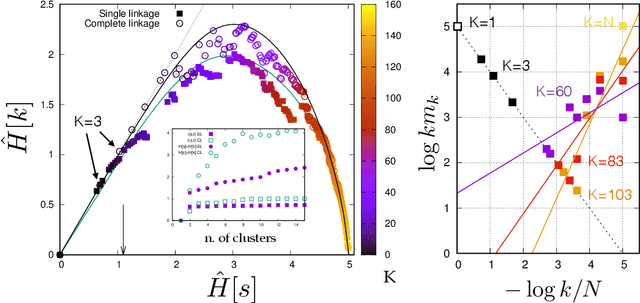
Learning is a distinctive feature of intelligent behaviour. High-throughput experimental data and Big Data promise to open new windows on complex systems such as cells, the brain or our societies. Yet, the puzzling success of Artificial Intelligence and Machine Learning shows that we still have a poor conceptual understanding of learning. These applications push statistical inference into uncharted territories where data is high-dimensional and scarce, and prior information on "true" models is scant if not totally absent. Here we review recent progress on understanding learning, based on the notion of "relevance". The relevance, as we define it here, quantifies the amount of information that a dataset or the internal representation of a learning machine contains on the generative model of the data. This allows us to define maximally informative samples, on one hand, and optimal learning machines on the other. These are ideal limits of samples and of machines, that contain the maximal amount of information about the unknown generative process, at a given resolution (or level of compression). Both ideal limits exhibit critical features in the statistical sense: Maximally informative samples are characterised by a power-law frequency distribution (statistical criticality) and optimal learning machines by an anomalously large susceptibility. The trade-off between resolution (i.e. compression) and relevance distinguishes the regime of noisy representations from that of lossy compression. These are separated by a special point characterised by Zipf's law statistics. This identifies samples obeying Zipf's law as the most compressed loss-less representations that are optimal in the sense of maximal relevance. Criticality in optimal learning machines manifests in an exponential degeneracy of energy levels, that leads to unusual thermodynamic properties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge