Sequential sampling without comparison to boundary through model-free reinforcement learning

Although evidence integration to the boundary model has successfully explained a wide range of behavioral and neural data in decision making under uncertainty, how animals learn and optimize the boundary remains unresolved. Here, we propose a model-free reinforcement learning algorithm for perceptual decisions under uncertainty that dispenses entirely with the concepts of decision boundary and evidence accumulation. Our model learns whether to commit to a decision given the available evidence or continue sampling information at a cost. We reproduced the canonical features of perceptual decision-making such as dependence of accuracy and reaction time on evidence strength, modulation of speed-accuracy trade-off by payoff regime, and many others. By unifying learning and decision making within the same framework, this model can account for unstable behavior during training as well as stabilized post-training behavior, opening the door to revisiting the extensive volumes of discarded training data in the decision science literature.

Quantifying Relevance in Learning and Inference

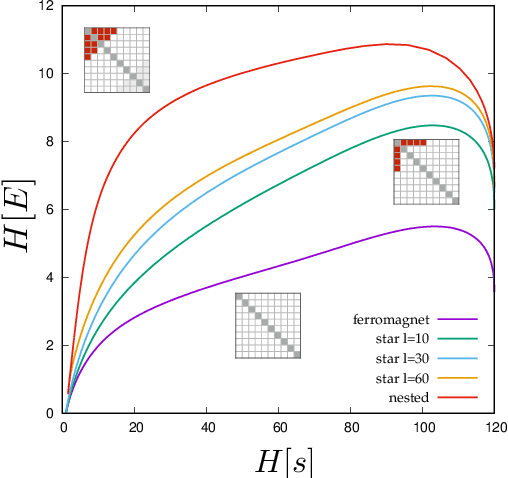
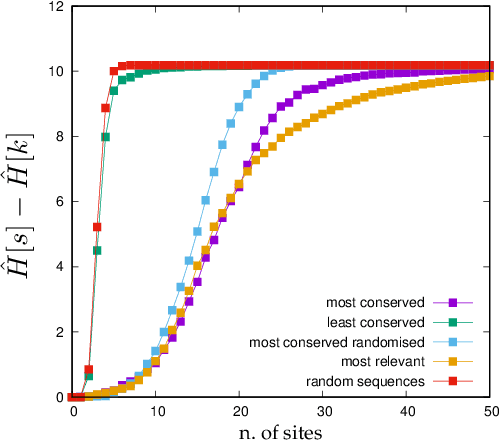
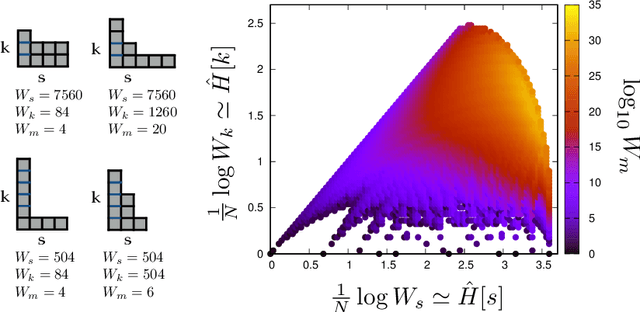
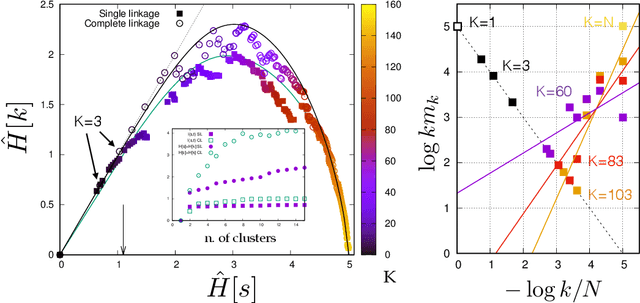
Learning is a distinctive feature of intelligent behaviour. High-throughput experimental data and Big Data promise to open new windows on complex systems such as cells, the brain or our societies. Yet, the puzzling success of Artificial Intelligence and Machine Learning shows that we still have a poor conceptual understanding of learning. These applications push statistical inference into uncharted territories where data is high-dimensional and scarce, and prior information on "true" models is scant if not totally absent. Here we review recent progress on understanding learning, based on the notion of "relevance". The relevance, as we define it here, quantifies the amount of information that a dataset or the internal representation of a learning machine contains on the generative model of the data. This allows us to define maximally informative samples, on one hand, and optimal learning machines on the other. These are ideal limits of samples and of machines, that contain the maximal amount of information about the unknown generative process, at a given resolution (or level of compression). Both ideal limits exhibit critical features in the statistical sense: Maximally informative samples are characterised by a power-law frequency distribution (statistical criticality) and optimal learning machines by an anomalously large susceptibility. The trade-off between resolution (i.e. compression) and relevance distinguishes the regime of noisy representations from that of lossy compression. These are separated by a special point characterised by Zipf's law statistics. This identifies samples obeying Zipf's law as the most compressed loss-less representations that are optimal in the sense of maximal relevance. Criticality in optimal learning machines manifests in an exponential degeneracy of energy levels, that leads to unusual thermodynamic properties.

Restricted Boltzmann Machines as Models of Interacting Variables

We study the type of distributions that Restricted Boltzmann Machines (RBMs) with different activation functions can express by investigating the effect of the activation function of the hidden nodes on the marginal distribution they impose on observed binary nodes. We report an exact expression for these marginals in the form of a model of interacting binary variables with the explicit form of the interactions depending on the hidden node activation function. We study the properties of these interactions in detail and evaluate how the accuracy with which the RBM approximates distributions over binary variables depends on the hidden node activation function and on the number of hidden nodes. When the inferred RBM parameters are weak, an intuitive pattern is found for the expression of the interaction terms which reduces substantially the differences across activation functions. We show that the weak parameter approximation is a good approximation for different RBMs trained on the MNIST dataset. Interestingly, in these cases, the mapping reveals that the inferred models are essentially low order interaction models.

On the complexity of logistic regression models

We investigate the complexity of logistic regression models which is defined by counting the number of indistinguishable distributions that the model can represent (Balasubramanian, 1997). We find that the complexity of logistic models with binary inputs does not only depend on the number of parameters but also on the distribution of inputs in a non-trivial way which standard treatments of complexity do not address. In particular, we observe that correlations among inputs induce effective dependencies among parameters thus constraining the model and, consequently, reducing its complexity. We derive simple relations for the upper and lower bounds of the complexity. Furthermore, we show analytically that, defining the model parameters on a finite support rather than the entire axis, decreases the complexity in a manner that critically depends on the size of the domain. Based on our findings, we propose a novel model selection criterion which takes into account the entropy of the input distribution. We test our proposal on the problem of selecting the input variables of a logistic regression model in a Bayesian Model Selection framework. In our numerical tests, we find that, while the reconstruction errors of standard model selection approaches (AIC, BIC, $\ell_1$ regularization) strongly depend on the sparsity of the ground truth, the reconstruction error of our method is always close to the minimum in all conditions of sparsity, data size and strength of input correlations. Finally, we observe that, when considering categorical instead of binary inputs, in a simple and mathematically tractable case, the contribution of the alphabet size to the complexity is very small compared to that of parameter space dimension. We further explore the issue by analysing the dataset of the "13 keys to the White House" which is a method for forecasting the outcomes of US presidential elections.

Sparse model selection in the highly under-sampled regime

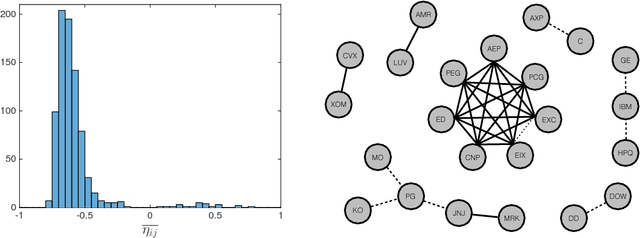
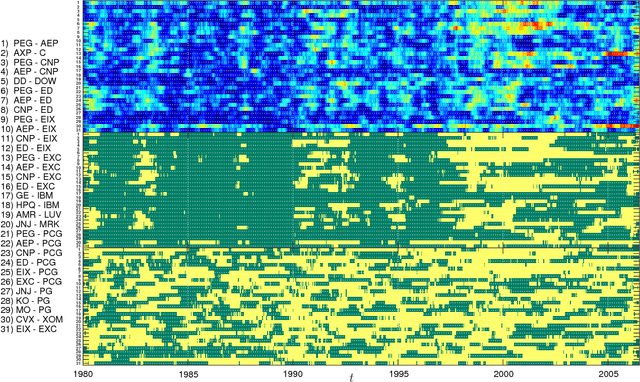
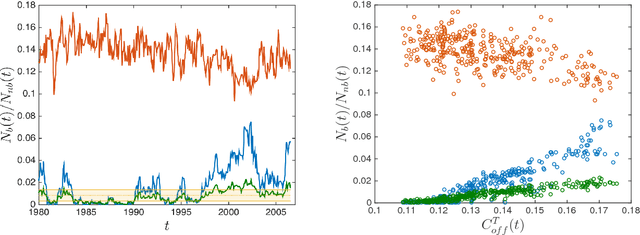
We propose a method for recovering the structure of a sparse undirected graphical model when very few samples are available. The method decides about the presence or absence of bonds between pairs of variable by considering one pair at a time and using a closed form formula, analytically derived by calculating the posterior probability for every possible model explaining a two body system using Jeffreys prior. The approach does not rely on the optimisation of any cost functions and consequently is much faster than existing algorithms. Despite this time and computational advantage, numerical results show that for several sparse topologies the algorithm is comparable to the best existing algorithms, and is more accurate in the presence of hidden variables. We apply this approach to the analysis of US stock market data and to neural data, in order to show its efficiency in recovering robust statistical dependencies in real data with non stationary correlations in time and space.

Variational perturbation and extended Plefka approaches to dynamics on random networks: the case of the kinetic Ising model

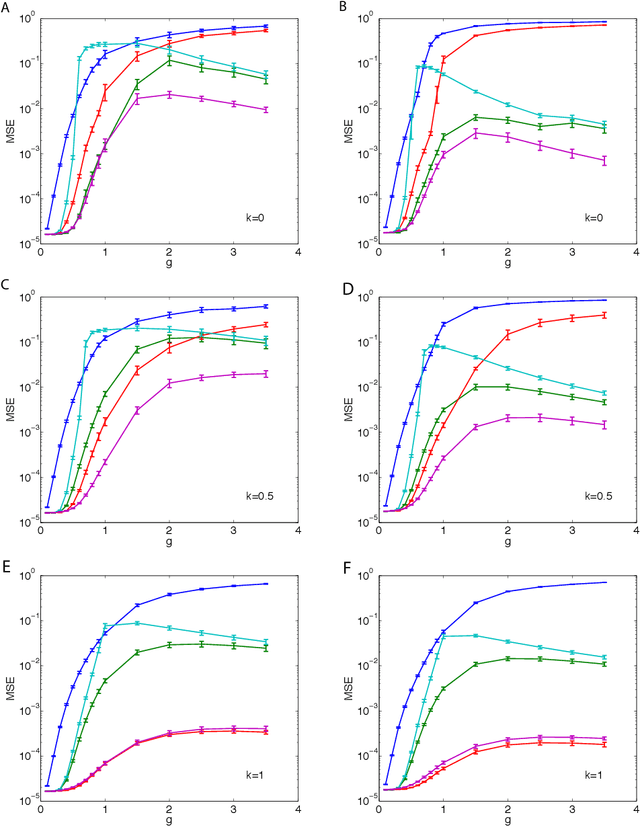
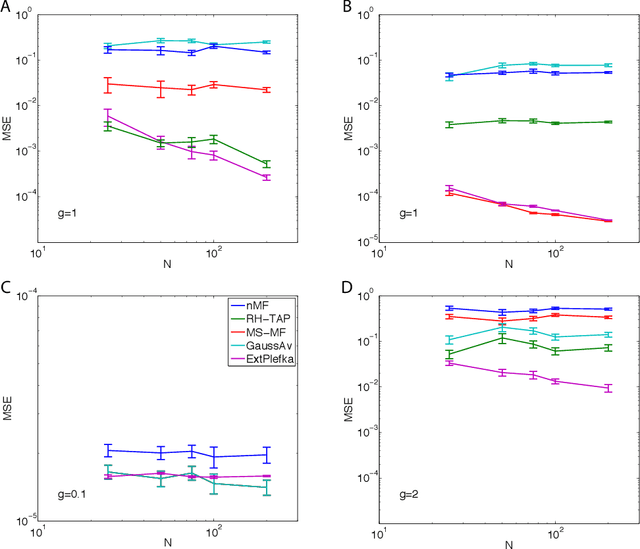
We describe and analyze some novel approaches for studying the dynamics of Ising spin glass models. We first briefly consider the variational approach based on minimizing the Kullback-Leibler divergence between independent trajectories and the real ones and note that this approach only coincides with the mean field equations from the saddle point approximation to the generating functional when the dynamics is defined through a logistic link function, which is the case for the kinetic Ising model with parallel update. We then spend the rest of the paper developing two ways of going beyond the saddle point approximation to the generating functional. In the first one, we develop a variational perturbative approximation to the generating functional by expanding the action around a quadratic function of the local fields and conjugate local fields whose parameters are optimized. We derive analytical expressions for the optimal parameters and show that when the optimization is suitably restricted, we recover the mean field equations that are exact for the fully asymmetric random couplings (M\'ezard and Sakellariou, 2011). However, without this restriction the results are different. We also describe an extended Plefka expansion in which in addition to the magnetization, we also fix the correlation and response functions. Finally, we numerically study the performance of these approximations for Sherrington-Kirkpatrick type couplings for various coupling strengths, degrees of coupling symmetry and external fields. We show that the dynamical equations derived from the extended Plefka expansion outperform the others in all regimes, although it is computationally more demanding. The unconstrained variational approach does not perform well in the small coupling regime, while it approaches dynamical TAP equations of (Roudi and Hertz, 2011) for strong couplings.

Learning with hidden variables

Learning and inferring features that generate sensory input is a task continuously performed by cortex. In recent years, novel algorithms and learning rules have been proposed that allow neural network models to learn such features from natural images, written text, audio signals, etc. These networks usually involve deep architectures with many layers of hidden neurons. Here we review recent advancements in this area emphasizing, amongst other things, the processing of dynamical inputs by networks with hidden nodes and the role of single neuron models. These points and the questions they arise can provide conceptual advancements in understanding of learning in the cortex and the relationship between machine learning approaches to learning with hidden nodes and those in cortical circuits.