Sparse model selection in the highly under-sampled regime
Paper and Code
Jan 02, 2017
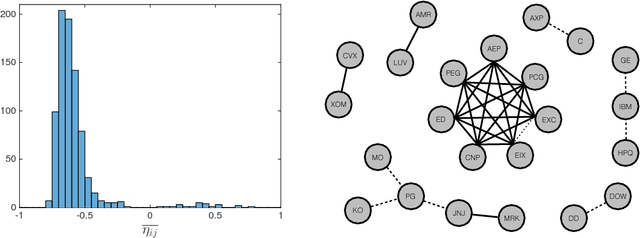
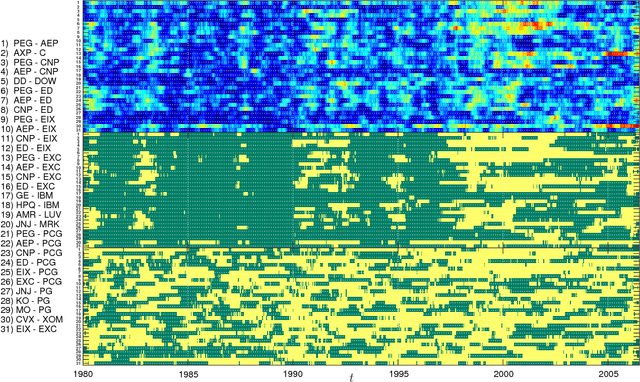
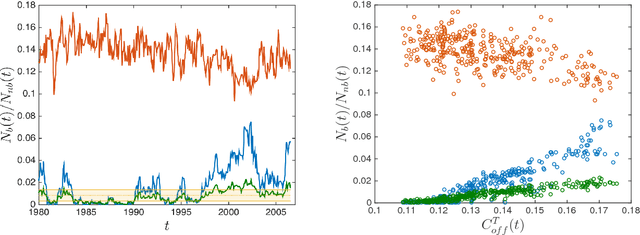
We propose a method for recovering the structure of a sparse undirected graphical model when very few samples are available. The method decides about the presence or absence of bonds between pairs of variable by considering one pair at a time and using a closed form formula, analytically derived by calculating the posterior probability for every possible model explaining a two body system using Jeffreys prior. The approach does not rely on the optimisation of any cost functions and consequently is much faster than existing algorithms. Despite this time and computational advantage, numerical results show that for several sparse topologies the algorithm is comparable to the best existing algorithms, and is more accurate in the presence of hidden variables. We apply this approach to the analysis of US stock market data and to neural data, in order to show its efficiency in recovering robust statistical dependencies in real data with non stationary correlations in time and space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge