Restricted Boltzmann Machines as Models of Interacting Variables

We study the type of distributions that Restricted Boltzmann Machines (RBMs) with different activation functions can express by investigating the effect of the activation function of the hidden nodes on the marginal distribution they impose on observed binary nodes. We report an exact expression for these marginals in the form of a model of interacting binary variables with the explicit form of the interactions depending on the hidden node activation function. We study the properties of these interactions in detail and evaluate how the accuracy with which the RBM approximates distributions over binary variables depends on the hidden node activation function and on the number of hidden nodes. When the inferred RBM parameters are weak, an intuitive pattern is found for the expression of the interaction terms which reduces substantially the differences across activation functions. We show that the weak parameter approximation is a good approximation for different RBMs trained on the MNIST dataset. Interestingly, in these cases, the mapping reveals that the inferred models are essentially low order interaction models.

On the complexity of logistic regression models

We investigate the complexity of logistic regression models which is defined by counting the number of indistinguishable distributions that the model can represent (Balasubramanian, 1997). We find that the complexity of logistic models with binary inputs does not only depend on the number of parameters but also on the distribution of inputs in a non-trivial way which standard treatments of complexity do not address. In particular, we observe that correlations among inputs induce effective dependencies among parameters thus constraining the model and, consequently, reducing its complexity. We derive simple relations for the upper and lower bounds of the complexity. Furthermore, we show analytically that, defining the model parameters on a finite support rather than the entire axis, decreases the complexity in a manner that critically depends on the size of the domain. Based on our findings, we propose a novel model selection criterion which takes into account the entropy of the input distribution. We test our proposal on the problem of selecting the input variables of a logistic regression model in a Bayesian Model Selection framework. In our numerical tests, we find that, while the reconstruction errors of standard model selection approaches (AIC, BIC, $\ell_1$ regularization) strongly depend on the sparsity of the ground truth, the reconstruction error of our method is always close to the minimum in all conditions of sparsity, data size and strength of input correlations. Finally, we observe that, when considering categorical instead of binary inputs, in a simple and mathematically tractable case, the contribution of the alphabet size to the complexity is very small compared to that of parameter space dimension. We further explore the issue by analysing the dataset of the "13 keys to the White House" which is a method for forecasting the outcomes of US presidential elections.

Sparse model selection in the highly under-sampled regime

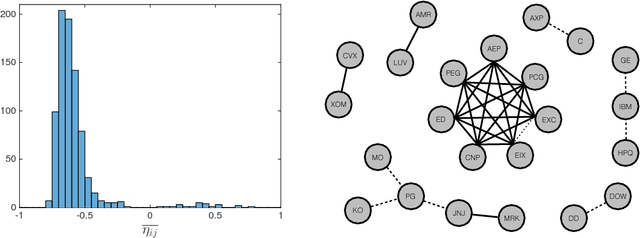
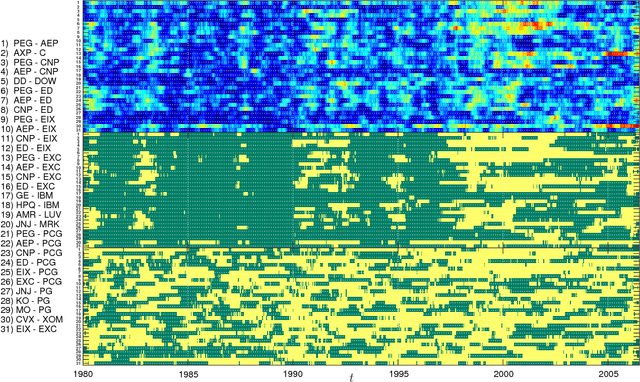
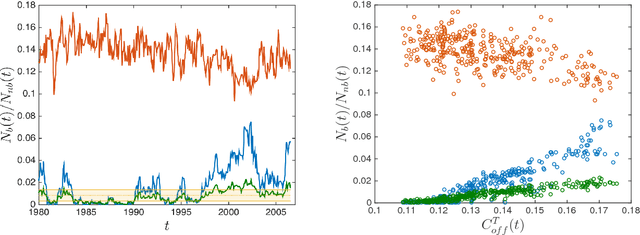
We propose a method for recovering the structure of a sparse undirected graphical model when very few samples are available. The method decides about the presence or absence of bonds between pairs of variable by considering one pair at a time and using a closed form formula, analytically derived by calculating the posterior probability for every possible model explaining a two body system using Jeffreys prior. The approach does not rely on the optimisation of any cost functions and consequently is much faster than existing algorithms. Despite this time and computational advantage, numerical results show that for several sparse topologies the algorithm is comparable to the best existing algorithms, and is more accurate in the presence of hidden variables. We apply this approach to the analysis of US stock market data and to neural data, in order to show its efficiency in recovering robust statistical dependencies in real data with non stationary correlations in time and space.