Resolution and Relevance Trade-offs in Deep Learning
Paper and Code
Mar 20, 2018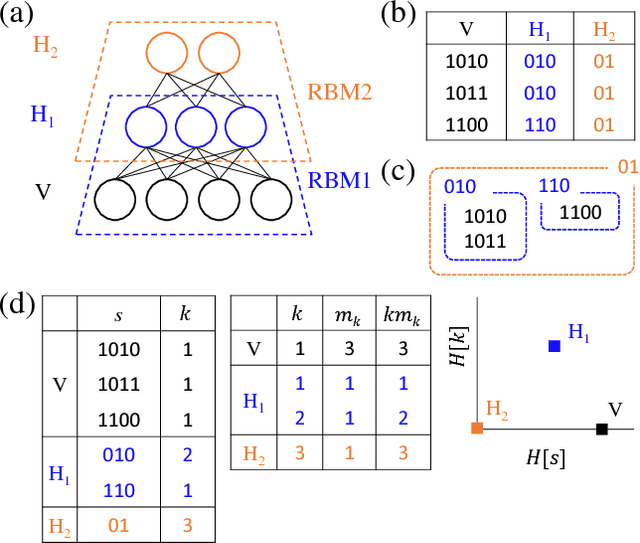
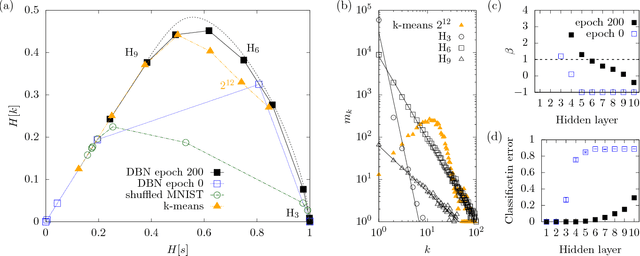
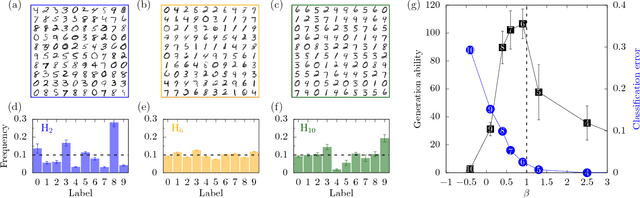
Deep learning has been successfully applied to various tasks, but its underlying mechanism remains unclear. Neural networks associate similar inputs in the visible layer to the same state of hidden variables in deep layers. The fraction of inputs that are associated to the same state is a natural measure of similarity and is simply related to the cost in bits required to represent these inputs. The degeneracy of states with the same information cost provides instead a natural measure of noise and is simply related the entropy of the frequency of states, that we call relevance. Representations with minimal noise, at a given level of similarity (resolution), are those that maximise the relevance. A signature of such efficient representations is that frequency distributions follow power laws. We show, in extensive numerical experiments, that deep neural networks extract a hierarchy of efficient representations from data, because they i) achieve low levels of noise (i.e. high relevance) and ii) exhibit power law distributions. We also find that the layer that is most efficient to reliably generate patterns of training data is the one for which relevance and resolution are traded at the same price, which implies that frequency distribution follows Zipf's law.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge