Junghyo Jo
Stochastic Clock Attention for Aligning Continuous and Ordered Sequences
Sep 18, 2025Abstract:We formulate an attention mechanism for continuous and ordered sequences that explicitly functions as an alignment model, which serves as the core of many sequence-to-sequence tasks. Standard scaled dot-product attention relies on positional encodings and masks but does not enforce continuity or monotonicity, which are crucial for frame-synchronous targets. We propose learned nonnegative \emph{clocks} to source and target and model attention as the meeting probability of these clocks; a path-integral derivation yields a closed-form, Gaussian-like scoring rule with an intrinsic bias toward causal, smooth, near-diagonal alignments, without external positional regularizers. The framework supports two complementary regimes: normalized clocks for parallel decoding when a global length is available, and unnormalized clocks for autoregressive decoding -- both nearly-parameter-free, drop-in replacements. In a Transformer text-to-speech testbed, this construction produces more stable alignments and improved robustness to global time-scaling while matching or improving accuracy over scaled dot-product baselines. We hypothesize applicability to other continuous targets, including video and temporal signal modeling.
Multiplicative Learning
Mar 13, 2025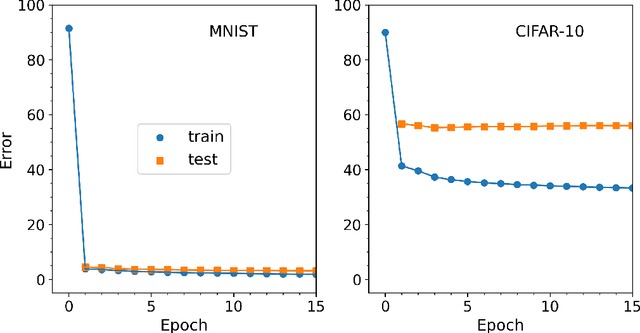
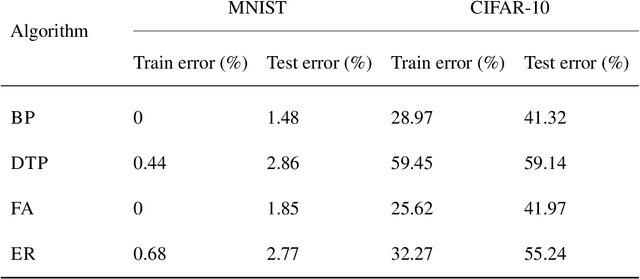
Abstract:Efficient training of artificial neural networks remains a key challenge in deep learning. Backpropagation (BP), the standard learning algorithm, relies on gradient descent and typically requires numerous iterations for convergence. In this study, we introduce Expectation Reflection (ER), a novel learning approach that updates weights multiplicatively based on the ratio of observed to predicted outputs. Unlike traditional methods, ER maintains consistency without requiring ad hoc loss functions or learning rate hyperparameters. We extend ER to multilayer networks and demonstrate its effectiveness in performing image classification tasks. Notably, ER achieves optimal weight updates in a single iteration. Additionally, we reinterpret ER as a modified form of gradient descent incorporating the inverse mapping of target propagation. These findings suggest that ER provides an efficient and scalable alternative for training neural networks.
Data augmentation using diffusion models to enhance inverse Ising inference
Mar 13, 2025Abstract:Identifying model parameters from observed configurations poses a fundamental challenge in data science, especially with limited data. Recently, diffusion models have emerged as a novel paradigm in generative machine learning, capable of producing new samples that closely mimic observed data. These models learn the gradient of model probabilities, bypassing the need for cumbersome calculations of partition functions across all possible configurations. We explore whether diffusion models can enhance parameter inference by augmenting small datasets. Our findings demonstrate this potential through a synthetic task involving inverse Ising inference and a real-world application of reconstructing missing values in neural activity data. This study serves as a proof-of-concept for using diffusion models for data augmentation in physics-related problems, thereby opening new avenues in data science.
Neural Graph Simulator for Complex Systems
Nov 14, 2024Abstract:Numerical simulation is a predominant tool for studying the dynamics in complex systems, but large-scale simulations are often intractable due to computational limitations. Here, we introduce the Neural Graph Simulator (NGS) for simulating time-invariant autonomous systems on graphs. Utilizing a graph neural network, the NGS provides a unified framework to simulate diverse dynamical systems with varying topologies and sizes without constraints on evaluation times through its non-uniform time step and autoregressive approach. The NGS offers significant advantages over numerical solvers by not requiring prior knowledge of governing equations and effectively handling noisy or missing data with a robust training scheme. It demonstrates superior computational efficiency over conventional methods, improving performance by over $10^5$ times in stiff problems. Furthermore, it is applied to real traffic data, forecasting traffic flow with state-of-the-art accuracy. The versatility of the NGS extends beyond the presented cases, offering numerous potential avenues for enhancement.
Geometric Remove-and-Retrain (GOAR): Coordinate-Invariant eXplainable AI Assessment
Jul 17, 2024Abstract:Identifying the relevant input features that have a critical influence on the output results is indispensable for the development of explainable artificial intelligence (XAI). Remove-and-Retrain (ROAR) is a widely accepted approach for assessing the importance of individual pixels by measuring changes in accuracy following their removal and subsequent retraining of the modified dataset. However, we uncover notable limitations in pixel-perturbation strategies. When viewed from a geometric perspective, we discover that these metrics fail to discriminate between differences among feature attribution methods, thereby compromising the reliability of the evaluation. To address this challenge, we introduce an alternative feature-perturbation approach named Geometric Remove-and-Retrain (GOAR). Through a series of experiments with both synthetic and real datasets, we substantiate that GOAR transcends the limitations of pixel-centric metrics.
Upsample Guidance: Scale Up Diffusion Models without Training
Apr 02, 2024Abstract:Diffusion models have demonstrated superior performance across various generative tasks including images, videos, and audio. However, they encounter difficulties in directly generating high-resolution samples. Previously proposed solutions to this issue involve modifying the architecture, further training, or partitioning the sampling process into multiple stages. These methods have the limitation of not being able to directly utilize pre-trained models as-is, requiring additional work. In this paper, we introduce upsample guidance, a technique that adapts pretrained diffusion model (e.g., $512^2$) to generate higher-resolution images (e.g., $1536^2$) by adding only a single term in the sampling process. Remarkably, this technique does not necessitate any additional training or relying on external models. We demonstrate that upsample guidance can be applied to various models, such as pixel-space, latent space, and video diffusion models. We also observed that the proper selection of guidance scale can improve image quality, fidelity, and prompt alignment.
GNRK: Graph Neural Runge-Kutta method for solving partial differential equations
Oct 01, 2023Abstract:Neural networks have proven to be efficient surrogate models for tackling partial differential equations (PDEs). However, their applicability is often confined to specific PDEs under certain constraints, in contrast to classical PDE solvers that rely on numerical differentiation. Striking a balance between efficiency and versatility, this study introduces a novel approach called Graph Neural Runge-Kutta (GNRK), which integrates graph neural network modules with a recurrent structure inspired by the classical solvers. The GNRK operates on graph structures, ensuring its resilience to changes in spatial and temporal resolutions during domain discretization. Moreover, it demonstrates the capability to address general PDEs, irrespective of initial conditions or PDE coefficients. To assess its performance, we benchmark the GNRK against existing neural network based PDE solvers using the 2-dimensional Burgers' equation, revealing the GNRK's superiority in terms of model size and accuracy. Additionally, this graph-based methodology offers a straightforward extension for solving coupled differential equations, typically necessitating more intricate models.
Understanding the Latent Space of Diffusion Models through the Lens of Riemannian Geometry
Jul 24, 2023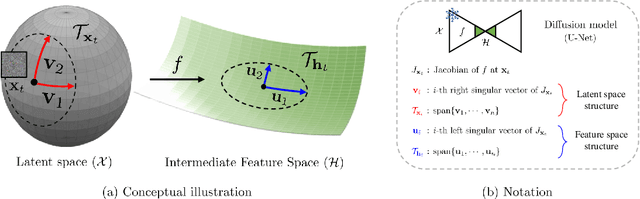
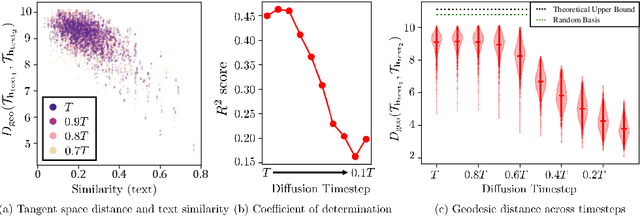

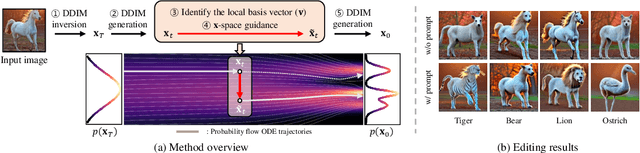
Abstract:Despite the success of diffusion models (DMs), we still lack a thorough understanding of their latent space. To understand the latent space $\mathbf{x}_t \in \mathcal{X}$, we analyze them from a geometrical perspective. Specifically, we utilize the pullback metric to find the local latent basis in $\mathcal{X}$ and their corresponding local tangent basis in $\mathcal{H}$, the intermediate feature maps of DMs. The discovered latent basis enables unsupervised image editing capability through latent space traversal. We investigate the discovered structure from two perspectives. First, we examine how geometric structure evolves over diffusion timesteps. Through analysis, we show that 1) the model focuses on low-frequency components early in the generative process and attunes to high-frequency details later; 2) At early timesteps, different samples share similar tangent spaces; and 3) The simpler datasets that DMs trained on, the more consistent the tangent space for each timestep. Second, we investigate how the geometric structure changes based on text conditioning in Stable Diffusion. The results show that 1) similar prompts yield comparable tangent spaces; and 2) the model depends less on text conditions in later timesteps. To the best of our knowledge, this paper is the first to present image editing through $\mathbf{x}$-space traversal and provide thorough analyses of the latent structure of DMs.
Tradeoff of generalization error in unsupervised learning
Mar 10, 2023Abstract:Finding the optimal model complexity that minimizes the generalization error (GE) is a key issue of machine learning. For the conventional supervised learning, this task typically involves the bias-variance tradeoff: lowering the bias by making the model more complex entails an increase in the variance. Meanwhile, little has been studied about whether the same tradeoff exists for unsupervised learning. In this study, we propose that unsupervised learning generally exhibits a two-component tradeoff of the GE, namely the model error and the data error -- using a more complex model reduces the model error at the cost of the data error, with the data error playing a more significant role for a smaller training dataset. This is corroborated by training the restricted Boltzmann machine to generate the configurations of the two-dimensional Ising model at a given temperature and the totally asymmetric simple exclusion process with given entry and exit rates. Our results also indicate that the optimal model tends to be more complex when the data to be learned are more complex.
Unsupervised Discovery of Semantic Latent Directions in Diffusion Models
Feb 24, 2023Abstract:Despite the success of diffusion models (DMs), we still lack a thorough understanding of their latent space. While image editing with GANs builds upon latent space, DMs rely on editing the conditions such as text prompts. We present an unsupervised method to discover interpretable editing directions for the latent variables $\mathbf{x}_t \in \mathcal{X}$ of DMs. Our method adopts Riemannian geometry between $\mathcal{X}$ and the intermediate feature maps $\mathcal{H}$ of the U-Nets to provide a deep understanding over the geometrical structure of $\mathcal{X}$. The discovered semantic latent directions mostly yield disentangled attribute changes, and they are globally consistent across different samples. Furthermore, editing in earlier timesteps edits coarse attributes, while ones in later timesteps focus on high-frequency details. We define the curvedness of a line segment between samples to show that $\mathcal{X}$ is a curved manifold. Experiments on different baselines and datasets demonstrate the effectiveness of our method even on Stable Diffusion. Our source code will be publicly available for the future researchers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge