Neural Graph Simulator for Complex Systems

Numerical simulation is a predominant tool for studying the dynamics in complex systems, but large-scale simulations are often intractable due to computational limitations. Here, we introduce the Neural Graph Simulator (NGS) for simulating time-invariant autonomous systems on graphs. Utilizing a graph neural network, the NGS provides a unified framework to simulate diverse dynamical systems with varying topologies and sizes without constraints on evaluation times through its non-uniform time step and autoregressive approach. The NGS offers significant advantages over numerical solvers by not requiring prior knowledge of governing equations and effectively handling noisy or missing data with a robust training scheme. It demonstrates superior computational efficiency over conventional methods, improving performance by over $10^5$ times in stiff problems. Furthermore, it is applied to real traffic data, forecasting traffic flow with state-of-the-art accuracy. The versatility of the NGS extends beyond the presented cases, offering numerous potential avenues for enhancement.

GNRK: Graph Neural Runge-Kutta method for solving partial differential equations

Neural networks have proven to be efficient surrogate models for tackling partial differential equations (PDEs). However, their applicability is often confined to specific PDEs under certain constraints, in contrast to classical PDE solvers that rely on numerical differentiation. Striking a balance between efficiency and versatility, this study introduces a novel approach called Graph Neural Runge-Kutta (GNRK), which integrates graph neural network modules with a recurrent structure inspired by the classical solvers. The GNRK operates on graph structures, ensuring its resilience to changes in spatial and temporal resolutions during domain discretization. Moreover, it demonstrates the capability to address general PDEs, irrespective of initial conditions or PDE coefficients. To assess its performance, we benchmark the GNRK against existing neural network based PDE solvers using the 2-dimensional Burgers' equation, revealing the GNRK's superiority in terms of model size and accuracy. Additionally, this graph-based methodology offers a straightforward extension for solving coupled differential equations, typically necessitating more intricate models.

Scale-invariant representation of machine learning

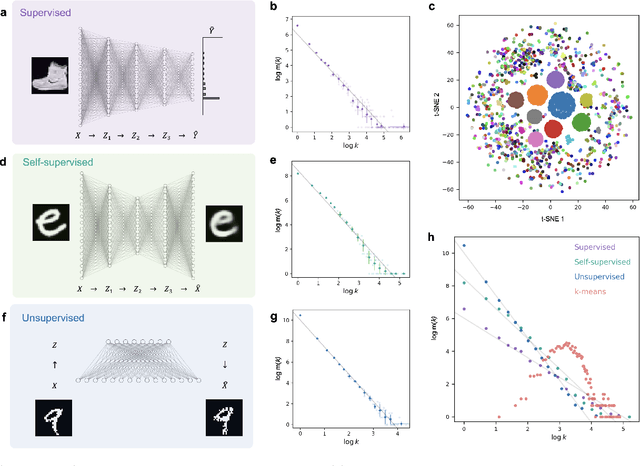
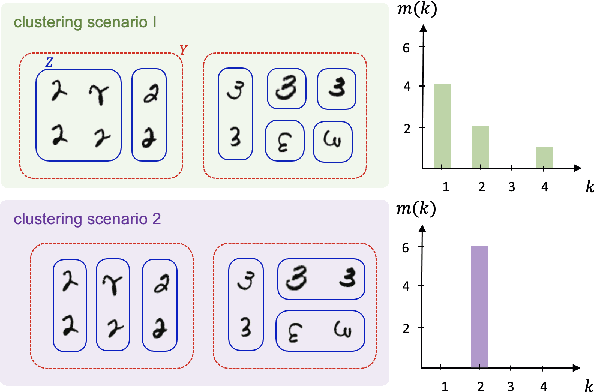
The success of machine learning stems from its structured data representation. Similar data have close representation as compressed codes for classification or emerged labels for clustering. We observe that the frequency of the internal representation follows power laws in both supervised and unsupervised learning. The scale-invariant distribution implies that machine learning largely compresses frequent typical data, and at the same time, differentiates many atypical data as outliers. In this study, we derive how the power laws can naturally arise in machine learning. In terms of information theory, the scale-invariant representation corresponds to a maximally uncertain data grouping among possible representations that guarantee pre-specified learning accuracy.

Compression phase is not necessary for generalization in representation learning

The outstanding performance of deep learning in various fields has been a fundamental query, which can be potentially examined using information theory that interprets the learning process as the transmission and compression of information. Information plane analyses of the mutual information between the input-hidden-output layers demonstrated two distinct learning phases of fitting and compression. It is debatable if the compression phase is necessary to generalize the input-output relations extracted from training data. In this study, we investigated this through experiments with various species of autoencoders and evaluated their information processing phase with an accurate kernel-based estimator of mutual information. Given sufficient training data, vanilla autoencoders demonstrated the compression phase, which was amplified after imposing sparsity regularization for hidden activities. However, we found that the compression phase is not universally observed in different species of autoencoders, including variational autoencoders, that have special constraints on network weights or manifold of hidden space. These types of autoencoders exhibited perfect generalization ability for test data without requiring the compression phase. Thus, we conclude that the compression phase is not necessary for generalization in representation learning.