Scale-invariant representation of machine learning
Paper and Code
Sep 07, 2021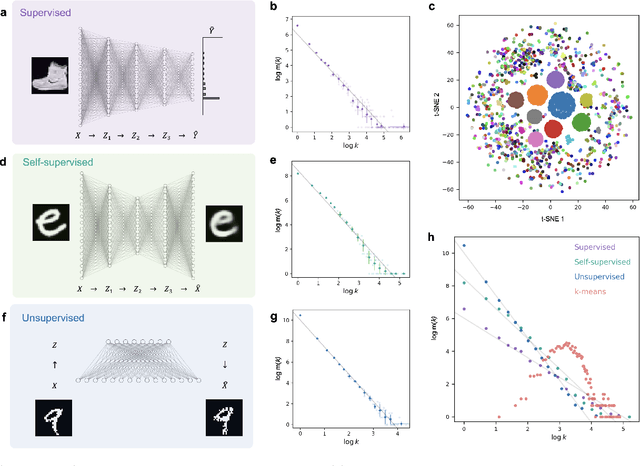
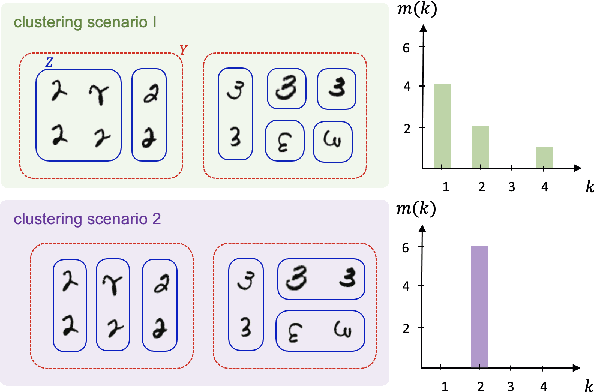
The success of machine learning stems from its structured data representation. Similar data have close representation as compressed codes for classification or emerged labels for clustering. We observe that the frequency of the internal representation follows power laws in both supervised and unsupervised learning. The scale-invariant distribution implies that machine learning largely compresses frequent typical data, and at the same time, differentiates many atypical data as outliers. In this study, we derive how the power laws can naturally arise in machine learning. In terms of information theory, the scale-invariant representation corresponds to a maximally uncertain data grouping among possible representations that guarantee pre-specified learning accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge