Multiplicative Learning

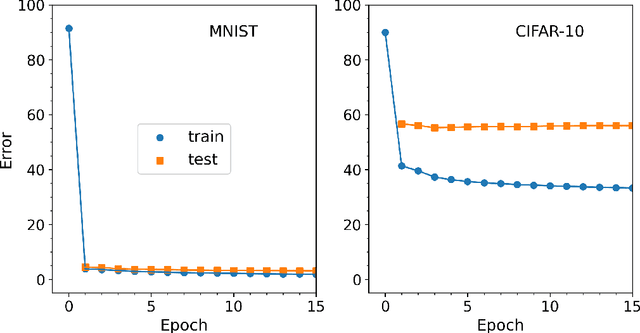
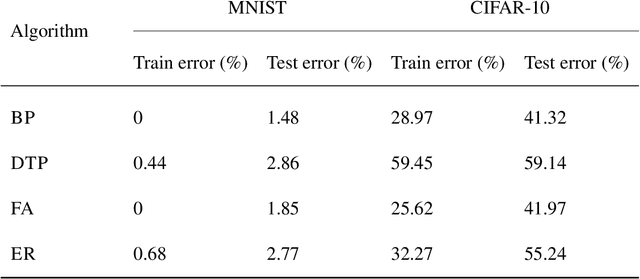
Efficient training of artificial neural networks remains a key challenge in deep learning. Backpropagation (BP), the standard learning algorithm, relies on gradient descent and typically requires numerous iterations for convergence. In this study, we introduce Expectation Reflection (ER), a novel learning approach that updates weights multiplicatively based on the ratio of observed to predicted outputs. Unlike traditional methods, ER maintains consistency without requiring ad hoc loss functions or learning rate hyperparameters. We extend ER to multilayer networks and demonstrate its effectiveness in performing image classification tasks. Notably, ER achieves optimal weight updates in a single iteration. Additionally, we reinterpret ER as a modified form of gradient descent incorporating the inverse mapping of target propagation. These findings suggest that ER provides an efficient and scalable alternative for training neural networks.

Tight basis cycle representatives for persistent homology of large data sets

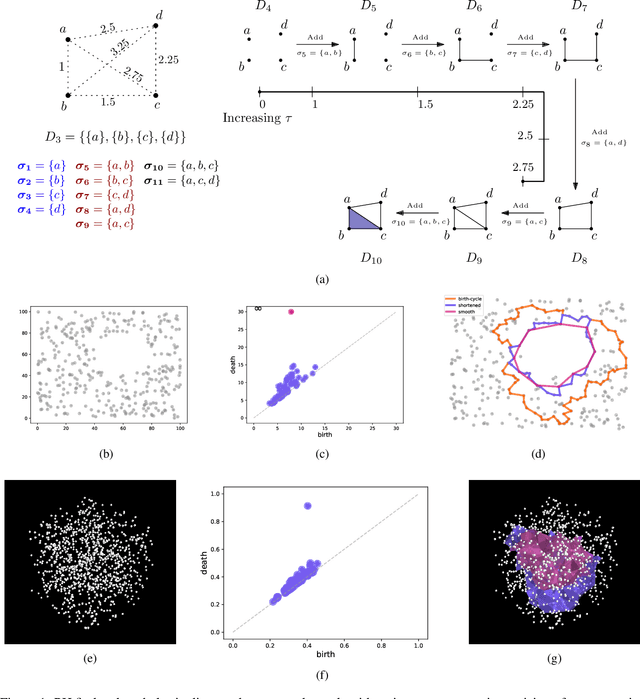
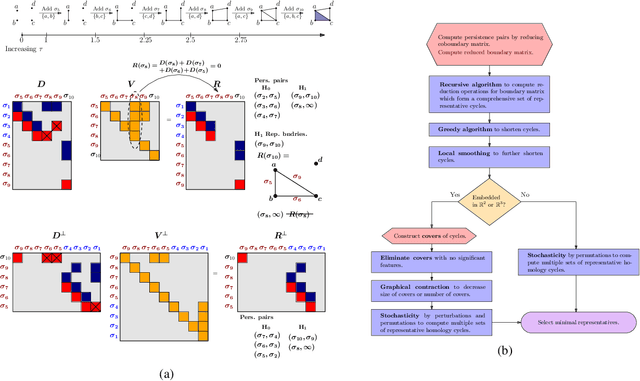
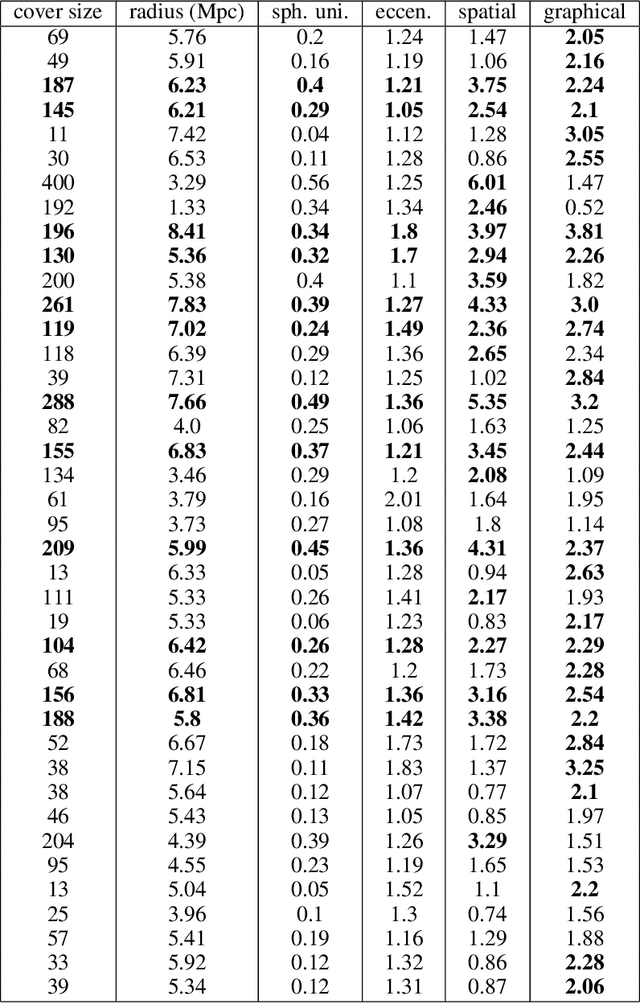
Persistent homology (PH) is a popular tool for topological data analysis that has found applications across diverse areas of research. It provides a rigorous method to compute robust topological features in discrete experimental observations that often contain various sources of uncertainties. Although powerful in theory, PH suffers from high computation cost that precludes its application to large data sets. Additionally, most analyses using PH are limited to computing the existence of nontrivial features. Precise localization of these features is not generally attempted because, by definition, localized representations are not unique and because of even higher computation cost. For scientific applications, such a precise location is a sine qua non for determining functional significance. Here, we provide a strategy and algorithms to compute tight representative boundaries around nontrivial robust features in large data sets. To showcase the efficiency of our algorithms and the precision of computed boundaries, we analyze three data sets from different scientific fields. In the human genome, we found an unexpected effect on loops through chromosome 13 and the sex chromosomes, upon impairment of chromatin loop formation. In a distribution of galaxies in the universe, we found statistically significant voids. In protein homologs with significantly different topology, we found voids attributable to ligand-interaction, mutation, and differences between species.

Dory: Overcoming Barriers to Computing Persistent Homology

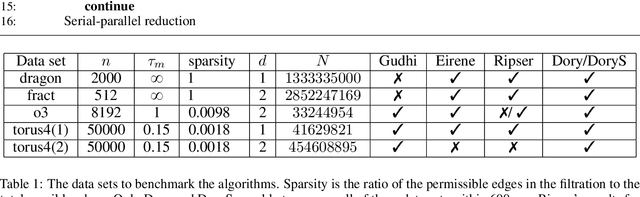
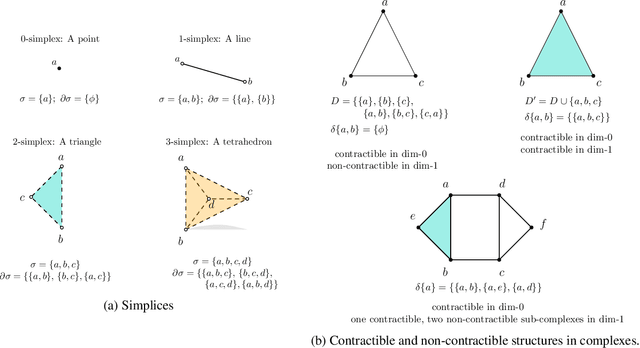
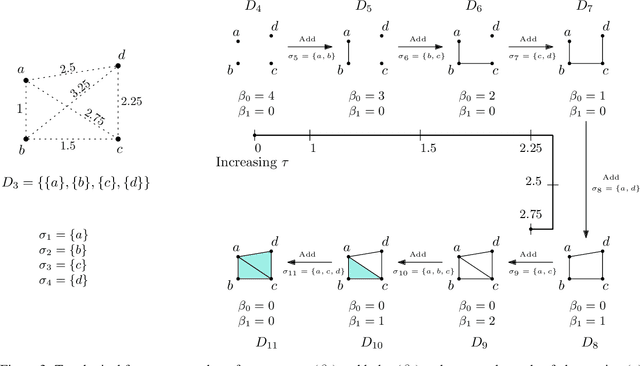
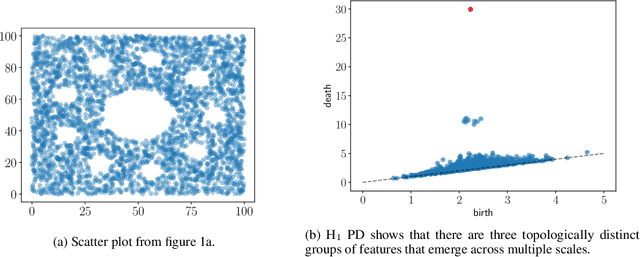
Persistent homology (PH) is an approach to topological data analysis (TDA) that computes multi-scale topologically invariant properties of high-dimensional data that are robust to noise. While PH has revealed useful patterns across various applications, computational requirements have limited applications to small data sets of a few thousand points. We present Dory, an efficient and scalable algorithm that can compute the persistent homology of large data sets. Dory uses significantly less memory than published algorithms and also provides significant reductions in the computation time compared to most algorithms. It scales to process data sets with millions of points. As an application, we compute the PH of the human genome at high resolution as revealed by a genome-wide Hi-C data set. Results show that the topology of the human genome changes significantly upon treatment with auxin, a molecule that degrades cohesin, corroborating the hypothesis that cohesin plays a crucial role in loop formation in DNA.

Inference of stochastic time series with missing data

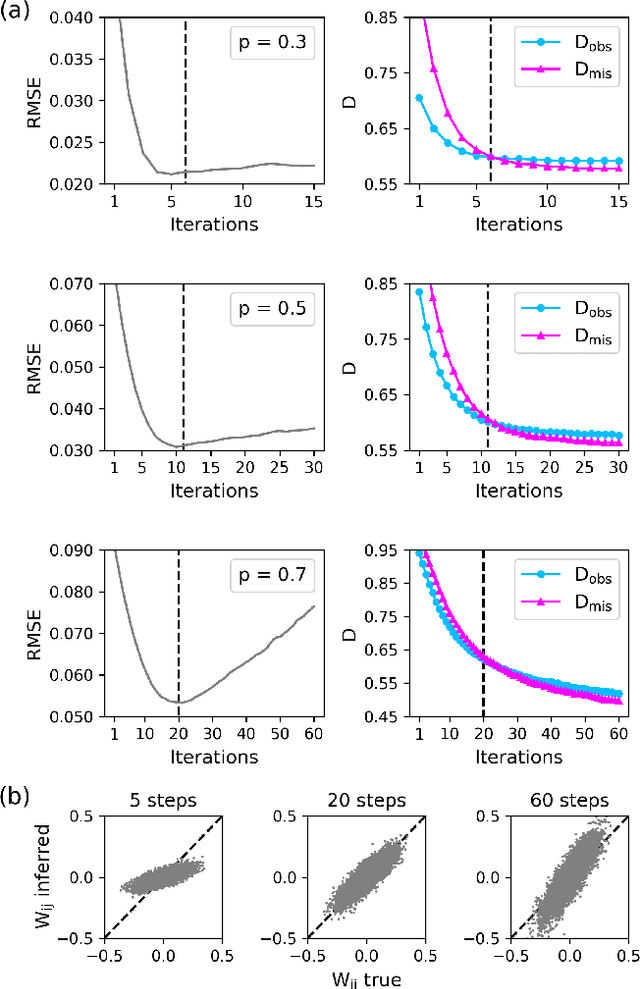
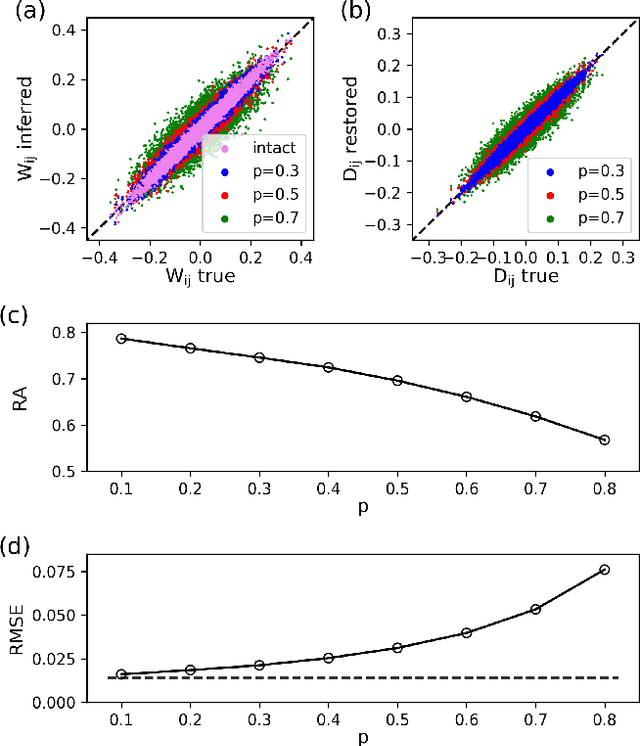
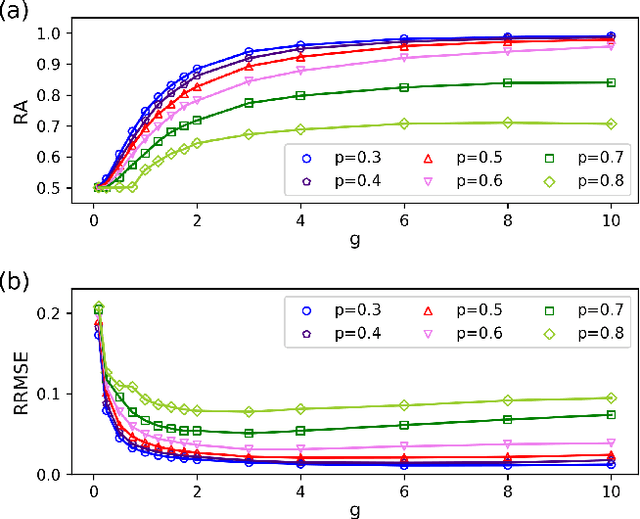
Inferring dynamics from time series is an important objective in data analysis. In particular, it is challenging to infer stochastic dynamics given incomplete data. We propose an expectation maximization (EM) algorithm that iterates between alternating two steps: E-step restores missing data points, while M-step infers an underlying network model of restored data. Using synthetic data generated by a kinetic Ising model, we confirm that the algorithm works for restoring missing data points as well as inferring the underlying model. At the initial iteration of the EM algorithm, the model inference shows better model-data consistency with observed data points than with missing data points. As we keep iterating, however, missing data points show better model-data consistency. We find that demanding equal consistency of observed and missing data points provides an effective stopping criterion for the iteration to prevent overshooting the most accurate model inference. Armed with this EM algorithm with this stopping criterion, we infer missing data points and an underlying network from a time-series data of real neuronal activities. Our method recovers collective properties of neuronal activities, such as time correlations and firing statistics, which have previously never been optimized to fit.

Inverse Ising inference from high-temperature re-weighting of observations

Maximum Likelihood Estimation (MLE) is the bread and butter of system inference for stochastic systems. In some generality, MLE will converge to the correct model in the infinite data limit. In the context of physical approaches to system inference, such as Boltzmann machines, MLE requires the arduous computation of partition functions summing over all configurations, both observed and unobserved. We present here a conceptually and computationally transparent data-driven approach to system inference that is based on the simple question: How should the Boltzmann weights of observed configurations be modified to make the probability distribution of observed configurations close to a flat distribution? This algorithm gives accurate inference by using only observed configurations for systems with a large number of degrees of freedom where other approaches are intractable.