Inference of stochastic time series with missing data
Paper and Code
Jan 28, 2021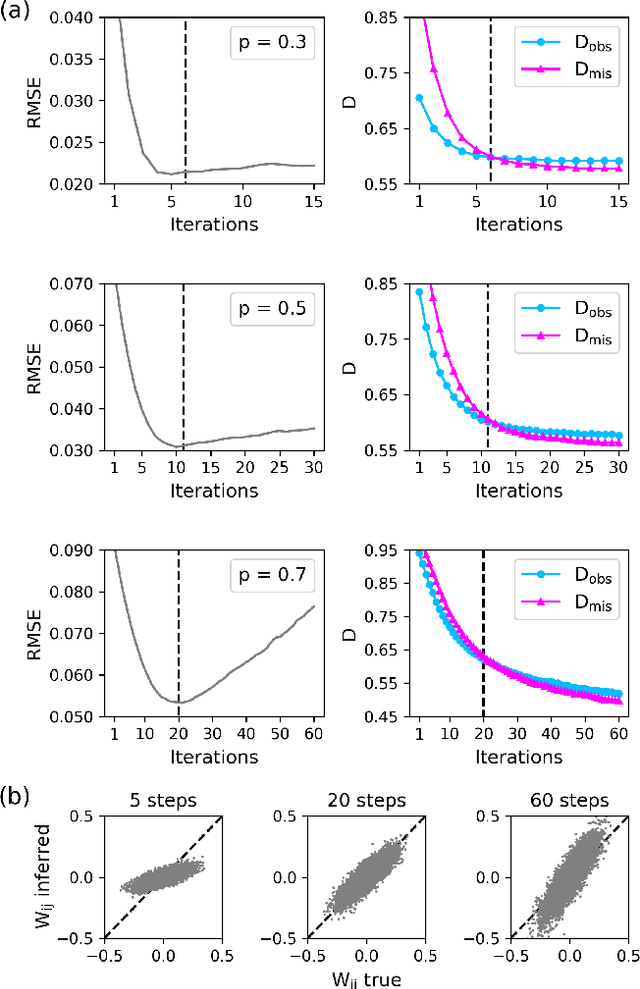
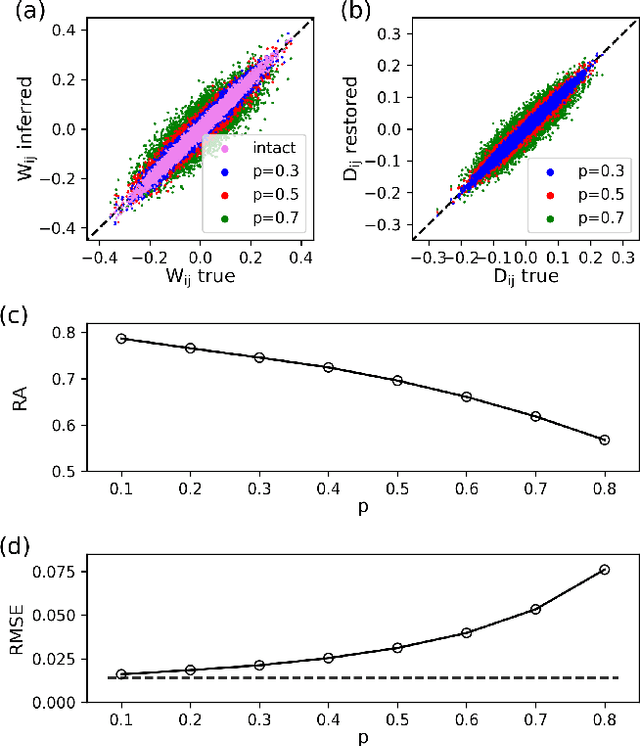
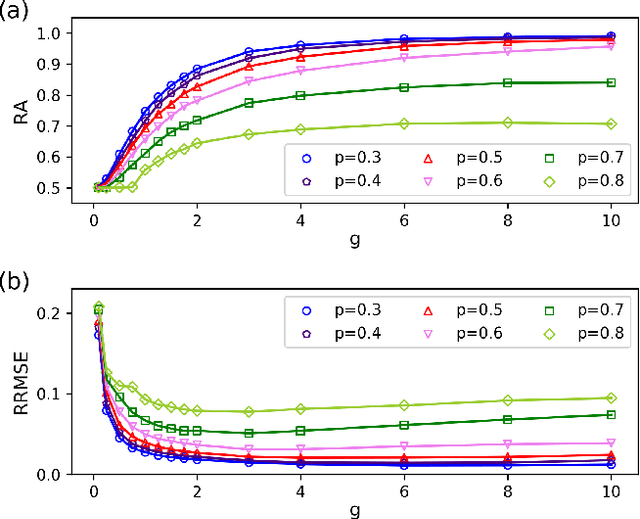
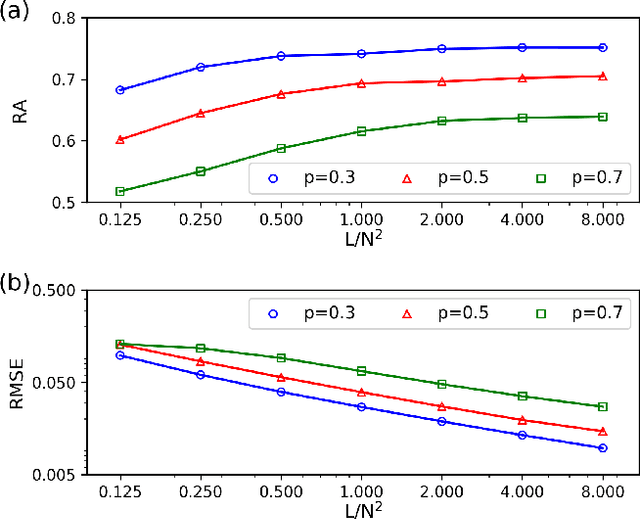
Inferring dynamics from time series is an important objective in data analysis. In particular, it is challenging to infer stochastic dynamics given incomplete data. We propose an expectation maximization (EM) algorithm that iterates between alternating two steps: E-step restores missing data points, while M-step infers an underlying network model of restored data. Using synthetic data generated by a kinetic Ising model, we confirm that the algorithm works for restoring missing data points as well as inferring the underlying model. At the initial iteration of the EM algorithm, the model inference shows better model-data consistency with observed data points than with missing data points. As we keep iterating, however, missing data points show better model-data consistency. We find that demanding equal consistency of observed and missing data points provides an effective stopping criterion for the iteration to prevent overshooting the most accurate model inference. Armed with this EM algorithm with this stopping criterion, we infer missing data points and an underlying network from a time-series data of real neuronal activities. Our method recovers collective properties of neuronal activities, such as time correlations and firing statistics, which have previously never been optimized to fit.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge