Occam learning

We discuss probabilistic neural network models for unsupervised learning where the distribution of the hidden layer is fixed. We argue that learning machines with this architecture enjoy a number of desirable properties. For example, the model can be chosen as a simple and interpretable one, it does not need to be over-parametrised and training is argued to be efficient in a thermodynamic sense. When hidden units are binary variables, these models have a natural interpretation in terms of features. We show that the featureless state corresponds to a state of maximal ignorance about the features and that learning the first feature depends on non-Gaussian statistical properties of the data. We suggest that the distribution of hidden variables should be chosen according to the principle of maximal relevance. We introduce the Hierarchical Feature Model as an example of a model that satisfies this principle, and that encodes an a priori organisation of the feature space. We present extensive numerical experiments in order i) to test that the internal representation of learning machines can indeed be independent of the data with which they are trained and ii) that only a finite number of features are needed to describe a datasets.

A random energy approach to deep learning

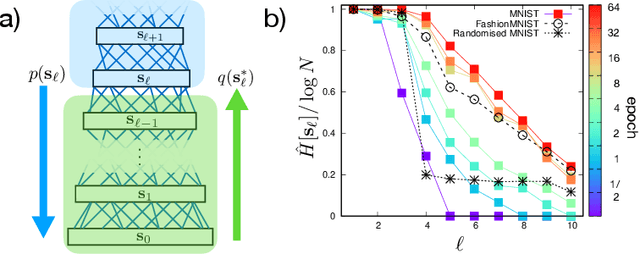
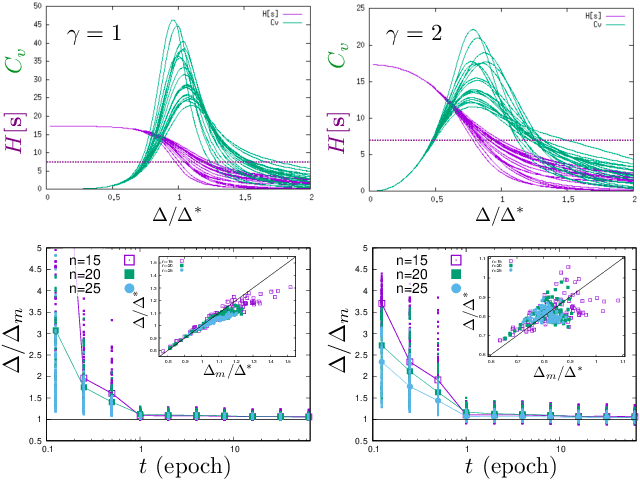
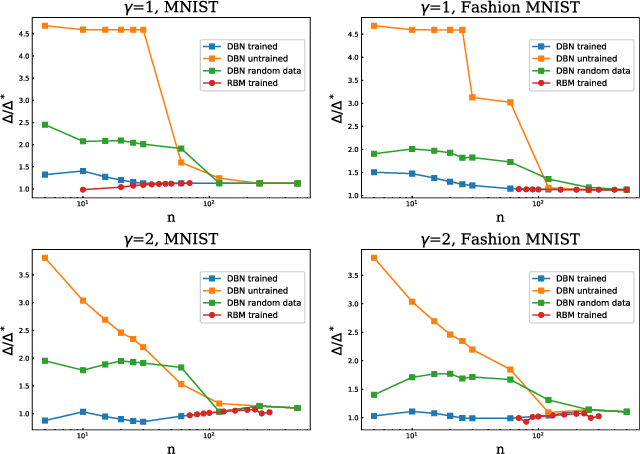
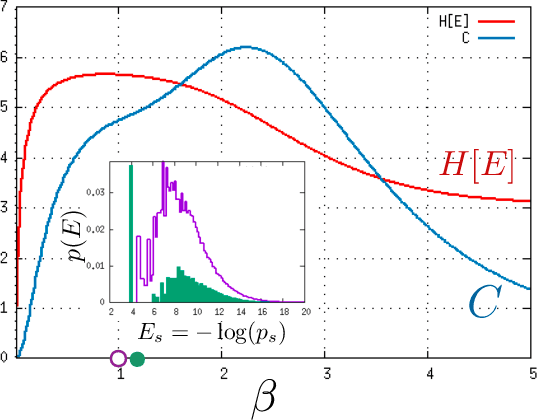
We study a generic ensemble of deep belief networks which is parametrized by the distribution of energy levels of the hidden states of each layer. We show that, within a random energy approach, statistical dependence can propagate from the visible to deep layers only if each layer is tuned close to the critical point during learning. As a consequence, efficiently trained learning machines are characterised by a broad distribution of energy levels. The analysis of Deep Belief Networks and Restricted Boltzmann Machines on different datasets confirms these conclusions.

Active image restoration

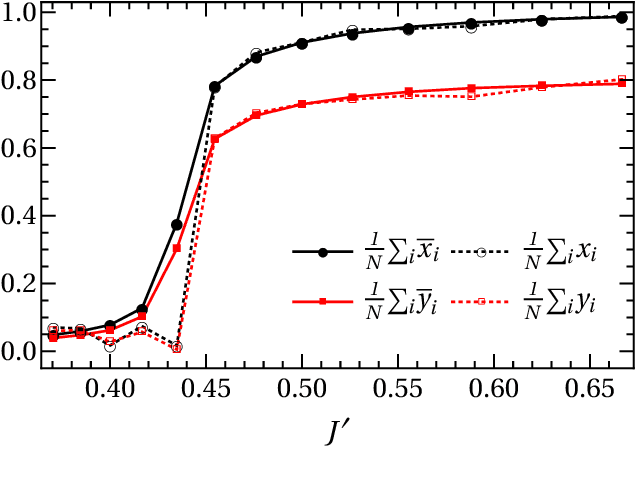
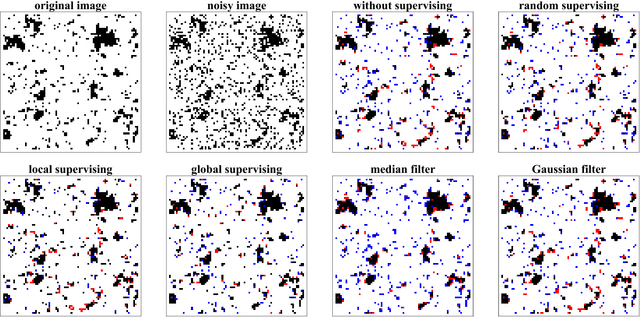
We study active restoration of noise-corrupted images generated via the Gibbs probability of an Ising ferromagnet in external magnetic field. Ferromagnetism accounts for the prior expectation of data smoothness, i.e. a positive correlation between neighbouring pixels (Ising spins), while the magnetic field refers to the bias. The restoration is actively supervised by requesting the true values of certain pixels after a noisy observation. This additional information improves restoration of other pixels. The optimal strategy of active inference is not known for realistic (two-dimensional) images. We determine this strategy for the mean-field version of the model and show that it amounts to supervising the values of spins (pixels) that do not agree with the sign of the average magnetization. The strategy leads to a transparent analytical expression for the minimal Bayesian risk, and shows that there is a maximal number of pixels beyond of which the supervision is useless. We show numerically that this strategy applies for two-dimensional images away from the critical regime. Within this regime the strategy is outperformed by its local (adaptive) version, which supervises pixels that do not agree with their Bayesian estimate. We show on transparent examples how active supervising can be essential in recovering noise-corrupted images and advocate for a wider usage of active methods in image restoration.