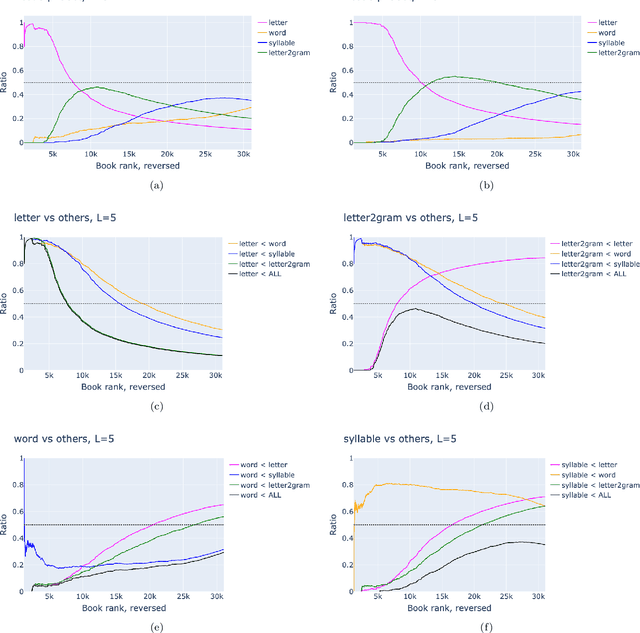
Unsupervised extraction of local and global keywords from a single text

We propose an unsupervised, corpus-independent method to extract keywords from a single text. It is based on the spatial distribution of words and the response of this distribution to a random permutation of words. As compared to existing methods (such as e.g. YAKE) our method has three advantages. First, it is significantly more effective at extracting keywords from long texts. Second, it allows inference of two types of keywords: local and global. Third, it uncovers basic themes in texts. Additionally, our method is language-independent and applies to short texts. The results are obtained via human annotators with previous knowledge of texts from our database of classical literary works (the agreement between annotators is from moderate to substantial). Our results are supported via human-independent arguments based on the average length of extracted content words and on the average number of nouns in extracted words. We discuss relations of keywords with higher-order textual features and reveal a connection between keywords and chapter divisions.

Optimal alphabet for single text compression

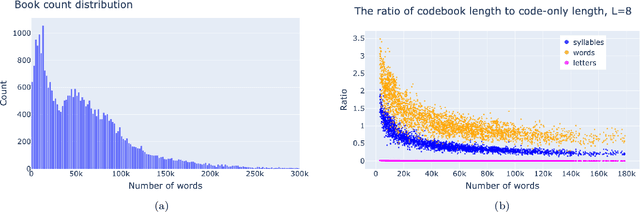
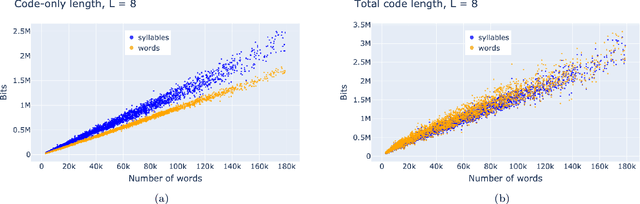
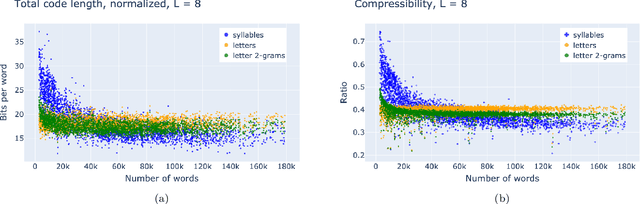
A text can be viewed via different representations, i.e. as a sequence of letters, n-grams of letters, syllables, words, and phrases. Here we study the optimal noiseless compression of texts using the Huffman code, where the alphabet of encoding coincides with one of those representations. We show that it is necessary to account for the codebook when compressing a single text. Hence, the total compression comprises of the optimally compressed text -- characterized by the entropy of the alphabet elements -- and the codebook which is text-specific and therefore has to be included for noiseless (de)compression. For texts of Project Gutenberg the best compression is provided by syllables, i.e. the minimal meaning-expressing element of the language. If only sufficiently short texts are retained, the optimal alphabet is that of letters or 2-grams of letters depending on the retained length.

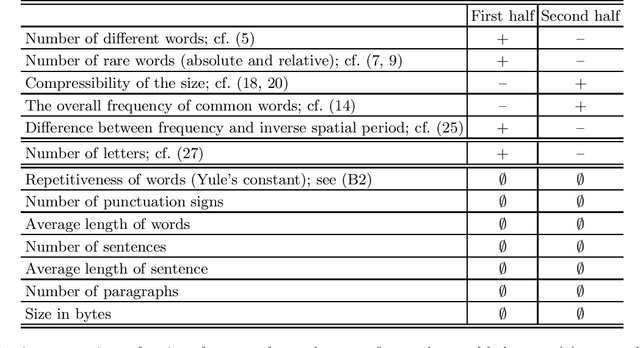
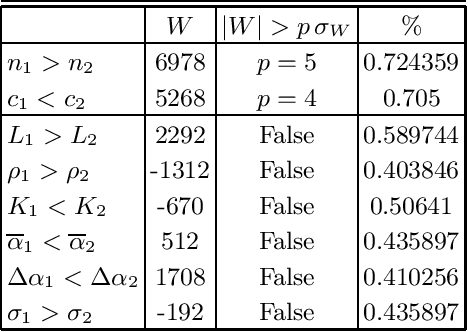
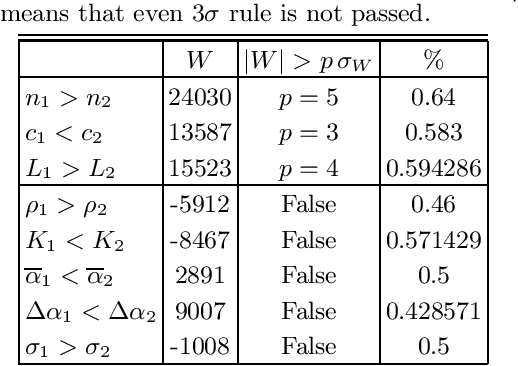
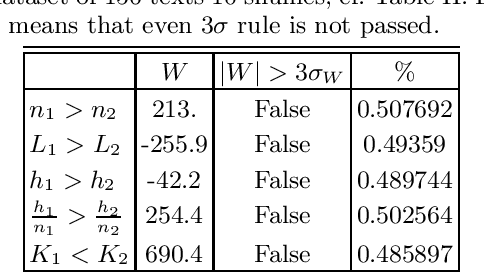
Two halves of a meaningful text are statistically different

Which statistical features distinguish a meaningful text (possibly written in an unknown system) from a meaningless set of symbols? Here we answer this question by comparing features of the first half of a text to its second half. This comparison can uncover hidden effects, because the halves have the same values of many parameters (style, genre {\it etc}). We found that the first half has more different words and more rare words than the second half. Also, words in the first half are distributed less homogeneously over the text in the sense of of the difference between the frequency and the inverse spatial period. These differences hold for the significant majority of several hundred relatively short texts we studied. The statistical significance is confirmed via the Wilcoxon test. Differences disappear after random permutation of words that destroys the linear structure of the text. The differences reveal a temporal asymmetry in meaningful texts, which is confirmed by showing that texts are much better compressible in their natural way (i.e. along the narrative) than in the word-inverted form. We conjecture that these results connect the semantic organization of a text (defined by the flow of its narrative) to its statistical features.

Active image restoration

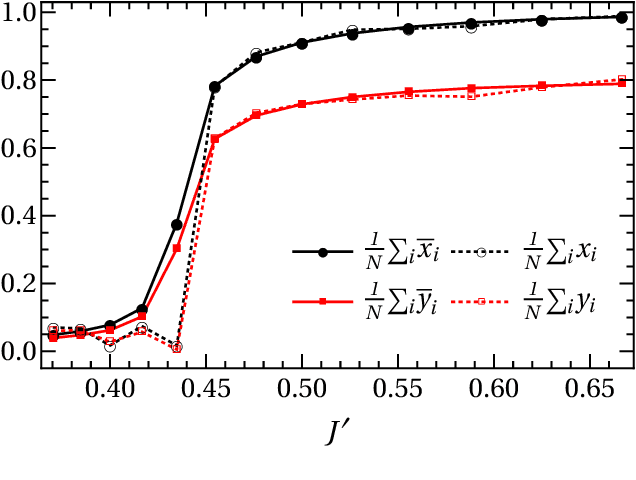
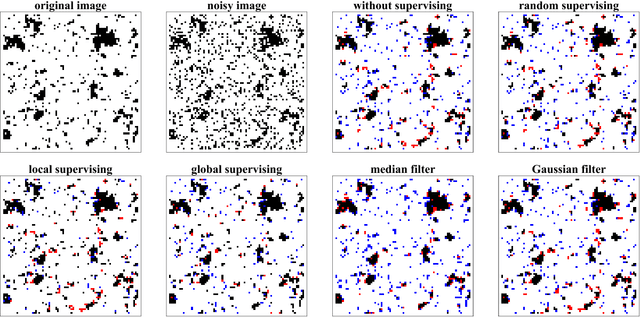
We study active restoration of noise-corrupted images generated via the Gibbs probability of an Ising ferromagnet in external magnetic field. Ferromagnetism accounts for the prior expectation of data smoothness, i.e. a positive correlation between neighbouring pixels (Ising spins), while the magnetic field refers to the bias. The restoration is actively supervised by requesting the true values of certain pixels after a noisy observation. This additional information improves restoration of other pixels. The optimal strategy of active inference is not known for realistic (two-dimensional) images. We determine this strategy for the mean-field version of the model and show that it amounts to supervising the values of spins (pixels) that do not agree with the sign of the average magnetization. The strategy leads to a transparent analytical expression for the minimal Bayesian risk, and shows that there is a maximal number of pixels beyond of which the supervision is useless. We show numerically that this strategy applies for two-dimensional images away from the critical regime. Within this regime the strategy is outperformed by its local (adaptive) version, which supervises pixels that do not agree with their Bayesian estimate. We show on transparent examples how active supervising can be essential in recovering noise-corrupted images and advocate for a wider usage of active methods in image restoration.

Relating Zipf's law to textual information

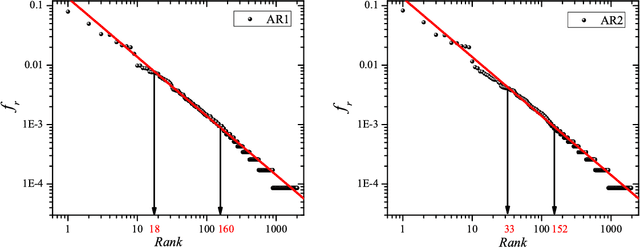
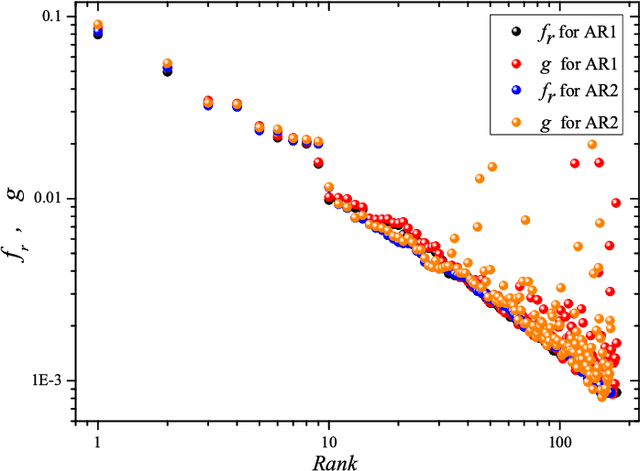
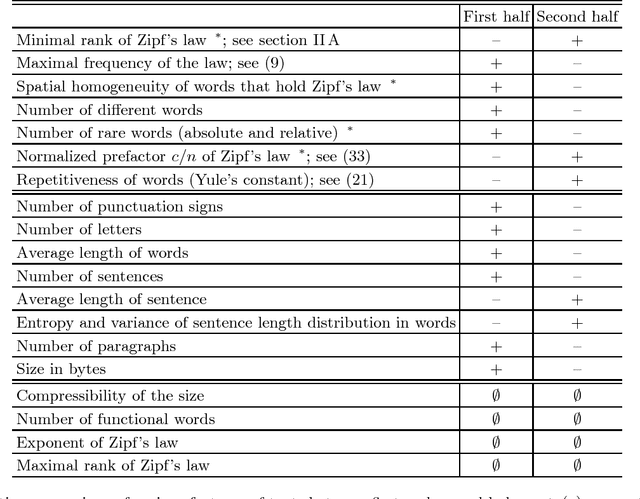
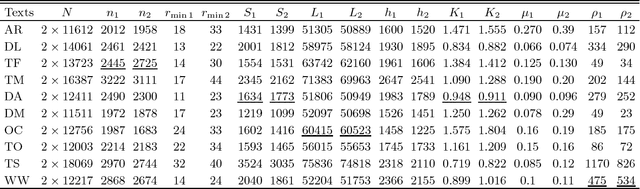
Zipf's law is the main regularity of quantitative linguistics. Despite of many works devoted to foundations of this law, it is still unclear whether it is only a statistical regularity, or it has deeper relations with information-carrying structures of the text. This question relates to that of distinguishing a meaningful text (written in an unknown system) from a meaningless set of symbols that mimics statistical features of a text. Here we contribute to resolving these questions by comparing features of the first half of a text (from the beginning to the middle) to its second half. This comparison can uncover hidden effects, because the halves have the same values of many parameters (style, genre, author's vocabulary {\it etc}). In all studied texts we saw that for the first half Zipf's law applies from smaller ranks than in the second half, i.e. the law applies better to the first half. Also, words that hold Zipf's law in the first half are distributed more homogeneously over the text. These features do allow to distinguish a meaningful text from a random sequence of words. Our findings correlate with a number of textual characteristics that hold in most cases we studied: the first half is lexically richer, has longer and less repetitive words, more and shorter sentences, more punctuation signs and more paragraphs. These differences between the halves indicate on a higher hierarchic level of text organization that so far went unnoticed in text linguistics. They relate the validity of Zipf's law to textual information. A complete description of this effect requires new models, though one existing model can account for some of its aspects.

Stochastic model for phonemes uncovers an author-dependency of their usage

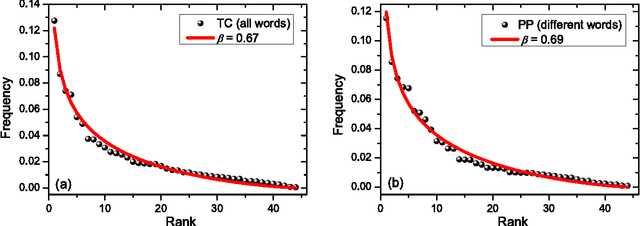
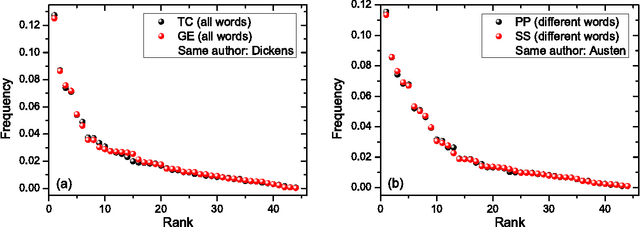
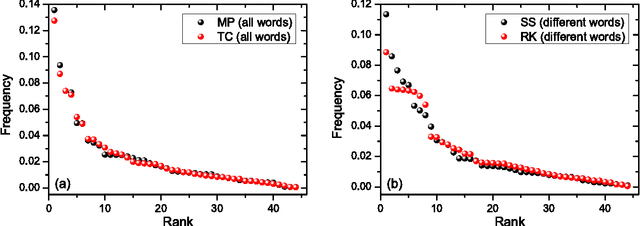
We study rank-frequency relations for phonemes, the minimal units that still relate to linguistic meaning. We show that these relations can be described by the Dirichlet distribution, a direct analogue of the ideal-gas model in statistical mechanics. This description allows us to demonstrate that the rank-frequency relations for phonemes of a text do depend on its author. The author-dependency effect is not caused by the author's vocabulary (common words used in different texts), and is confirmed by several alternative means. This suggests that it can be directly related to phonemes. These features contrast to rank-frequency relations for words, which are both author and text independent and are governed by the Zipf's law.

Active Inference for Binary Symmetric Hidden Markov Models

We consider active maximum a posteriori (MAP) inference problem for Hidden Markov Models (HMM), where, given an initial MAP estimate of the hidden sequence, we select to label certain states in the sequence to improve the estimation accuracy of the remaining states. We develop an analytical approach to this problem for the case of binary symmetric HMMs, and obtain a closed form solution that relates the expected error reduction to model parameters under the specified active inference scheme. We then use this solution to determine most optimal active inference scheme in terms of error reduction, and examine the relation of those schemes to heuristic principles of uncertainty reduction and solution unicity.

Comparative Analysis of Viterbi Training and Maximum Likelihood Estimation for HMMs

We present an asymptotic analysis of Viterbi Training (VT) and contrast it with a more conventional Maximum Likelihood (ML) approach to parameter estimation in Hidden Markov Models. While ML estimator works by (locally) maximizing the likelihood of the observed data, VT seeks to maximize the probability of the most likely hidden state sequence. We develop an analytical framework based on a generating function formalism and illustrate it on an exactly solvable model of HMM with one unambiguous symbol. For this particular model the ML objective function is continuously degenerate. VT objective, in contrast, is shown to have only finite degeneracy. Furthermore, VT converges faster and results in sparser (simpler) models, thus realizing an automatic Occam's razor for HMM learning. For more general scenario VT can be worse compared to ML but still capable of correctly recovering most of the parameters.

Phase Transitions in Community Detection: A Solvable Toy Model

Recently, it was shown that there is a phase transition in the community detection problem. This transition was first computed using the cavity method, and has been proved rigorously in the case of $q=2$ groups. However, analytic calculations using the cavity method are challenging since they require us to understand probability distributions of messages. We study analogous transitions in so-called "zero-temperature inference" model, where this distribution is supported only on the most-likely messages. Furthermore, whenever several messages are equally likely, we break the tie by choosing among them with equal probability. While the resulting analysis does not give the correct values of the thresholds, it does reproduce some of the qualitative features of the system. It predicts a first-order detectability transition whenever $q > 2$, while the finite-temperature cavity method shows that this is the case only when $q > 4$. It also has a regime analogous to the "hard but detectable" phase, where the community structure can be partially recovered, but only when the initial messages are sufficiently accurate. Finally, we study a semisupervised setting where we are given the correct labels for a fraction $\rho$ of the nodes. For $q > 2$, we find a regime where the accuracy jumps discontinuously at a critical value of $\rho$.

Explaining Zipf's Law via Mental Lexicon

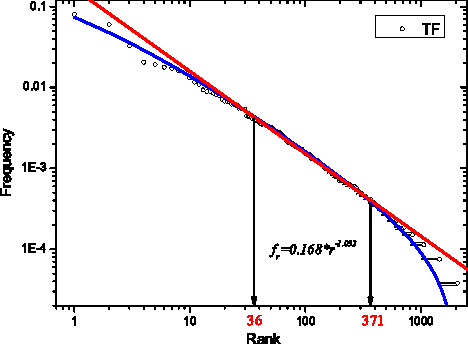
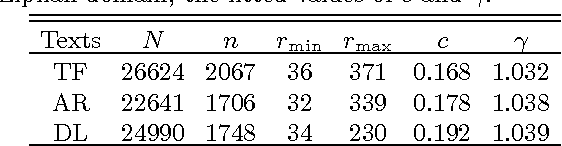
The Zipf's law is the major regularity of statistical linguistics that served as a prototype for rank-frequency relations and scaling laws in natural sciences. Here we show that the Zipf's law -- together with its applicability for a single text and its generalizations to high and low frequencies including hapax legomena -- can be derived from assuming that the words are drawn into the text with random probabilities. Their apriori density relates, via the Bayesian statistics, to general features of the mental lexicon of the author who produced the text.