Optimal alphabet for single text compression

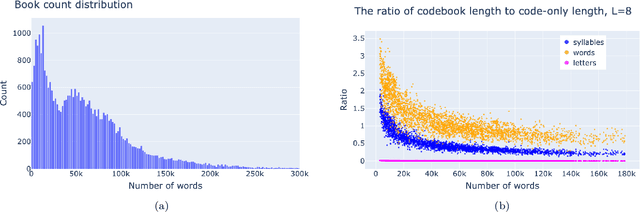
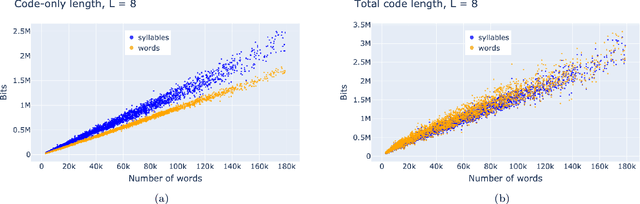
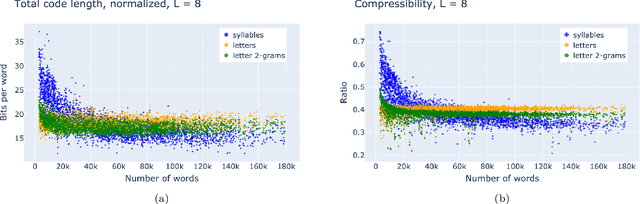
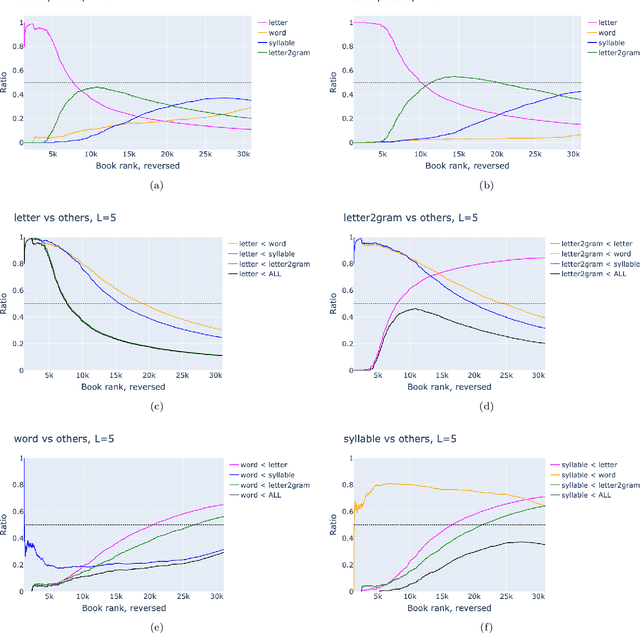
A text can be viewed via different representations, i.e. as a sequence of letters, n-grams of letters, syllables, words, and phrases. Here we study the optimal noiseless compression of texts using the Huffman code, where the alphabet of encoding coincides with one of those representations. We show that it is necessary to account for the codebook when compressing a single text. Hence, the total compression comprises of the optimally compressed text -- characterized by the entropy of the alphabet elements -- and the codebook which is text-specific and therefore has to be included for noiseless (de)compression. For texts of Project Gutenberg the best compression is provided by syllables, i.e. the minimal meaning-expressing element of the language. If only sufficiently short texts are retained, the optimal alphabet is that of letters or 2-grams of letters depending on the retained length.