Active image restoration
Paper and Code
Sep 22, 2018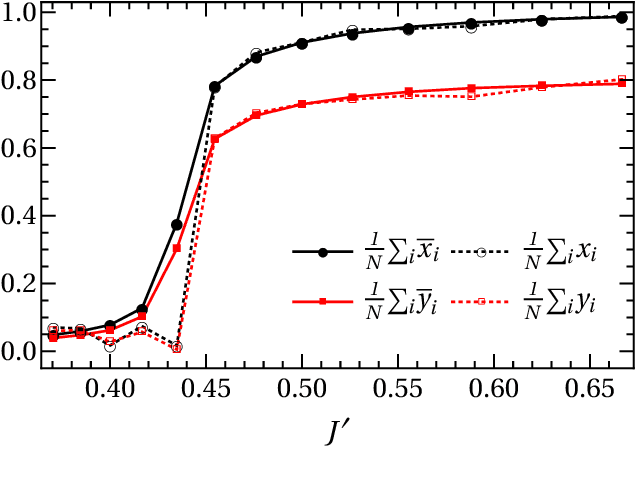


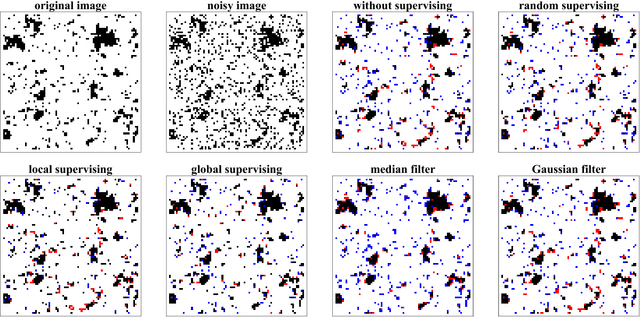
We study active restoration of noise-corrupted images generated via the Gibbs probability of an Ising ferromagnet in external magnetic field. Ferromagnetism accounts for the prior expectation of data smoothness, i.e. a positive correlation between neighbouring pixels (Ising spins), while the magnetic field refers to the bias. The restoration is actively supervised by requesting the true values of certain pixels after a noisy observation. This additional information improves restoration of other pixels. The optimal strategy of active inference is not known for realistic (two-dimensional) images. We determine this strategy for the mean-field version of the model and show that it amounts to supervising the values of spins (pixels) that do not agree with the sign of the average magnetization. The strategy leads to a transparent analytical expression for the minimal Bayesian risk, and shows that there is a maximal number of pixels beyond of which the supervision is useless. We show numerically that this strategy applies for two-dimensional images away from the critical regime. Within this regime the strategy is outperformed by its local (adaptive) version, which supervises pixels that do not agree with their Bayesian estimate. We show on transparent examples how active supervising can be essential in recovering noise-corrupted images and advocate for a wider usage of active methods in image restoration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge