Shengfeng Deng
Decoding fairness: a reinforcement learning perspective
Dec 20, 2024Abstract:Behavioral experiments on the ultimatum game (UG) reveal that we humans prefer fair acts, which contradicts the prediction made in orthodox Economics. Existing explanations, however, are mostly attributed to exogenous factors within the imitation learning framework. Here, we adopt the reinforcement learning paradigm, where individuals make their moves aiming to maximize their accumulated rewards. Specifically, we apply Q-learning to UG, where each player is assigned two Q-tables to guide decisions for the roles of proposer and responder. In a two-player scenario, fairness emerges prominently when both experiences and future rewards are appreciated. In particular, the probability of successful deals increases with higher offers, which aligns with observations in behavioral experiments. Our mechanism analysis reveals that the system undergoes two phases, eventually stabilizing into fair or rational strategies. These results are robust when the rotating role assignment is replaced by a random or fixed manner, or the scenario is extended to a latticed population. Our findings thus conclude that the endogenous factor is sufficient to explain the emergence of fairness, exogenous factors are not needed.
Transfer learning of phase transitions in percolation and directed percolation
Jan 06, 2022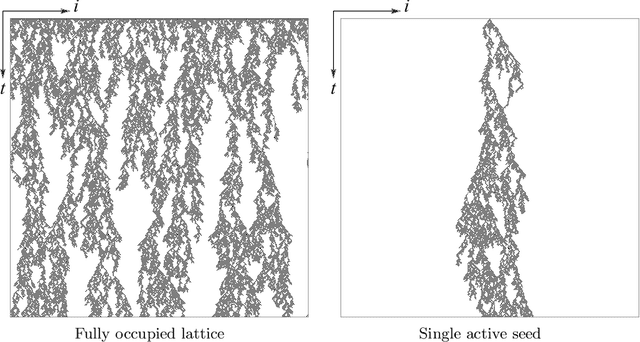
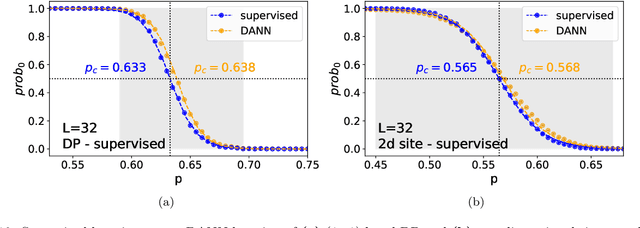

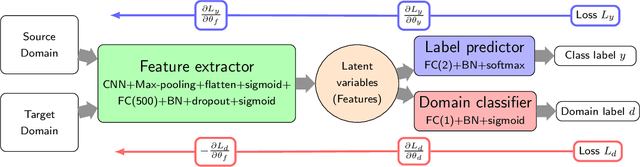
Abstract:The latest advances of statistical physics have shown remarkable performance of machine learning in identifying phase transitions. In this paper, we apply domain adversarial neural network (DANN) based on transfer learning to studying non-equilibrium and equilibrium phase transition models, which are percolation model and directed percolation (DP) model, respectively. With the DANN, only a small fraction of input configurations (2d images) needs to be labeled, which is automatically chosen, in order to capture the critical point. To learn the DP model, the method is refined by an iterative procedure in determining the critical point, which is a prerequisite for the data collapse in calculating the critical exponent $\nu_{\perp}$. We then apply the DANN to a two-dimensional site percolation with configurations filtered to include only the largest cluster which may contain the information related to the order parameter. The DANN learning of both models yields reliable results which are comparable to the ones from Monte Carlo simulations. Our study also shows that the DANN can achieve quite high accuracy at much lower cost, compared to the supervised learning.
Active image restoration
Sep 22, 2018


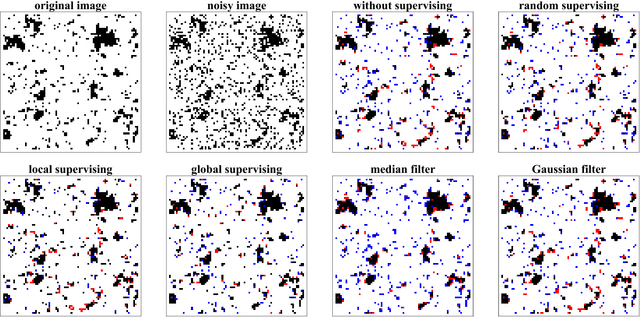
Abstract:We study active restoration of noise-corrupted images generated via the Gibbs probability of an Ising ferromagnet in external magnetic field. Ferromagnetism accounts for the prior expectation of data smoothness, i.e. a positive correlation between neighbouring pixels (Ising spins), while the magnetic field refers to the bias. The restoration is actively supervised by requesting the true values of certain pixels after a noisy observation. This additional information improves restoration of other pixels. The optimal strategy of active inference is not known for realistic (two-dimensional) images. We determine this strategy for the mean-field version of the model and show that it amounts to supervising the values of spins (pixels) that do not agree with the sign of the average magnetization. The strategy leads to a transparent analytical expression for the minimal Bayesian risk, and shows that there is a maximal number of pixels beyond of which the supervision is useless. We show numerically that this strategy applies for two-dimensional images away from the critical regime. Within this regime the strategy is outperformed by its local (adaptive) version, which supervises pixels that do not agree with their Bayesian estimate. We show on transparent examples how active supervising can be essential in recovering noise-corrupted images and advocate for a wider usage of active methods in image restoration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge