Stochastic model for phonemes uncovers an author-dependency of their usage
Paper and Code
Mar 20, 2016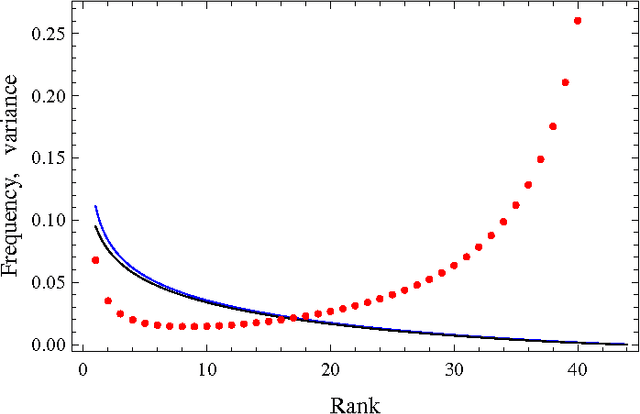
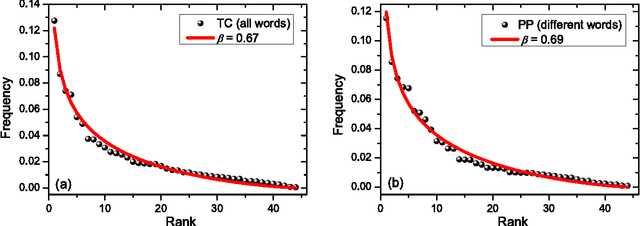
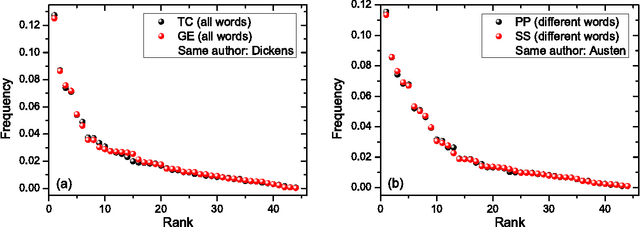
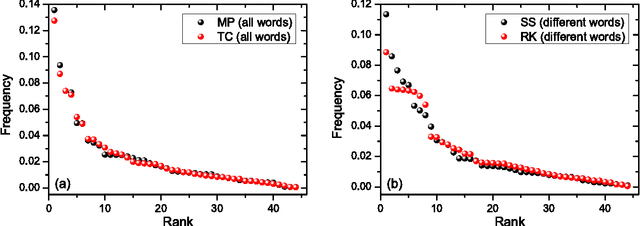
We study rank-frequency relations for phonemes, the minimal units that still relate to linguistic meaning. We show that these relations can be described by the Dirichlet distribution, a direct analogue of the ideal-gas model in statistical mechanics. This description allows us to demonstrate that the rank-frequency relations for phonemes of a text do depend on its author. The author-dependency effect is not caused by the author's vocabulary (common words used in different texts), and is confirmed by several alternative means. This suggests that it can be directly related to phonemes. These features contrast to rank-frequency relations for words, which are both author and text independent and are governed by the Zipf's law.
* PLoS ONE 11(4): e0152561 (2016) * 16 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge