Explaining Zipf's Law via Mental Lexicon
Paper and Code
Feb 18, 2013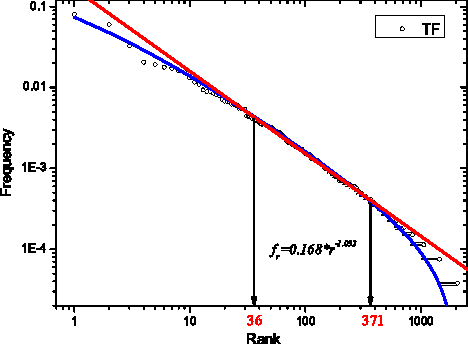
The Zipf's law is the major regularity of statistical linguistics that served as a prototype for rank-frequency relations and scaling laws in natural sciences. Here we show that the Zipf's law -- together with its applicability for a single text and its generalizations to high and low frequencies including hapax legomena -- can be derived from assuming that the words are drawn into the text with random probabilities. Their apriori density relates, via the Bayesian statistics, to general features of the mental lexicon of the author who produced the text.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge