Q. A. Wang
Rank-frequency relation for Chinese characters
Jan 26, 2014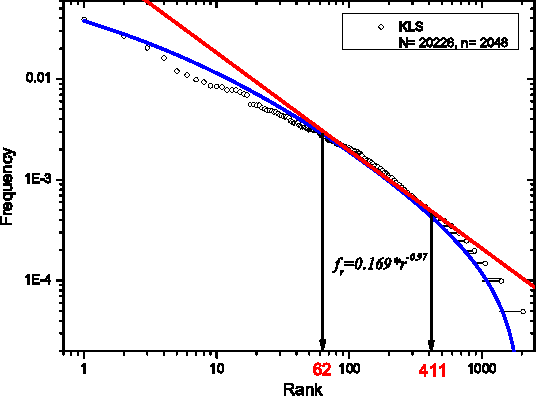
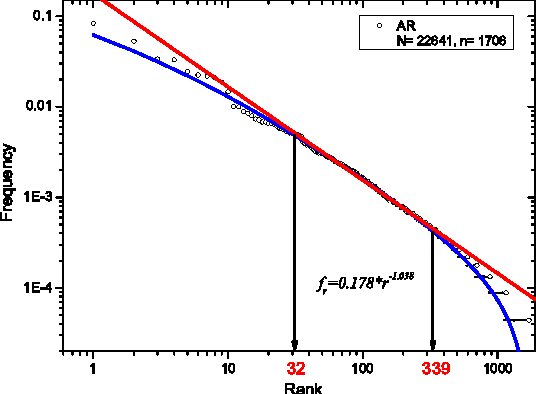
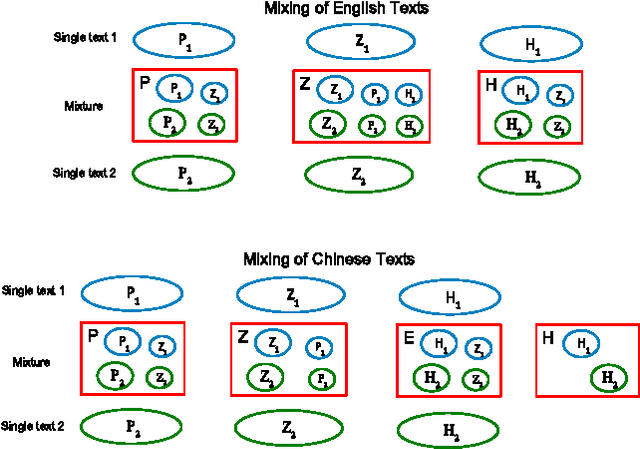
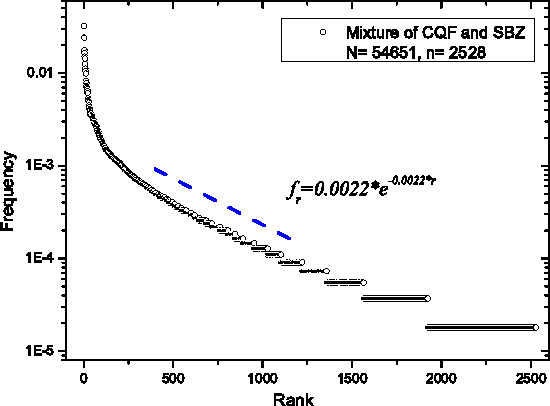
Abstract:We show that the Zipf's law for Chinese characters perfectly holds for sufficiently short texts (few thousand different characters). The scenario of its validity is similar to the Zipf's law for words in short English texts. For long Chinese texts (or for mixtures of short Chinese texts), rank-frequency relations for Chinese characters display a two-layer, hierarchic structure that combines a Zipfian power-law regime for frequent characters (first layer) with an exponential-like regime for less frequent characters (second layer). For these two layers we provide different (though related) theoretical descriptions that include the range of low-frequency characters (hapax legomena). The comparative analysis of rank-frequency relations for Chinese characters versus English words illustrates the extent to which the characters play for Chinese writers the same role as the words for those writing within alphabetical systems.
* To appear in European Physical Journal B (EPJ B), 2014 (22 pages, 7 figures)
Explaining Zipf's Law via Mental Lexicon
Feb 18, 2013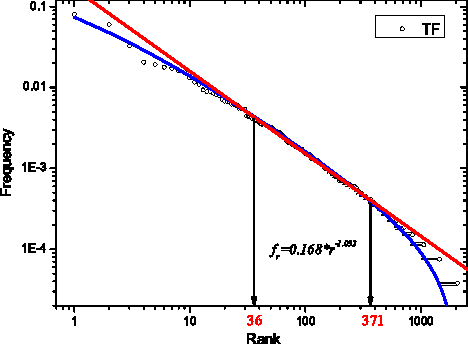
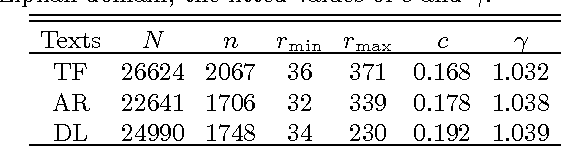
Abstract:The Zipf's law is the major regularity of statistical linguistics that served as a prototype for rank-frequency relations and scaling laws in natural sciences. Here we show that the Zipf's law -- together with its applicability for a single text and its generalizations to high and low frequencies including hapax legomena -- can be derived from assuming that the words are drawn into the text with random probabilities. Their apriori density relates, via the Bayesian statistics, to general features of the mental lexicon of the author who produced the text.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge