Resolution of Simpson's paradox via the common cause principle

Simpson's paradox is an obstacle to establishing a probabilistic association between two events $a_1$ and $a_2$, given the third (lurking) random variable $B$. We focus on scenarios when the random variables $A$ (which combines $a_1$, $a_2$, and their complements) and $B$ have a common cause $C$ that need not be observed. Alternatively, we can assume that $C$ screens out $A$ from $B$. For such cases, the correct association between $a_1$ and $a_2$ is to be defined via conditioning over $C$. This set-up generalizes the original Simpson's paradox. Now its two contradicting options simply refer to two particular and different causes $C$. We show that if $B$ and $C$ are binary and $A$ is quaternary (the minimal and the most widespread situation for valid Simpson's paradox), the conditioning over any binary common cause $C$ establishes the same direction of the association between $a_1$ and $a_2$ as the conditioning over $B$ in the original formulation of the paradox. Thus, for the minimal common cause, one should choose the option of Simpson's paradox that assumes conditioning over $B$ and not its marginalization. For tertiary (unobserved) common causes $C$ all three options of Simpson's paradox become possible (i.e. marginalized, conditional, and none of them), and one needs prior information on $C$ to choose the right option.

The most likely common cause

The common cause principle for two random variables $A$ and $B$ is examined in the case of causal insufficiency, when their common cause $C$ is known to exist, but only the joint probability of $A$ and $B$ is observed. As a result, $C$ cannot be uniquely identified (the latent confounder problem). We show that the generalized maximum likelihood method can be applied to this situation and allows identification of $C$ that is consistent with the common cause principle. It closely relates to the maximum entropy principle. Investigation of the two binary symmetric variables reveals a non-analytic behavior of conditional probabilities reminiscent of a second-order phase transition. This occurs during the transition from correlation to anti-correlation in the observed probability distribution. The relation between the generalized likelihood approach and alternative methods, such as predictive likelihood and the minimum common cause entropy, is discussed. The consideration of the common cause for three observed variables (and one hidden cause) uncovers causal structures that defy representation through directed acyclic graphs with the Markov condition.

Maximum Entropy competes with Maximum Likelihood

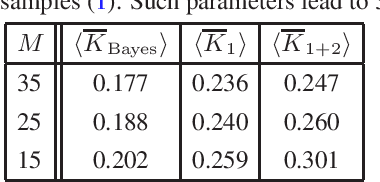
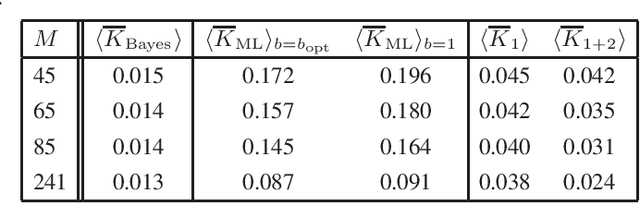
Maximum entropy (MAXENT) method has a large number of applications in theoretical and applied machine learning, since it provides a convenient non-parametric tool for estimating unknown probabilities. The method is a major contribution of statistical physics to probabilistic inference. However, a systematic approach towards its validity limits is currently missing. Here we study MAXENT in a Bayesian decision theory set-up, i.e. assuming that there exists a well-defined prior Dirichlet density for unknown probabilities, and that the average Kullback-Leibler (KL) distance can be employed for deciding on the quality and applicability of various estimators. These allow to evaluate the relevance of various MAXENT constraints, check its general applicability, and compare MAXENT with estimators having various degrees of dependence on the prior, viz. the regularized maximum likelihood (ML) and the Bayesian estimators. We show that MAXENT applies in sparse data regimes, but needs specific types of prior information. In particular, MAXENT can outperform the optimally regularized ML provided that there are prior rank correlations between the estimated random quantity and its probabilities.

Observational nonidentifiability, generalized likelihood and free energy

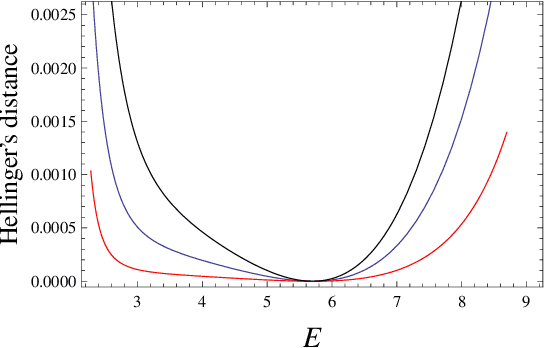
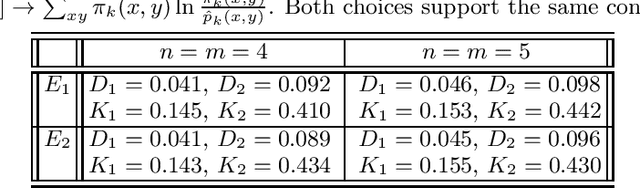
We study the parameter estimation problem in mixture models with observational nonidentifiability: the full model (also containing hidden variables) is identifiable, but the marginal (observed) model is not. Hence global maxima of the marginal likelihood are (infinitely) degenerate and predictions of the marginal likelihood are not unique. We show how to generalize the marginal likelihood by introducing an effective temperature, and making it similar to the free energy. This generalization resolves the observational nonidentifiability, since its maximization leads to unique results that are better than a random selection of one degenerate maximum of the marginal likelihood or the averaging over many such maxima. The generalized likelihood inherits many features from the usual likelihood, e.g. it holds the conditionality principle, and its local maximum can be searched for via suitably modified expectation-maximization method. The maximization of the generalized likelihood relates to entropy optimization.

Rank-frequency relation for Chinese characters

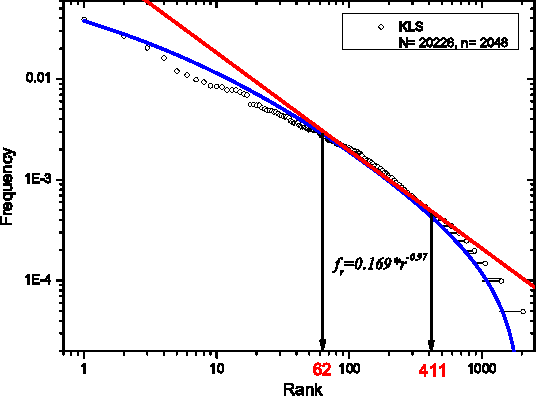
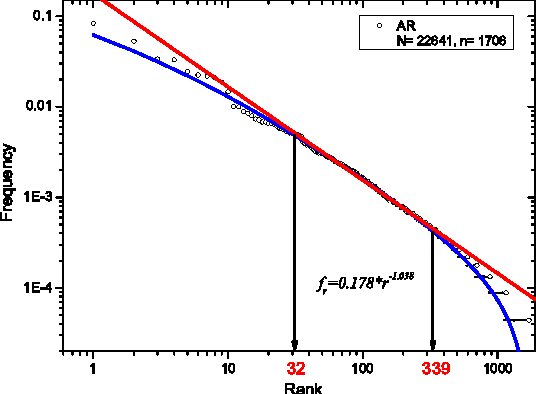
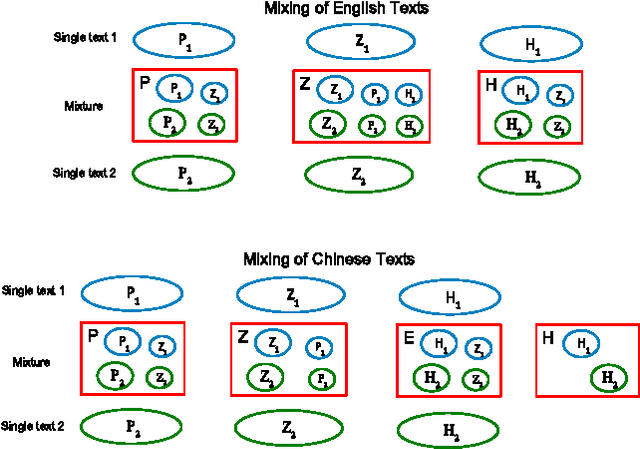
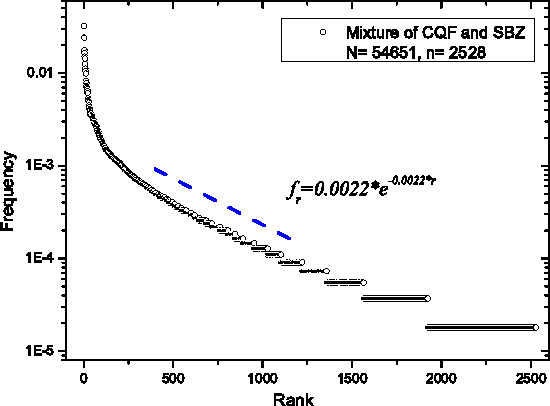
We show that the Zipf's law for Chinese characters perfectly holds for sufficiently short texts (few thousand different characters). The scenario of its validity is similar to the Zipf's law for words in short English texts. For long Chinese texts (or for mixtures of short Chinese texts), rank-frequency relations for Chinese characters display a two-layer, hierarchic structure that combines a Zipfian power-law regime for frequent characters (first layer) with an exponential-like regime for less frequent characters (second layer). For these two layers we provide different (though related) theoretical descriptions that include the range of low-frequency characters (hapax legomena). The comparative analysis of rank-frequency relations for Chinese characters versus English words illustrates the extent to which the characters play for Chinese writers the same role as the words for those writing within alphabetical systems.