Observational nonidentifiability, generalized likelihood and free energy
Paper and Code
Feb 18, 2020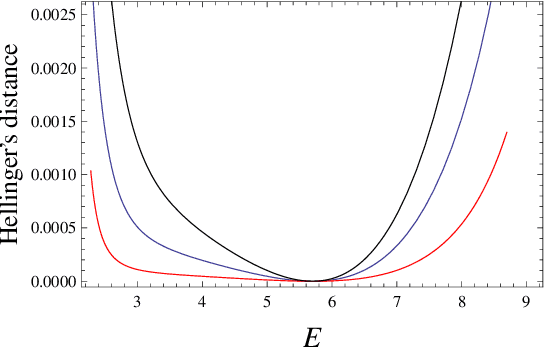
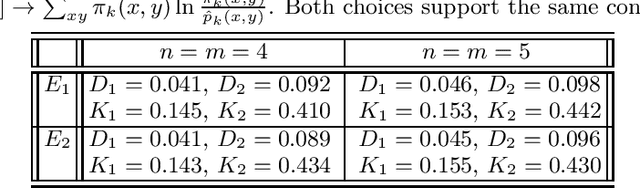

We study the parameter estimation problem in mixture models with observational nonidentifiability: the full model (also containing hidden variables) is identifiable, but the marginal (observed) model is not. Hence global maxima of the marginal likelihood are (infinitely) degenerate and predictions of the marginal likelihood are not unique. We show how to generalize the marginal likelihood by introducing an effective temperature, and making it similar to the free energy. This generalization resolves the observational nonidentifiability, since its maximization leads to unique results that are better than a random selection of one degenerate maximum of the marginal likelihood or the averaging over many such maxima. The generalized likelihood inherits many features from the usual likelihood, e.g. it holds the conditionality principle, and its local maximum can be searched for via suitably modified expectation-maximization method. The maximization of the generalized likelihood relates to entropy optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge