Paolo P. Mazza
Statistical Inference of Minimally Complex Models
Aug 02, 2020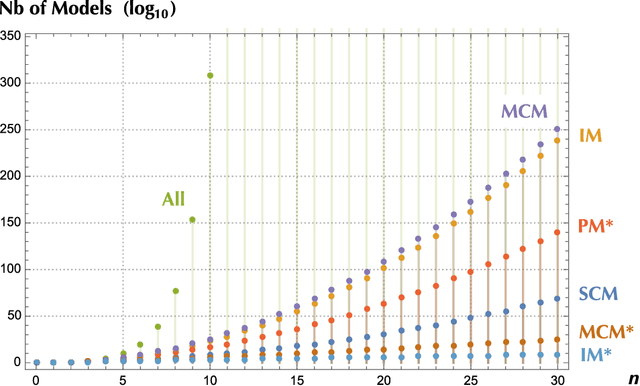
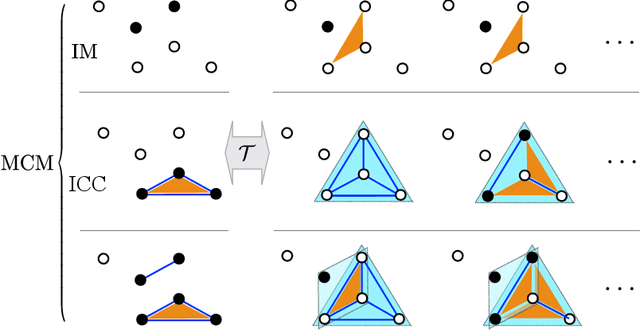
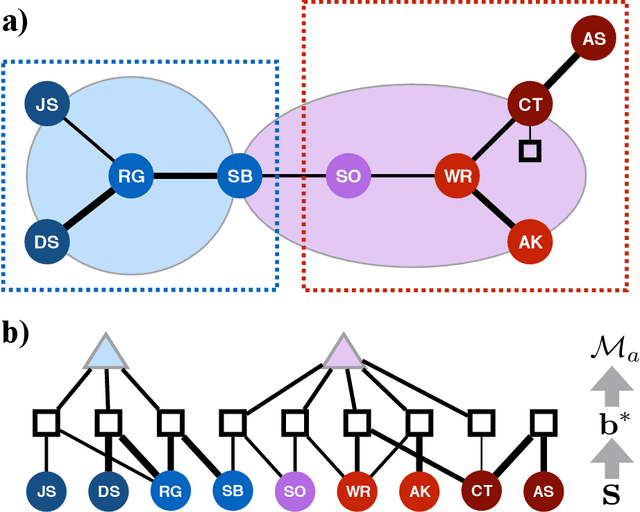
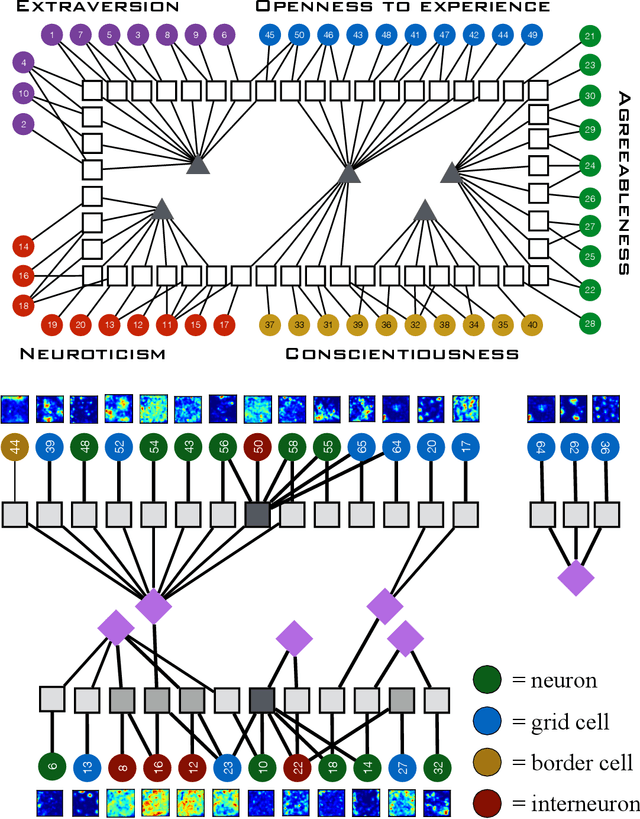
Abstract:Finding the best model that describes a high dimensional dataset, is a daunting task. For binary data, we show that this becomes feasible, if the search is restricted to simple models. These models -- that we call Minimally Complex Models (MCMs) -- are simple because they are composed of independent components of minimal complexity, in terms of description length. Simple models are easy to infer and to sample from. In addition, model selection within the MCMs' class is invariant with respect to changes in the representation of the data. They portray the structure of dependencies among variables in a simple way. They provide robust predictions on dependencies and symmetries, as illustrated in several examples. MCMs may contain interactions between variables of any order. So, for example, our approach reveals whether a dataset is appropriately described by a pairwise interaction model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge